Глава 3. Биоэлектрические потенциалы

Одна из важнейших функций биологической мембраны - генерация и передача биопотенциалов. Это явление лежит в основе возбудимости клеток, регуляции внутриклеточных процессов, работы нервной системы, регуляции мышечного сокращения, рецепции. В медицине на исследование электрических полей, созданных биопотенциалами органов и тканей, основаны диагностические методы: электрокардиография, электроэнцефалография, электромиография и другие. Практикуется и лечебное воздействие на ткани и органы внешними электрическими импульсами при электростимуляции.

В процессе жизнедеятельности в клетках и тканях могут возникать разности электрических потенциалов: Δj

1) окислительно-восстановительные потенциалы - вследствие переноса электронов от одних молекул к другим;

2) мембранные - вследствие градиента концентрации ионов и переноса ионов через мембрану.

Биопотенциалы, регистрируемые в организме, — это в основном мембранные потенциалы.

Мембранным потенциалом называется разность потенциалов между внутренней (цитоплазматической) и наружной поверхностями мембраны:

j_м = j_нар- j_вн. (1)

Прогресс в исследовании биопотенциалов обусловлен:

1) разработкой микроэлектродного метода внутриклеточного измерения потенциалов;

2) созданием специальных усилителей биопотенциалов (УПТ);

3) выбором удачных объектов исследования крупных клеток и среди них гигантского аксона кальмара. Диаметр аксона кальмара достигает 0,5 мм, что в 100 - 1000 больше, чем диаметр аксонов позвоночных животных, в том числе человека. Гигантские, в сравнении с позвоночными, размеры аксона -этого проворного и ловкого головоногого моллюска - имеют большое физиологическое значение -обеспечивают быструю передачу нервного импульса по нервному волокну.

Для биофизики гигантский аксон кальмара послужил великолепным модельным объектом для изучения биопотенциалов. В гигантский аксон кальмара можно ввести микроэлектрод, не нанеся аксону значительных повреждений.

Стеклянный микроэлектрод представляет собой стеклянную микропипетку с оттянутым очень тонким кончиком (рис.17 ).

Металлический электрод такой толщины пластичен и не может проколоть клеточную мембрану, кроме того он поляризуется. Для исключения поляризации электрода используются не­поляризующиеся электроды, например серебряная проволока, покрытая солью AgCL В раствор КС1 или NaCl (желатинизированный агар-агаром), заполняющий микроэлектрод.

Второй электрод - электрод сравнения - располагается в растворе у наружной поверхности клетки. Регистрирующее устройство Р, содержащее усилитель постоянного тока, измеряет мембранный потенциал:

Рис.17. Микроэлектродный метод измерения биопотенциалов

а - стеклянная микропипетка; б - стеклянный микроэлектрод;

в - схема регистрации мембранного потенциала

Микроэлектродный метод дал возможность измерить биопотенциалы не только на гигантском аксоне кальмара, но и на клетках нормальных размеров: нервных волокнах других животных, клетках скелетных мышц, клетках миокарда и других.

Мембранные потенциалы подразделяются на потенциалы покоя и потенциалы действия.

и 10. Потенциал покоя в клетках

Потенциал покоя - стационарная разность электрических потенциалов, регистрируемая между внутренней и наружной поверхностями мембраны в невозбужденном состоянии.

Потенциал покоя определяется разной концентрацией ионов по разные стороны мембраны и диффузией ионов через мембрану.

Если концентрация какого-либо иона внутри клетки С_вн отлична от концентрации этого иона снаружи С_нар и мембрана проница­ема для этого иона, возникает поток заряженных частиц через мембрану, вследствие чего нарушается электрическая нейтральность системы, образуется разность потенциалов внутри и снаружи клетки j_м = j_нар- j_вн которая будет препятствовать дальнейшему перемещению ионов через мембрану. При установлении равновесия выравниваются значения электрохимических потенциалов по разные стороны мембраны: m_вн = m_нар.

Так как m = m₀ + RTlnC + ZFj, то

RTlnC_вн + ZFj_вн = RTlnC_нар + ZFj_нар

Отсюдалегко получить формулу Нернста для равновесного мембранного потенциала

j_м = j_нар- j_вн = - RT/ZF´ln(C_вн/С_нар)

Если мембранный потенциал обусловлен переносом ионов К⁺,для которого [К⁺]_вн > [К⁺]_нар и Z = +1, равновесный мембранный потенциал

.

Для ионов Na⁺:[Na⁺]_вн<[Na⁺]_нар, Z = +1,

>0,

Если в формуле Нернста перейти от натурального логарифма к десятичному, то для положительного одновалентного иона (Z = +1)

,

Примем температуру Т=300 К, тогда

.

.

Примем в формуле Нернста С_вн/С_нар≈100, что по порядку величины соответствуют экспериментальным данным для калия:

lg , и мембранный потенциал

= 0,06∙2В = 0,12В = 120мВ,

что несколько больше модуля экспериментально измеренных значений потенциала покоя, и, пользуясь формулами электростатики, оценим, какое количество ионов должно перейти из цитоплазмы в неклеточную среду, чтобы создать такую разность потенциалов. Радиус клетки r = 10 мкм = 10^-5 м. Удельная электроемкость мембраны (электроемкость на единицу площади) С_уд=10^-2 Ф/м². Площадь мембраны 4πr² ≈ 4π∙10^-10м² ≈10^-9м². Тогда электроемкость мембраны

C=C_уд∙S≈10^-2 ∙10^-9 м².

Абсолютная величина заряда каждого знака на поверхности мембраны, если ее представить себе как конденсатор,

,

что соответствует

Объем клетки

V= .

Изменение концентрации ионов в клетке вследствие выхода из клетки 10^-17 моль ионов составит

∆С≈ .

Это ничтожное изменение концентрации по сравнению с изменением концентрации ионов калия внутри клетки, составляет всего 10^-4% от концентрации калия внутри клетки. Таким образом, чтобы создать равновесный нернстовский мембранный потенциал, через мембрану должно пройти пренебрежимо малое количество ионов по сравнению с общим их количеством в клетке.

Таким образом, потенциал покоя на самом деле ближе к потенциалу, рассчитанному по формуле Нернста для К⁺.Вместе с тем, обращает на себя внимание значительное расхождение экспериментальных и теоретических значений. Причины расхождения в том, что не учтена проницаемость мембраны для других ионов. Одновременная диффузия через мембрану ионов К⁺, Na⁺ и С1^- учитывается уравнением Гольдмана.

Уравнение Гольдмана можно вывести из уравнения Нернста-Планка.

.

Преобразуем это уравнение:

URT=D согласно соотношению Эйнштейна. Примем так называемое приближение постоянного поля Гольдмана. Будем считать напряженность электрического поля в мембране постоянной и равной среднему значению градиента потенциала:

где l – толщина мембраны.

Получим для плотности ионного потока через мембрану:

Обозначим Запишем

Разделим переменные:

Проинтегрируем левую часть дифференциального уравнения в пределах от 0 до 1, а правую от С_нар=КС_нар до С_вн=КС_вн (где К – коэффициент распределения)

Получим:

После потенциирования

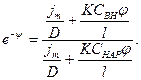
Выразим отсюда:

Учитывая, что , получим:

В стационарном случае, когда разность потенциалов - мембранный потенциал - тормозит дальнейший перенос ионов через мембрану, суммарный поток различных ионов становится равным нулю:

j_K+ + j_Na+ - j_Cl- = 0

Перед j. стоит знак минус, учитывающий отрицательный заряд иона хлора. Однако, так как в создании мембранного потенциала участвуют различные ионы, равновесие при этом не наступает, потоки различных ионов не равны нулю по отдельности. Если учесть только потоки j_K+ и j_Na+, то j_K++j_Na+=0, или j_K= - j_Na+ и, подставив, получим:

и

.

Отсюда:

Поскольку,

, (Z =1),

то

Если учесть еще и поток ионов С1^-, то, повторив предыдущие рассуждения, можно получить уравнение для мембранного потенциала, созданного потоками через мембрану трех видов ионов, уравнение Гольдмана:

В числителе выражения, стоящего под знаком логарифма, представлены концентрации [К⁺]_ВН, [Na⁺]_BH, но [С1^-]_НАР, а в знаменателе - [К⁺]_НАР, [Na⁺]_HАР, но [С1^-]_ВН, так как ионы хлора отрицательно заряжены.

В состоянии покоя проницаемость мембраны для ионов К⁺ значительно больше, чем для Na⁺, и больше, чем для С1^-:

P_K>>P_Na, P_K>P_Na.

Для аксона кальмара, например,

P_K:P_Na:P_Cl=1:0,04:0,45.

Переписав уравнение Гольдмана в виде:

,

в случае, когда проницаемость мембраны для ионов натрия и хлора значительно меньше проницаемости для калия:

P_Na << P_K, P_Cl<< P_K,

Таким образом, уравнение Нернста - частный случай уравнения Гольдмана.

Мембранный потенциал, рассчитанный по уравнению Гольдмана, оказался по абсолютной величине меньше мембранного потенциала, рассчитанного по формуле Нернста» ближе к экспериментальным его значениям в крупных клетках. И формула Нернста, и уравнение Гольдмана не учитывают активного транспорта ионов через мембрану, наличия в мембранах электрогенных (вызывающих разделение зарядов, а следовательно и возникновение разности потенциалов) ионных насосов, играющих важную роль в поддержании ионного равновесия в мелких клетках. В цитоплазматической мембране работают К⁺-Nа⁺-АТФазы, перекачивающие калий внутрь клетки, а натрий из клетки. С учетом работы электрогенных ионных насосов для мембранного потенциала было получено уравнение Томаса:

,

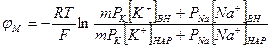где m - отношение количества ионов натрия к количеству ионов калия, перекачиваемых ионными насосами через мембрану. Чаще всего К⁺-Ка⁺-АТФаза работает в режиме, когда m = 3/2, m всегда больше 1. (Нет ионных насосов, перекачивающих Сl, поэтому в уравнении Томаса отсутствуют члены Р _Сl [ Сl^- ].)

Коэффициент m > 1 усиливает вклад градиента концентрации калия в создание мембранного потенциала, поэтому мембранный потенциал, рассчитанный по Томасу, больше по абсолютной величине, чем мембранный потенциал, рассчитанный по Гольману, и дает совпадение с экспериментальными значениями для мелких клеток.

Нарушение биоэнергетических процессов в клетке и работы K⁺-Na⁺-АТФазы приводит к уменьшению |φ_м|, в этом случае мембранный потенциал лучше описывается уравнением Гольдмана.

Повреждение клеточной мембраны приводит к повышению проницаемости клеточных мембран для всех ионов: к повышению и P_к, и P_Na, и P_сl Вследствие уменьшение различия проницаемостей абсолютное значение мембранного потенциала |φ_м| снижается.

Для сильно поврежденных клеток |φ_м| еще меньше, но сохраняется отрицательный мембранный потенциал |φ_м| за счет содержащихся в клетке полианионов - отрицательно заряженных белков, нуклеиновых кислот и других крупных молекул, не могущих проникнуть через мембрану (доннановский потенциал).

Потенциал действия

Посредством электрических нервных импульсов (потенциалов действия) в живом организме передается информация от рецепторов к нейронам мозга и от нейронов мозга к мышцам. Живой организм является полностью электрифицированной системой. Без электричества нет жизни.

Потенциал действия был открыт раньше потенциала покоя. Животное электричество известно давно. Разряды электрического угря (происходящие при напряжении до 600 В, с током около 60 А и длительностью порядка миллисекунды) использовались медициной еще в Древнем Риме для лечения подагры, головной боли, эпилепсии. Электрический нервный импульс открыл Луиджи Гальвани, профессор анатомии в г. Болонья. Результаты его электрофизиологических опытов изложены в книге "Трактат о силах электричества при мышечном движении" (1791 г.). Гальвани открыл, что мышечные сокращения конечностей препарированной лягушки могут вызваться электрическим импульсом и что сама живая система является источником электрического импульса. Великое открытие Гальвани сыграло выдающуюся роль в развитии физики, электротехники, электрохимии, физиологии, биофизикии и медицины. Однако, огромная популярность идей Гальвани привела к их профанациям, следы которых остались до нашего времени (гальванизация трупов, гальванизм прикосновений взглядов и т.д.), что вызывало недоверие к экспериментам Гальвани ученых-физиков. Младший современник Гальвани профессор физики Алессандро Вольта был яростым противником идеи животного электричества (за исключением особых случаев электрических рыб: электрического угря и электрического ската). В своих экспериментах он исключил биологический объект и показал, что электрический ток может быть получен при контакте набора металлов, разделенных электролитом (вольтов столб). Так был открыт химический источник тока (названный, однако, позже, в честь его научного противника гальваническим элементом).

В XIX веке утвердилось примитивное представление о распространении электрических токов по нервам, как по проводам. Однако Гельмгольцем (вторая половина XIX века) было показано, что скорость распространения нервного импульса составляет лишь 1-100 м/с, это значительно меньше, чем скорость распространения электрического импульса по проводам до 3 • 10⁸ м/с. Поэтому к концу XIX века гипотеза электрической природы нервного импульса была отвергнута большинством физиологов. Было выдвинуто предположение о распространении по нервным волокнам химической реакции. На самом деле, как было показано позже, медленное распространение электрического нервного импульса связано с медленной перезарядкой конденсаторов, которые представляют собой клеточные мембраны, через большие сопротивления. Постоянная времени перезарядки мембраны τ= RC велика, так как велики емкость мембраны (С) и сопротивление R нервного волокна.

То, что нервный импульс представляет собой импульс электрического тока, было доказано лишь к середине 20-го века, в основном в работах английского физиолога А. Ходжкина и его сотрудников. В1963 году Ходжкину, Хаксли и Иклсу была присуждена Нобелевская премия по медицине "за оперирование нервных клеток".

Потенциалом действия (ПД) называется электрический импульс, обусловленный изменением ионной проницаемости мембраны и связанный с распространением по нервам и мышцам волны возбуждения.

Опыты по исследованию потенциала действия проведены (в основном Ходжкиным и его сотрудниками) на гигантских аксона кальмара методом микроэлектродов с использованием высокоомных измерителей напряжения, а также методом меченых атомов. На риспоказаны схема опытов и результаты исследований.

В опытах по исследованию потенциала действия использовали два микроэлектрода, введенных в аксон. На первый микроэлектрод подается импульс с амплитудой V от генератора Г прямоугольных импульсов, меняющий мембранный потенциал. Мембранный потенциал измеряется при помощи второго микроэлектрода высокоомным регистратором напряжения Р.

Рис.18. Исследование потенциала действия:

а - схема опыта (Г - генератор импульсов, Р - регистратор напряжения); б - потенциал действия (φ^п_м - потенциал покоя, φ^рев_м - потенциал реверсии, φ^д_м - амплитуда потенциала действия, φ^пор_м – пороговый потенциал)

Возбуждающий импульс вызывает лишь на короткое время смещение мембранного потенциала, который быстро пропадает и восстанавливается потенциал покоя. В том случае, когда возбуждающий импульс смещается еще дальше в отрицательную сторону, он сопровождается гиперполяризацией мембраны. Также не формируется потенциал действия, когда возбуждающий импульс положительный (деполяризующий), но его амплитуда меньше порогового значения V_nop. Однако, если амплитуда положительного, деполяризующего импульса окажется больше значения V^nop, φ_м становится больше φ^пор_м и в мембране развивается процесс, в результате которого происходит резкое повышение мембранного потенциала и мембранный потенциал φ_м даже меняет свой знак - становится положительным (φ_вн>φ_нар).

Достигнув некоторого положительного значения φ^рев - потенциала реверсии, мембранный потенциал возвращается к значению потенциала покоя φ^п_м, совершив нечто вроде затухающего колебания. В нервных волокнах и скелетных мышцах длительность потенциала действия около 1 мс (а в сердечной мышце около 300 мс. После снятия возбуждения еще в течение 1 -3 мс в мембране наблюдаются некоторые остаточные явления, во время которых мембрана рефрактерна (невозбудима).

Новый деполяризующий потенциал V > V^nop может вызвать образование нового потенциала действия только после полного возвращения мембраны в состояние покоя. Причем амплитуда потенциала действия

не зависит от амплитуды деполяризующего потенциала (если только V > V^nop). Если в покое мембрана поляризована (потенциал цитоплазмы отрицателен по отношению к внеклеточной среде), то при возбуждении происходит деполяризация мембраны (потенциал внутри клетки положителен) и после снятия возбуждения происходит реполяризация мембраны.

Характерные свойства потенциала действия:

1) наличие порогового значения деполяризующего потенциала;

2) закон "все или ничего", то есть, если деполяризующий потенциал больше порогового, развивается потенциал действия, амплитуда которого не зависит от амплитуды возбуждающего импульса и нет потенциала действия, если амплитуда деполяризующего потенциала меньше пороговой;

3) есть период рефрактерности, невозбудимости мембраны во время развития потенциала действия и остаточных явлений после снятия возбуждения;

4) в момент возбуждения резко уменьшается сопротивление мембраны (у аксона кальмара от 0,1 Ом • м² в покое до 0,0025 Ом • м² при возбуждении).

Если обратиться к данным для значений равновесных нернстовских потенциалов, созданных различными ионами, естественно предположить, что положительный потенциал реверсии имеет натриевую природу, поскольку именно диффузия натрия создает положительную разность потенциалов между внутренней и наружной поверхностями мембраны.

Можно менять амплитуду импульса потенциала действия, изменяя концентрацию натрия в наружной среде. При уменьшении наружной концентрации натрия амплитуда потенциала действия уменьшается, так как меняется потенциал реверсии. Если из окружающей клетку среды полностью удалить натрий, потенциал действия вообще не возникает.

Опыты, проведенные с радиоактивным изотопом натрия, позволили установить, что при возбуждении проницаемость для натрия резко возрастает. Если в состоянии покоя соотношение коэффициентов проницаемости мембраны аксона кальмара для разных ионов:

P_K: P_Na: P_Cl = 1: 0,04: 0,45

то в состоянии возбуждения:

P_K: P_Na: P_Cl = 1: 20: 0,45

то есть, по сравнению с невозбужденным состоянием, при возбуждении коэффициент проницаемости для натрия возрастает в 500 раз.

Расчеты мембранного потенциала реверсии по уравнению Гольдмана, если в него подставить значения проницаемостей мембраны для возбужденного состояния, совпадают с экспериментальными данными.

Возбуждение мембраны описывается уравнениями Ходжкина-Хаксли. Одно из уравнений Ходжкина-Хаксли имеет вид:

,

где I_м - ток через мембрану, С_м - емкость мембраны, ∑I_i - сумма ионных токов через мембрану.

Электрический ток через мембрану складывается из ионных токов: ионов калия - I_k+, натрия - I_Na+ и других ионов, в том числе Сl, так называемого тока утечки I_k, а также емкостного тока. Емкостной ток обусловлен перезарядкой конденсатора, который представляет собой мембрана, перетеканием зарядов с одной ее поверхности на другую. Его величина определяется количеством заряда, перетекающего с одной обкладки на другую за единицу времени dq/dt, а поскольку заряд конденсатоpa q = С_м∆φ = С_мφ_м, то емкостной ток С_М . Полный мембранный ток

.

Согласно теории Ходжкина-Хаксли, возбуждение элемента мембраны связано с изменениями проводимости мембраны для ионов Na⁺ и К⁺: g_K и g_Na.

Проводимости мембраны сложным образом зависят от мембранного потенциала и времени.

Будем считать ток, направленный из клетки наружу в окружающий раствор положительным, а внутрь клетки из окружающего раствора - отрицательным.

Обнаружено, что, если поднять мембранный потенциал (φ_м выше порогового, сначала течет ток внутрь клетки, а затем из клетки наружу).

В экспериментах, проведенных Ходжкиным, Хаксли, Бейкером, Шоу, было доказано, что фаза I мембранного тока связана с потоком ионов натрия из окружающей среды (где концентрация натрия больше) в клетку (где она меньше), а фаза II объясняется вытеканием ионов калия из клетки наружу.

В своих опытах Ходжкин и Хаксли изменяли ионный состав окружающего раствора. Было обнаружено, что, если снаружи убирали натрий, первая фаза мембранного тока (ток внутрь клетки) пропадала. Следовательно, на самом деле, первая фаза развития потенциала действия связана с увеличением проницаемости мембраны для ионов натрия. Поток положительных частиц в клетку приводит к деполяризации мембраны - внутренняя ее поверхность заряжается положительно по отношению к наружной.

Во второй фазе резко увеличивается проницаемость мембраны для калия и из клетки наружу выходят положительно заряженные ионы калия, в то время как натриевый ток уменьшается.

Ионный механизм развития потенциала действия был окончательно доказан в решающем эксперименте Ходжкина, Бейкера и Шоу, в котором аксоплазму препарированного аксона заменили на наружный раствор, а ионный состав наружного раствора сделали таким же, как у нормальной аксоплазмы. При такой замене ионных составов изменила знак разность потенциалов на мембране. Теперь в покое внутренняя ее поверхность была заряжена положительно по отношению к наружной. А потенциал действия оказался отрицательным.

Выдвинута гипотеза, что селективное (избирательное) изменение ионной проницаемости возбужденной мембраны: сначала для Na⁺, а потом для К⁺ - объясняется тем, что в мембране имеются специальные ионные каналы. Существуют отдельно натриевые и калиевые каналы, которые открываются и закрываются во время прохождения через данный участок мембраны нервного импульса. В первой фазе - открываются натриевые каналы, во второй фазе - калиевые. Соответственно, сначала закрываются натриевые каналы, а затем калиевые. Открывание и закрывание ионных каналов вызывается изменением мембранного потенциала.

Одно из доказательств наличия в мембране ионных каналов -существование веществ, блокирующих ионные потоки через мембрану.

Так, содержащийся в рыбе фугу тетродотоксин блокирует поступление внутрь клетки натрия и, таким образом, нарушает передачу нервного импульса, что может привести к летальному исходу. Доказано, что тетродотоксин не влияет на проницаемость клетки для калия, значит, ионы натрия и калия на самом деле проходят через разные каналы.

Из-за своего специфического строения молекулы тетродотоксина, по-видимому, застревают в натриевых каналах. Подсчитав число застрявших в мембране молекул тетродотоксина, удалось определить количество натриевых каналов. В разных нервных волокнах позвоночных оно было разным — от 3 до 75 каналов на один квадратный микрометр площади мембраны (для сравнения количество молекул фосфолипидов ≈ 2 • 10⁶ 1/мкм²).

Был обнаружен и специфический ингибитор калиевых каналов - тетраэтиламмоний.

Если обработать мембрану тетродотоксином, блокирующим натриевые каналы, в опытах с фиксацией мембранного потенциала пропадает первая фаза, а тетраэтиламмоний прекращающий перенос через мембрану калия, вызывает исчезновение второй фазы.

Таким образом, установлено, что формирование потенциала действия вызывается ионными потоками через мембрану: сначала ионов натрия внутрь клетки, а затем - ионов калия из клетки в наружный раствор, что связано с изменением проводимости мембраны для ионов калия и натрия.

Распространение нервного импульса вдоль возбудимого волокна

Если в каком-нибудь участке возбудимой мембраны сформировался потенциал действия, мембрана деполяризована, возбуждение распространяется на другие участки мембраны. Рассмотрим распространение возбуждения на примере передачи нервного импульса по аксону (рис.).

Рис. 19. Локальные токи при распространении нервного импульса по нервному волокну

И в аксоплазме, и в окружающем растворе возникают локальные токи: между участками поверхности мембраны с большим потенциалом (положительно заряженными) и участками с меньшим потенциалом (отрицательно заряженными).

Локальные токи образуются и внутри аксона, и на наружной его поверхности. Локальные электрические токи приводят к повышению потенциала внутренней поверхности невозбужденного участка мембраны φ_вн и к понижению φ_нар наружного потенциала невозбужденного участка мембраны, оказавшегося по соседству с возбужденной зоной. Таким образом, отрицательный потенциал покоя φ^п уменьшается по абсолютной величине, то есть повышается. В областях, близких к возбужденному участку,φ_м повышается выше порогового значения. Под действием изменения мембранного потенциала открываются натриевые каналы и дальнейшее повышение происходит уже за счет потока ионов натрия через мембрану.

Происходит деполяризация мембраны, развивается потенциал действия. Затем возбуждение передается дальше на покоящиеся участки мембраны.

Может возникнуть вопрос, почему возбуждение распространяется по аксону не в обе стороны от зоны, до которой дошло возбуждение, ведь локальные токи текут в обе стороны от возбужденного участка. Дело в том, что возбуждение может распространяться только в область мембраны, находящуюся в состоянии покоя, то есть в одну сторону от возбужденного участка аксона. В другую сторону нервный импульс не может распространяться, так как области, через которые прошло возбуждение, некоторое время остаются невозбудимыми - рефрактерными.

Повышение мембранного потенциала - величина деполяризующего потенциала V, передаваемого от возбужденных участков вдоль мембраны, зависит от расстояния х (как это следует из электродинамики) по формуле:

V₀ - повышение мембранного потенциала в зоне возбуждения, х - расстояние от возбужденного участка; λ, - константа длины нервного волокна, равная расстоянию, на котором деполяризующий потенциал уменьшается в е раз...

Константа длины нервного волокна

,

где r_m - удельное электрическое сопротивление оболочки волокна. δ - толщина оболочки, а - радиус нервного волокна, r_i. - удельное электрическое сопротивление цитоплазмы. Чем больше константа длины мембраны, тем больше скорость распространения нервного импульса. Величина λ тем больше, чем больше радиус аксона и удельное сопротивление мембраны и чем меньше удельное сопротивление цитоплазмы.

Большую скорость распространения нервного импульса по аксону кальмара обеспечивает их гигантский по сравнению с аксонами позвоночных диаметр. У позвоночных большая скорость передачи возбуждения в нервных волокнах достигается другими способами. Аксоны позвоночных снабжены ми-елиновой оболочкой, которая увеличивает сопротивление мембраны и ее толщину.

Рис.20. Сальтаторное распространение потенциала действия по миелинизированному волокну

Возбуждение по миелинизированному волокну распространяется сальтаторно (скачкообразно) от одного перехвата Ранвье (участка, свободного от миелиновой оболочки) до другого. Нервные импульсы проводятся по аксонам в какой-то степени аналогично тому, как передаются электрические сигналы по кабельно-релейной линии. Электрический импульс передается без затухания за счет его усиления на промежуточных релейных станциях, роль которых в аксонах выполняют участки возбудимой мембраны, в которых генерируются потенциалы действия.