 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Частотные характеристики звена
|
|
Частотными характеристиками (ч.х.) называются формулы и графики, характеризующие реакцию звена на синусоидальное входное воздействие в установившемся режиме, т.е. вынужденные синусоидальные колебания звена.
Если на вход звена подается 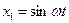 , то на выходе будет:
, то на выходе будет: 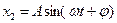 , где
, где 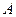 – амплитуда (точнее, усиление амплитуды колебаний, а
– амплитуда (точнее, усиление амплитуды колебаний, а 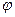 – фаза (точнее, сдвиг по фазе).
– фаза (точнее, сдвиг по фазе).
Применяется символическая запись синусоидальных колебаний в виде: 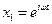
Допустим, уравнение звена имеет вид: 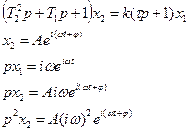
Если применить символьную запись переменных, то ДУ звена будет иметь вид:
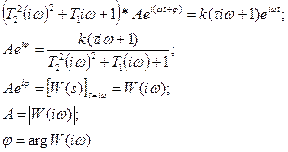
В общем виде: 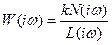 (*)
(*)
Т.о., получить АФЧХ можно из передаточной функции, подставив оператор 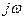 вместо
вместо 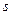 . Иногда АФЧХ называется частотной передаточной функцией звена. Выражения (*) называются соответственно амплитудной частотной характеристикой и фазовой частотной характеристикой звена.
. Иногда АФЧХ называется частотной передаточной функцией звена. Выражения (*) называются соответственно амплитудной частотной характеристикой и фазовой частотной характеристикой звена.
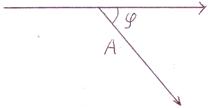
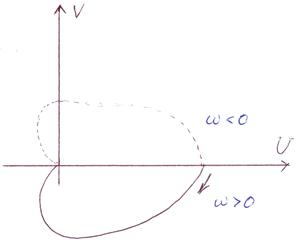
Графически АФЧХ изображается на плоскости в полярных координатах. Но можно также изображать её и в прямоугольных координатах 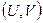
| 
|
 где
где 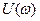 - действительная часть, а
- действительная часть, а 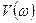 - мнимая часть АФЧХ
- мнимая часть АФЧХ
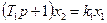 ;
; 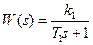
Пример:
1)
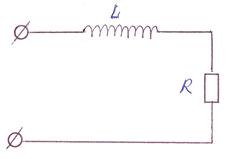
2)электродвигатель в 1-м приближении:  - упр.
- упр. 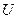 ,
, 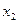 - угловая скорость вала.
- угловая скорость вала.
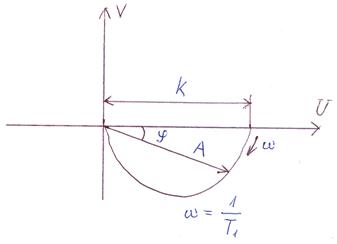
АФЧХ апериодического звена.
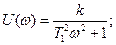 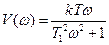 . .
| 
|
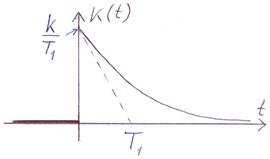
| Переходная функция: | Весовая функция: |
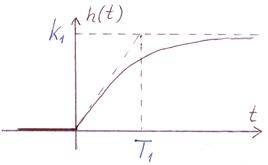
| 
|
АФЧХ апериодического звена 2-го порядка:
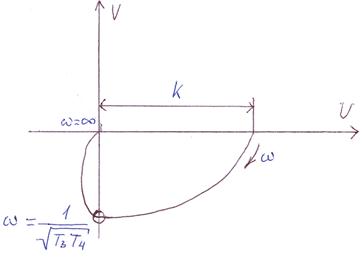
| Переходная функция: | Весовая функция: |
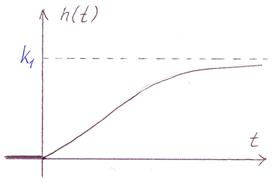
| 
|
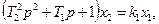
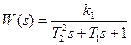 , где
, где 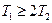
ПФ апериодического звена 2-го порядка можно записать так:
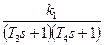 , где
, где 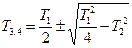
АФЧХ: 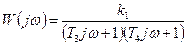
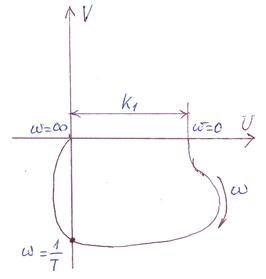
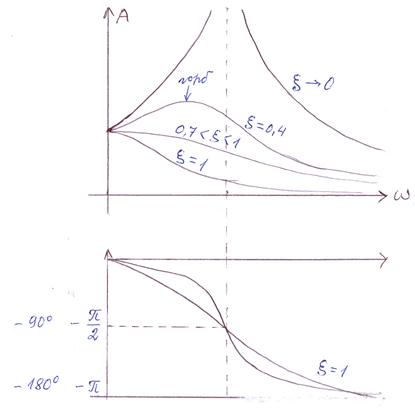
АФЧХ колебательного звена: 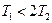
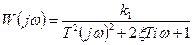
| 
|
Амплитудная характеристика при разных 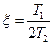
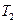 - раскачивает колебания, - раскачивает колебания,
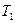 - демпфирует - демпфирует
| 
|
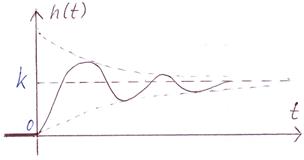
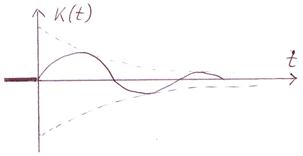
| Переходная функция колебательного звена: | Весовая функция колебательного звена: |
| 
|
При 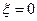 , когда
, когда 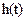 и
и 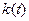 становятся незатухающими (периодическими), колебательное звено становится консервативным.
становятся незатухающими (периодическими), колебательное звено становится консервативным.
Интегрирующие звенья.
Передаточные функции интегрирующих звеньев имеют вид:
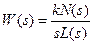 или
или 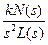 ,
,
где L(s) имеет свободный член, равный 1, как и 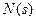 .
.
У дифференцирующих звеньев в числителе передаточной функции отсутствует свободный член, т.е. для однократно дифференцирующего звена ПФ имеет вид:
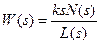
Для двукратно дифференцирующего звена:
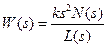
Идеальное интегрирующее звено.
 или
или 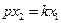
Передаточная функция:
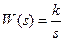
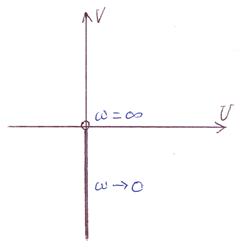
АФЧХ звена:
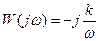 ; ; 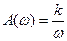 ; ; 
| 
|
| Переходная функция: | 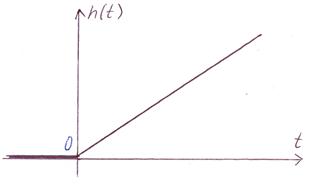
|
| Весовая функция: | 
|
Пимеры идеального интегрирующего звена: гидравлический демпфер, операционный усилитель в режиме интегрирования (????)
Интегрирующее звено с запаздыванием.
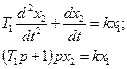

Интегрирующее звено с запаздыванием можно представить как совокупность двух включенных последовательно звеньев: идеального интегрирующего и апериодического первого порядка.
АФЧХ: 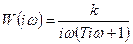
| 
|
| Переходная функция: | 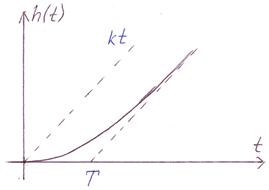
|
| Весовая функция: | 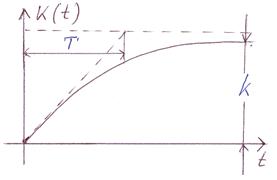
|
Примером инерционного интегрирующего звена можно считать электродвигатель, если выходной величиной считать угол поворота вала двигателя.
Идеальное дифференцирующее звено.
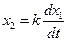 ;
; 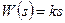
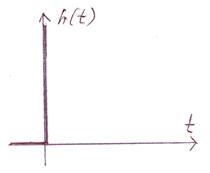
Переходная функция: 
| 
|
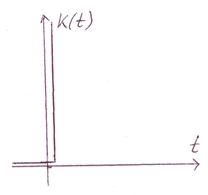
Весовая функция: 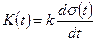
| 
|
Пример ИДЗ – тахогенератор постоянного тока.
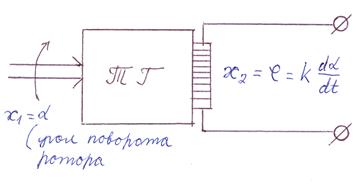
При этом входная величина – угол поворота ротора, а выходная – ЭДС якоря
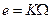 , где
, где 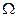 - скорость вращения ротора,
- скорость вращения ротора, 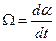
Следовательно, 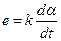 . В режиме, близком к холостому ходу (сопротивление нагрузки генератора велико), можно считать, что напряжение якоря равно ЭДС
. В режиме, близком к холостому ходу (сопротивление нагрузки генератора велико), можно считать, что напряжение якоря равно ЭДС  . Тогда
. Тогда
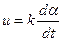
АФЧХ: 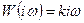
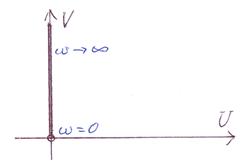
| 
|
Дифференцирующее звено с запаздыванием.
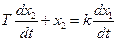
ПФ звена:
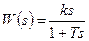
Звено условно можно представить в виде последовательно включенных звеньев – идеального дифференцирующего и апериодического 1-го порядка.
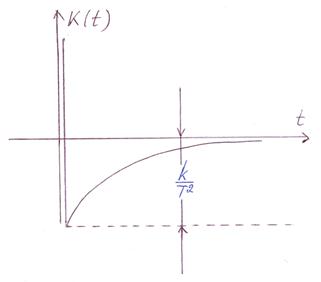
| Переходная функция: | Весовая функция: |
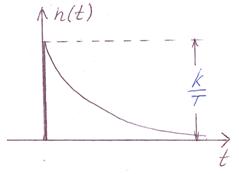
| 
|
АФЧХ: 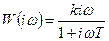
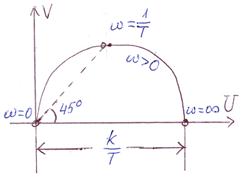
| 
|
Примеры: обычная цепочка 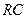 , трансформатор, механический демпфер с пружиной,
, трансформатор, механический демпфер с пружиной, 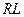 - цепочка.
- цепочка.
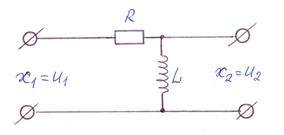
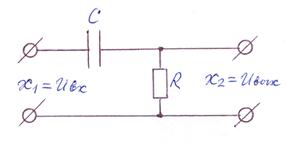
Составим уравнение, например, для 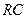 цепочки (дифференцир. конденсатора).
цепочки (дифференцир. конденсатора).
| 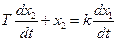
|
Ток в рассматриваемой цепи определяется уравнением:

Перейдем к изображениям и решим уравнение относительно тока:
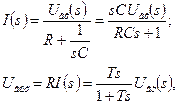 где
где 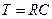 - постоянная времени цепи.
- постоянная времени цепи.
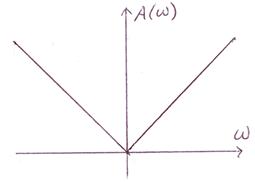
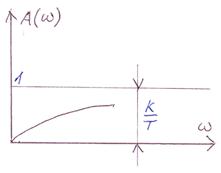
Амплитудно - частотная характеристика идеального дифференцирующего звена имеет вид линейной функции. Характеристика же реального дифференцирующего звена в области высоких частот отличается от нее. 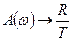 .
.
При 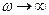 сигнал стремится к значению
сигнал стремится к значению  . Для звеньев, представляющих собой
. Для звеньев, представляющих собой 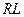 и
и 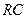 -цепи,
-цепи, 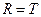 и на высоких частотах
и на высоких частотах 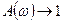 .
.
Дата публикования: 2014-11-04; Прочитано: 1117 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
