Дж.К.Максвелл

Основные вопросы. Требование универсальности. Система пространственно-временных величин. Система LT как универсальный словарь базовых понятий прикладных математических теорий. Меры Пространства. Меры Времени. Стандартное изображение законов природы. Тензорное выражение закона природы. Обобщенные свойства систем LT. Иерархия величин. Энергия и мощность. Свободная и связная энергия. Температура и энтропия. Связь свободной энергии с потенциальной и кинетической. Поток свободной энергии и обобщенная машина. Классы систем реального мира. Замкнутые и открытые системы. (Определение замкнутой системы. Определение открытой системы.) Полная мощность. Полезная мощность и мощность потерь. Уравнение полной мощности. Связь мощности, энергии и энтропии. Различные формы энергии и мощности. Закон сохранения мощности. Равновесные и неравновесные системы. Диссипативные и антидиссипативные процессы. Устойчивость. Неустойчивое равновесие. Механизм устойчивой неравновесности. Механизм развития. Устойчивое развитие. Перспективы развития идей.

1. Основные вопросы

Физику можно разделить на экспериментальную и теоретическую. Экспериментальную физику прежде всего интересует: «Что измерять?» и «Как измерять?» Ключевой вопрос теоретической физики: «Какую физическую величину принять в качестве инварианта при исследовании тех или иных явлений материального мира?» Отсюда следует, что связующим звеном между экспериментальной и теоретической физикой выступает «Физическая величина». Она выполняет функцию ЭТАЛОНА.

2. Требование универсальности

Однако далеко не каждая величина может быть УНИВЕРСАЛЬНЫМ ЭТАЛОНОМ.

В соответствии с требованиями Дж.Максвелла, А.Пуанкаре, Н.Бора, А.Эйнштейна, В.И.Вернадского, Р.Бартини физическая величина является универсальной тогда и только тогда, когда ясна ее связь с пространством и временем. И тем не менее, до трактата Дж.К.Максвелла «Об электричестве и магнетизме» (1873) не была установлена связь размерности массы с длиной и временем, что и является причиной использования в качестве основных единиц не только длины и времени, но и массы.

Поскольку введение размерности для МАССЫ — [ L ³ T ^-2] — введено Максвеллом, вместе с обозначением в виде квадратных скобок, то позволим себе привести отрывок из работы самого Максвелла:

Дж.К.Максвелл. «Трактат об электричестве и магнетизме» (М.: Наука, 1989):

«ОБ ИЗМЕРЕНИИ ВЕЛИЧИН

1. Любое выражение для какой-нибудь Величины состоит из двух факторов или компонент. Одним из таковых является наименование некоторой известной величины того же типа, что и величина, которую мы выражаем. Она берется в качестве эталона отсчета. Другим компонентом служит число, показывающее, сколько раз надо приложить эталон для получения требуемой величины. Эталонная стандартная величина называется в технике Единицей, а соответствующее число — Числовым Значением данной величины.

2. При построении математической системы мы считаем основные единицы — длины, времени и массы — заданными, а все производные единицы выводим из них с помощью простейших приемлемых определений.

Следовательно, во всех научных исследованиях очень важно использовать единицы, принадлежащие системе, должным образом определенной, равно как и знать их связи с основными единицами, чтобы иметь возможность сразу же пересчитывать результаты одной системы в другую.

Знание размерности единиц снабжает нас способом проверки, который следует применять к уравнениям, полученным в результате длительных исследований.

Размерность каждого из членов уравнения относительно каждой из трех основных единиц должна быть одной и той же. Если это не так, то уравнение бессмысленно, оно содержит какую-то ошибку, поскольку его интерпретация оказывается разной и зависящей от той произвольной системы единиц, которую мы принимаем.

ТРИ ОСНОВНЫЕ ЕДИНИЦЫ

3. (1) ДЛИНА. Эталоном длины, используемым в нашей стране в научных целях, служит фут, который составляет третью часть стандартного ярда, хранящегося в Казначейской Палате.

Во Франции и других странах, принявших метрическую систему, эталоном длины является метр. Теоретически это одна десятимиллионная часть длины земного меридиана, измеренного от полюса до экватора; практически же это длина хранящегося в Париже эталона, изготовленного Борда (Borda) с таким расчетом, чтобы при температуре таянья льда он соответствовал значению длины меридиана, полученному Даламбером. Измерения, отражающие новые и более точные измерения Земли, не вносятся в метр, наоборот, — сама дуга меридиана исчисляется в первоначальных метрах.

В астрономии за единицу длины принимается иногда среднее расстояние от Земли до Солнца.

При современном состоянии науки наиболее универсальным эталоном длины из числа тех, которые можно было бы предложить, служила бы длина волны света определенного вида, испускаемого каким-либо широко распространенным веществом (например, натрием), имеющим в своем спектре четко отождествляемые линии. Такой эталон не зависел бы от каких-либо изменений в размерах Земли, и его следовало бы принять тем, кто надеется, что их писания окажутся более долговечными, чем это небесное тело.

При работе с размерностями единиц мы будем обозначать единицу длины как [ L ]. Если численное значение длины равно l, то это понимается как значение, выраженное через определенную единицу [ L ], так что вся истинная длина представляется как l [ L ].

4. (2) ВРЕМЯ. Во всех цивилизованных странах стандартная единица времени выводится из периода обращения Земли вокруг своей оси. Звездные сутки или истинный период обращения Земли может быть установлен с большой точностью при обычных астрономических наблюдениях, а средние солнечные сутки могут быть вычислены из звездных суток благодаря нашему знанию продолжительности года.

Секунда среднего солнечного времени принята в качестве единицы времени во всех физических исследованиях.

В астрономии за единицу времени иногда берется год. Более универсальную единицу времени можно было бы установить, взяв период колебаний того самого света, длина волны которого равна единице длины.

Мы будем именовать конкретную единицу времени как [ T ], а числовую меру времени обозначать через t.

5. (3) МАССА. В нашей стране стандартной единицей массы является эталонный коммерческий фунт (avoirdupois pound), хранящийся в Казначейской Палате. Часто используемый в качестве единицы гран (grain) составляет одну 7000-ю долю этого фунта.

В метрической системе единицей массы служит грамм; теоретически это масса кубического сантиметра дистиллированной воды при стандартных значениях температуры и давления, а практически это одна тысячная часть эталонного килограмма, хранящегося в Париже*.

Но если, как это делается во французской системе, определенное вещество, а именно вода, берется в качестве эталона плотности, то единица массы уже перестает быть независимой, а изменяется подобно единице объема, т.е. как [ L ³]. Если же, как в астрономической системе, единица массы выражена через силу ее притяжения, то размерность [ M ] оказывается такой [ L ³ T ^-2]».

Максвелл показывает, что массу можно исключить из числа основных размерных величин. Это достигается с помощью двух определений понятия «сила»:

1) 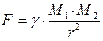и 2) .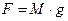

Приравнивая эти два выражения и считая гравитационную постоянную безразмерной величиной, Максвелл получает:

, [ M ] = [ L ³ T ^-2].

Масса оказалась пространственно-временной величиной. Ее размерность: объем 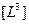с угловым ускорением 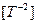(или плотностью, имеющей ту же размерность ).

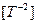Величина массы стала удовлетворять требованию универсальности. Появилась возможность выразить все другие физические величины в пространственно-временных единицах измерения.

Так выглядел результат в 1873 г., а еще раньше в 1716 г. к такой возможности пришел Герман, в так называемой Форономии.

3. Система пространственно-временных величин

В 1965 г. в Докладах АН СССР №4 была опубликована статья Р.Бартини «Кинематическая система физических величин». Эти результаты — малоизвестные, но имеют исключительно важное значение для обсуждаемой проблемы. В 1973 г. Р.Бартини показывал нам пожелтевший от времени лист бумаги с таблицей, написанной им в 1936—1937 гг. В этой таблице он установил пространственно-временную размерность любой физической величины и использовал ее для проверки аналитических выкладок. К аналогичному результату, но в 1967 г., пришел академик Е.Седов, а в 1969 г. — академики Л.Ландау и Е.Лифшиц.

В системе пространственно-временных величин размерность любой физической величины выражается ЦЕЛЫМИ (положительными или отрицательными) ЧИСЛАМИ. Здесь нет дробных степеней, которые лишают сам анализ размерности его прикладного значения (рис. 3.1).

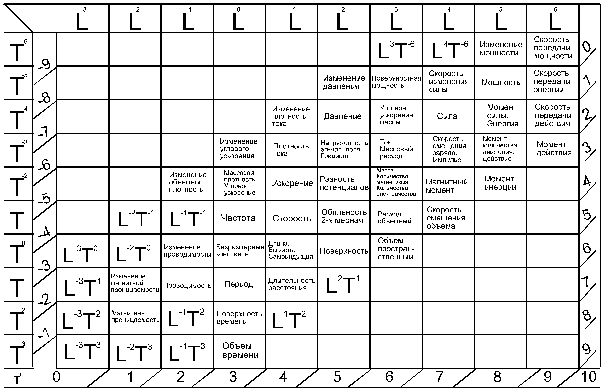
Рис. 3.1. Система пространственно-временных величин

4. Система LT как универсальный словарь базовых понятий прикладных математических теорий

Система оказалась универсальным словарем понятий для всех прикладных математических теорий. Это тот словарь, отсутствие которого заводит в тупик при попытке сконструировать формальную математическую теорию без использования физически измеримых величин. Хотя система универсальных величин весьма «проста» — это только «видимость». В настоящее время в работах физиков теоретиков по общей теории относительности используются еще «более простые» системы, построенные на одной размерной величине. Так, например, Дж.Уилер использует одну величину — длину [ L ], а Дж.Синг — только время [ T ]. Однако там возникают проблемы дробных степеней. По отношению к этим конструкциям система из двух единиц — длины [ L ] и времени [ T ] — может считаться не очень «экономной». Однако, хотя основных величин в системе только две, они имеют векторный характер, т.е. каждая из них имеет три орты.

Они обозначаются: 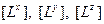— для ориентированных длин и 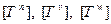— для ориентированных времен.

«Элементарный (3 + 3)-мерный образ можно рассматривать как волну и как вращающийся осциллятор, попеременно являющийся стоком и источником, образованным сингулярностью преобразований. В осцилляторе происходит поляризация компонентов фона, преобразование L ® T или T ® L в зависимости от ориентации осциллятора, создающего ветвление L - и Т -протяженностей. Элементарный осциллятор является зарядом, создающим вокруг себя и внутри себя поле» (Р.Бартини).

На такую же возможность (3 + 3)-мерного представления L и Т обращал внимание еще Ханкеле.

Если отбросить на время фиксированные индексы ориентации, то любая физическая величина представляется «брутто-формулой»:

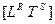, (3.1)

где R и S — ЦЕЛЫЕ (положительные и отрицательные) ЧИСЛА.

Все физически измеряемые величины выводятся из двух основных и представляются в виде произведения целочисленных степеней длины 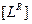и времени . При различных R и S имеем: безразмерные константы 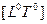, объекты геометрии , «временные» (в частности, частотно-временные) . Соединение «пространственных» и «временных» величин дает словарь универсальных понятий.

5. Меры Пространства

Если положить S = 0, то формула примет вид = = .

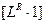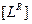То есть после исключения понятия ВРЕМЯ, мы приходим к системе величин А.Лебега. Действительно: 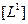= длина; = площадь; 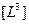= объем; 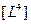= тор; 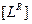= гипертор R -го порядка.

Считая размерную величину 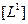= длина — константой, как принято выражаться у Н.Бурбаки, явной аксиомой, мы получим понятие абсолютно твердое тело, имеющее колоссальное значение для «обоснования математики». При переходе в другую область, например, в гидродинамику, нам придется заменить явную аксиому

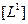= const

на другую явную аксиому:

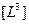= const.

В новой «системе тел» по А.Лебегу «расстояние» между точками по-прежнему будет числом, но не будет «величиной» относительно «объема».

Но, если мы изучаем вращение свободных тел, то нам нужно рассмотреть произведение радиуса вращения на угловую скорость. Как известно, это произведение есть функция постоянная для всех тел, независимо от их размеров. Имеем:

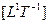= const.

Здесь появляется время.

Если положить R = 0, то формула (1) принимает вид:

= ,

то есть после исключения понятия длина, мы получаем систему понятий, описывающих ВРЕМЯ.

6. Меры Времени

При S > 0 имеем пространственные меры времени: 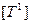— период; 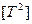— поверхность времени; — объем времени.

При S < 0 — частотные меры времени: 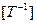— частота; 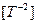— угловое ускорение; — гиперчастота S -порядка.

Измерение времени существенно отлично от измерения «длины», так как не существует «абсолютно твердого тела», которое могло бы служить «мерой» интервала. Это второе положение должно выразить «Нетелесную сущность» понятия «время». Известна мысль Аристотеля: «время — число движения».

Но здесь нужно вспомнить о работе Дж.Б.Брауна, опубликованной в 1941 году. Он тщательно рассмотрел процедуру измерения времени.

Все знают, что время нельзя измерять «линейкой». Браун обратил внимание на измерение астрономического времени, которое состоит в получении «отсчетов» при совпадении определенной «неподвижной звезды» с перекрестием телескопа. Эти отсчеты названы «моментами». Наблюдатель называет эти «моменты» порядковыми числами и становится любимой фигурой тех математиков, которым желательно иметь «конструктивное определение натурального ряда». Однако этот наблюдатель ничего не может сказать о «расстоянии» между моментами, так как это требует гипотезы «равенства интервалов». Но математики очень красиво обошли эту физическую трудность. Было предложено «измерять интервал» между «моментами» с помощью угловой меры. Действительно, мы имеем плоское циклическое движение: звезда регулярно совпадает с перекрестием, а между двумя «моментами» находится под углом от 0 до 2 относительно оси телескопа.

Вывод из анализа процедуры измерения времени может быть такой:

Измерение времени использует циклический процесс, что сообщает характеру движения два свойства:

· · Дискретность отсчетов;

· · Замкнутость траектории.

Таким образом введены два класса понятий:

1) пространственные понятия ;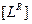

2) временные понятия .

Их соединение даст полную систему универсальных понятий .

7. Стандартное изображение законов природы

Оживим наши понятия. Если предыдущие рассуждения справедливы, то приравнивание величин = const может быть стандартным изображением законов природы.

(1609 г.) Закон Кеплера: «Радиус-вектор планеты за равные промежутки времени заметает равные площади»

(1619 г.) Закон Кеплера: «Отношение куба радиуса планеты к квадрату периода обращения есть величина постоянная»

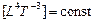(1686 г.) Закон сохранения количества движения, или Закон сохранения импульса (Ньютон)

(1686 г.) Закон всемирного тяготения (Ньютон)

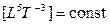(1800 г.) Закон сохранения момента количества движения (Лаплас)

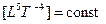(1842 г.) Закон сохранения энергии (Р.Майер)

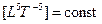(1789, 1855 гг.) Закон сохранения мощности (Лагранж, 1789; Максвелл, 1855).

Мы видим, что наряду с хорошо известными законами: сохранения импульса, момента количества движения и энергии, обнаруживается и малоизвестный закон сохранения мощности.

8. Тензорное выражение закона природы

Согласно принципу инвариантности «общие законы природы должны быть выражены через уравнения, справедливые во всех допустимых координатных системах, то есть эти уравнения должны быть ковариантными относительно любых подстановок» (А.Эйнштейн).

Сущностью закона природы может считаться эмпирически подтвержденное обобщение — утверждение о том, «что некоторая величина остается инвариантом, независящим от выбранной системы координат (независящим от точки зрения наблюдателя) в определенном классе систем» = const.

Рассмотрим запись закона в координатах. С этой целью будем связывать величины таблицы Ди-Бартини с соответствующими тензорами. Сделаем оговорку относительно правила написания индексов. Степень длины (положительная) дает число контрвариантных индексов, которые будем писать справа вверху, а отрицательная степень времени дает число ковариантных индексов справа снизу. Для обратных величин индексы пишутся слева и меняются местами: отрицательные степени длины — ковариантны, а положительные степени времени — контрвариантны. При таком расположении индексов любая величина таблицы может быть легко опознана. Покажем это на примере кинематики точки. Уравнение в координатах принимает вид:

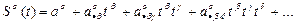
где 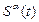— длина пути, пройденного точкой; — смещение; 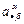— скорость; 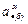— ускорение; 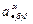— изменение ускорения; и т.д. 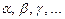= 1, 2, 3.

Следует заметить, что в приведенной записи ВРЕМЯ имеет три измерения, то есть мы работаем в (3 + 3)-мире Бартини, а не в (3 + 1)-мире Эйнштейна. Это различие масштабов времени по различным направлениям здесь закладывается с самого начала, что приводит к ясному пониманию неравенства «поперечного» и «продольного» времени, которое доставило массу неприятностей физикам начала XX века.

Запишем теперь известные законы в тензорной форме:

закон Кеплера: К = ( 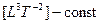) = 0, или = 0;

закон Ньютона: Н = ( ) = 0, или = 0;

закон Лапласа: Л = ( 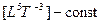) = 0, или 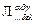= 0;

закон Майера: М = ( 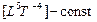) = 0, или = 0;

закон Максвелла: m = ( 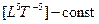) = 0, или .

Подведем предварительные итоги.

9. Обобщенные свойства систем LT

Каждая величина — это, прежде всего, понятие, отражающее сущность — инвариант определенного класса систем реального мира, включая микро-, макро- и супермир. Каждая величина — это:

· · качественно-количественная определенность, где качество определяется именем, размерностью и единицей измерения, а количество — численными значениями величины;

· · тензор, как группа преобразований с инвариантом. Он может быть представлен как скаляр, вектор, полиэдральный вектор;

· · поток-волна, имеющий определенную размерность длины и частоты.

Переход от одной величины-понятия к другой означает переход к другой системе-механизму: с другой сущностью — инвариантом, другим качеством, другой группой преобразования, с другими волновыми потоками.

Система в целом — это, прежде всего, полная система универсальных понятий отображающих сущность систем реального мира.

Она является бесконечной. Это означает, что не существует ограничений на количество величин-понятий. В ходе развития научной мысли их список будет все время пополняться.

10. Иерархия величин

Система представляет иерархию вложенных понятий. Величина, являющаяся сущностью одного класса систем, может быть явлением-проекцией другого нижележащего класса систем. На данное время в вершине этой иерархии находятся понятия: мощность и мобильность (скорость переноса мощности). Другие величины имеют меньшую пространственно-временную размерность и поэтому могут быть выведены. Покажем это на примере величин, у которых размерность длины и времени одинаковые, но с разным знаком. Эти величины пересекают всю таблицу (см. рис. 3.1) по диагонали, разделяя ее на две части и образуя группу симметрично-инверсных, или «осевых», величин:

— константа;

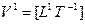— скорость;

— разность потенциалов;

— ток;

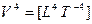— сила;

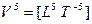— мощность.

Все представленные величины различаются по скоростям и являются вложенными одна в другую, образуя полиэдральный куб (рис. 3.2).

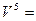мощность

сила

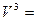ток

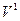
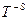
Рис. 3.2

Здесь наглядно видно, что величиной, объединяющей всю группу, является мощность. Все другие симметрично-инверсные величины являются составными элементами мощности и могут быть через нее выражены. В этом смысле мощность является наиболее общей величиной. Закон сохранения мощности имеет наибольшую силу, охватывая наиболее широкий класс систем. В классических консервативных системах требуется постоянство скорости. Это требование снимается при работе с инвариантом мощности.

В дальнейшем изложении это утверждение будет предметом специального рассмотрения.

11. Энергия и мощность

В системе энергия имеет размерность , а мощность — .

Основным свойством энергии является ее способность совершать работу в процессе превращения из одной формы в другую.

Основным свойством мощности является работоспособность в единицу времени.

По этой причине полная энергия Е произвольной системы является суммой двух частей:

1) 1) превратимой, или свободной, энергии В,

2) 2) непревратимой, или связной, энергии А (при данных природных и технологических условиях)

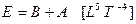. (3.2)

12. Свободная и связная энергия

Если полное максимальное значение энергии системы обозначить E _max, а минимальное значение энергии — E _min, тогда мы получаем еще одно значение энергии, которое есть разность между максимальным и минимальным значением энергии — это «свободная энергия» В:

В = E _своб= E _max- E _min. (3.3)

Мы можем записать

E _max = E _своб + E _min. (3.4)

Минимальное значение энергии E _min называется «связной энергией» А. Обозначая «связную энергию» º «минимальной энергии» А = E _связ, получим

E _max = E _своб + E _связ , или E _max = В + А. (3.5)

Очевидно, что E _max в классической термодинамике называется полной энергией системы.

«Одномерное» пространство можно изображать в виде «отрезка», состоящего из двух компонент: «свободной» энергии и «связной» энергии. Изобразим это на рис. 3.3.

1 А 2 В 3

	E связ			E своб
«связная» энергия	«свободная» энергия E полн
полная энергия

Рис. 3.3. Одномерное фазовое пространство энергии

Очевидно, что на этой диаграмме любое состояние системы представляется точкой 2, которая лежит МЕЖДУ точкой 1 и точкой 3.

В зависимости от значения «свободной» и «связной» энергии состояние системы изменяется, что проявляется в перемещении «точки 2». При увеличении «свободной» энергии точка перемещается влево, а при увеличении «связной» энергии — вправо.

Состояние системы может быть определено по соотношению «свободной» и «связной» энергий. Понятно, что чем больше значение «свободной» энергии, тем выше работоспособность системы. Поэтому отношение «свободной» энергии к полной энергии определяет коэффициент полезного действия (КПД) системы:

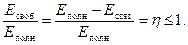(3.6)

Очевидно, что КПД системы достигает значения 1, когда «связная» энергия обращается в нуль, и, наоборот, — КПД системы достигает значения близкого к нулю, когда связная энергия приближается к значению полной энергии системы.

Поэтому очень важно правильно определить «полную», «свободную» и «связную» энергии системы.

Естественно в этой связи обратиться к термодинамике, где и было введено понятие термодинамического коэффициента полезного действия для паровых машин, когда появился цикл Карно. Впоследствии в уравнениях Гельмгольца и Гиббса была показана связь «полной», «свободной» и «связной» энергий для изотермически замкнутых систем. В уравнениях Гельмгольца эта связь выглядит следующим образом:

E _полн = E _своб + T × S. (3.7)

Здесь «связная» энергия представляется произведением температуры Т термометрического тела и энтропии S изолированной системы.

Однако, нетрудно убедиться в том, что понятия «температура» и «энтропия» в пространственно-временной системе отсутствуют. Это обстоятельство вынуждает нас рассмотреть эти понятия внимательней.

13. Температура и энтропия

Для определения связной энергии нужно измерять энтропию и температуру. Но что это такое?

Мы хотели бы обратить внимание на одну «физическую константу», известную как константа Больцмана. Константа Больцмана k = 1,38054 ´ 10^-16 эрг×град^-1 фигурирует в физике, как «постоянная» и связывает классическую термодинамику со статистической физикой, как в классическом случае, так и в квантовой механике. Действительно ли это «физическая постоянная»? Нетрудно доказать, что это не так.

Известно, что в школьной физике, да и в учебниках высшей школы, фигурирует формула:

E = pV = RT. (3.8)

Здесь E — энергия, накопленная в форме тепла в газе, p — давление газа, V — объем газа, R — газовая постоянная, T — температура газа.

Вообще говоря, такую зависимость теоретическая физика имеет только для «идеального газа».

Через некоторое время, когда было обнаружено, что теплоемкость газов различна и зависит от числа степеней свободы (которые считались определяемыми числом атомов в молекуле), было принято соглашение относить постоянную R не к одному молю газа, а относить на одну «степень свободы» молекулы — это соглашение превратило «газовую постоянную» в «константу Больцмана». Эта последняя выражается отношением газовой постоянной к числу молекул в грамм-молекуле.

k = R: N = 1,38054 ´ 10^-16 эрг×град^-1. (3.9)

Некоторое время спустя эту константу начали умножать на множитель, зависящий от сложности молекул, используя представление о степенях свободы. Формула (3.8) приобретает вид:

E = pV = nkNT, (3.10)

где E — энергия газа, p — давление газа, V — объем газа, kN = R — газовая постоянная, n — множитель, учитывающий число степеней свободы и принимающий значения: 3/2, 5/2, 7/2, … Через некоторое время спустя снова пришлось корректировать формулу теплоемкости газа, которая оказалась сама зависящей от температуры. Традиционный математический прием аппроксимации изменяющейся величины — это разложение в ряд по степеням независимой переменной. Возвращаясь снова к газовой постоянной (разложение в степенной ряд лишает эту величину статуса постоянной — теперь она переменная, представляемая суммой ряда) запишем разложение в ряд по степеням температуры:

E = pV = (R ₀+ R ₁ T + R ₂ T ²+ R ₃ T ³+ …) T. (3.11)

Мы получили новый вид функции, выражающий ИЗМЕНЕНИЕ теплоемкости газа в зависимости от температуры, то есть установили, что газовая «постоянная» НЕ ЯВЛЯЕТСЯ «ПОСТОЯННОЙ», а что эта величина изменяется с изменением температуры. Формула (3.11) имеет очень громоздкий вид. Для уменьшения числа членов в степенном ряду можно заменить этот ряд некоторой новой буквой, заменяющей этот ряд. Выбираем для этого обозначения букву S. Имеем:

S = R ₀+ R ₁ T + R ₂ T ²+ R ₃ T ³+ … (3.12)

Подставляем это значение в формулу (3.11), но не будем забывать, что скрывается за символом S:

E = pV = ST. (3.13)

Сравним формулу (3.13) с формулой (3.8) и зададимся вопросом: «На какой же формуле базируется статистическая физика?»

Ведь нельзя ПОСТУЛИРОВАТЬ в рамках одной и той же теории в качестве ИСТИННЫХ — ДВЕ различные формулы для одной и той же энергии газа.

Физик сразу же поймет, что буква S выбрана не случайно — да, это и есть ЭНТРОПИЯ. Нетрудно убедиться в этом, записывая выражение для «свободной энергии»:

F = pV - ST. (3.14)

Дифференцируя это выражение, мы получим хорошо известную формулу изменения свободной энергии:

dF = p dV + V dp - S dT - T dS. (3.15)

Интеграл от этого полного дифференциала возвращает нас к формулам (3.14) и (3.13). Для начала заметим, что для равновесных систем свободная энергия равна нулю. С другой стороны, обращаясь к формуле (3.11) и к формуле (3.13), зададимся не традиционным вопросом: «Что такое ЭНТРОПИЯ?», а вопросом: «Что мы измеряем, когда измеряем температуру?» Ведь измерение температуры задавалось правилом, что при постоянном давлении между температурой и объемом термометрического тела существует ЛИНЕЙНАЯ ЗАВИСИМОСТЬ, которая и выражается ГАЗОВОЙ ПОСТОЯННОЙ. ЭТО означает, что приращение энергии газа выражается через приращение температуры.

Небольшое размышление показывает, что исторически термин температура связан с изменением объема термометрического тела и ПРЕДПОЛОЖЕНИЕМ О ЛИНЕЙНОЙ ЗАВИСИМОСТИ ЭНЕРГИИ ТЕЛА ОТ ЕГО ОБЪЕМА. В этом случае в формуле (3.8) приращение энергии можно выразить через приращение объема, то есть:

dE = R dV. (3.16)

Здесь мы показываем, что измеряемой физической величиной, которую измеряла классическая физика и называла ТЕМПЕРАТУРОЙ, была величина изменения ОБЪЕМА термометрического тела, что мы делаем и в наши дни при использовании термометров расширения.

Обратимся к формуле (3.13) — здесь та же ситуация, только вместо буквы R стоит буква S. Но физический смысл остается без изменения — эта переменная величина связывает между собою энергию и объем термометрического тела. Имеем:

dE = S dV. (3.17)

При обсуждении парадоксального положения, связанного с использованием в основаниях статистической физики ДВУХ ВЗАИМОИСКЛЮЧАЮЩИХ ФОРМУЛ, приходилось слышать, что величина S существенно ПОЛОЖИТЕЛЬНА. И это положение не выдерживает критики: достаточно заполнить термометр расширения водой и нагревать от 0 до 40° по Цельсию, чтобы получить положительную величину прироста энергии (при уменьшающемся объеме) необходимо считать значение S отрицательным.

Еще в 1961 г. в одной из своих публикаций были показаны абсолютные отрицательные температуры при фазовых переходах, в окислительно-восстановительном потенциале и при фотохимических реакциях.

Вообще, абсолютные отрицательные температуры появляются там, где возможно устойчивое существование микрочастиц на верхнем и нижнем энергетических уровнях — например, фазовый переход и окислительно-восстановительный потенциал (железо-3 — более высокий энергетический уровень, чем железо-2). Фотосинтез: продукты фотосинтеза занимают более высокий энергетический уровень, чем исходные вещества.

Известна работа Э.Шредингера: «Что такое жизнь с точки зрения физики?». В ней Шредингер делает заявление, что растение питается «отрицательной энтропией». Проверка этого утверждения прямым расчетом показала, что Шредингер прав тогда и только тогда, когда температура листа растения имеет абсолютное отрицательное значение. Таким образом, «отрицательная энтропия» имеет ту же природу, что и абсолютные отрицательные температуры.

Вообще говоря, этот вывод хорошо объясняет, почему С.Подолинский, Э.Бауэр, В.Вернадский, а впоследствии и многие другие крупные ученые, для определения физических основ явлений жизни не стали обращаться к понятию ЭНТРОПИЯ, а использовали понятие «свободная энергия».

Мы вновь возвращаемся к этому понятию и хотим показать связь свободной энергии с другими видами энергии.

14. Связь свободной энергии с потенциальной и кинетической

Для установления связи мы будем использовать фазовые диаграммы, которые принято использовать при анализе работы различных машин. Мы можем показать эту связь на примере любого типа машин: механических, термодинамических, электрических, электромагнитных и др. Для простоты изложения воспользуемся обычным маятником (рис. 3.4).

Полная энергия маятника, состоящего из «пружины» и «массы» тела, будет при отсутствии «диссипативных» сил постоянна и состоять из «кинетической» и «потенциальной» энергии и еще какой-то «связной» энергии.

- F + F

Рис. 3.4. Обычный маятник

Наш «маятник» состоит из массы (размещен на тележке, которая катается без трения) и соединен с пружиной, которая обладает жесткостью K. В начальном положении сила натяжения-сжатия пружины равна нулю. Оттянем пружину до некоторой отметки на оси F, т.е. сообщим системе некоторое количество энергии, которое и будет «свободной» энергией. Отпустим тележку — она начнет совершать гармоническое колебание около положения равновесия. Общая и свободная энергия (из-за отсутствия диссипации) будут сохраняться, а «потенциальная» и «кинетическая» энергия будут переходить друг в друга. При этих взаимных переходах представляющая точка D будет перемещаться на отрезке 1—3.

Теперь мы должны «отождествить» наши точки 2 и 3 с точкой D; будем считать, что точка D находится в точке B,когда свободная энергия является «потенциальной» энергией; когда точка D находится в точке 3, то вся свободная энергия является «кинетической». Считая «кинетическую» и «потенциальную» энергию «компонентами» свободной энергии, мы можем рассматривать свободную энергию как векторную сумму своих компонент. Поскольку угол между кинетической и потенциальной энергией — прямой, а свободная энергия — постоянна — инвариант, то представляющая точка D будет описывать окружность (рис. 3.5).

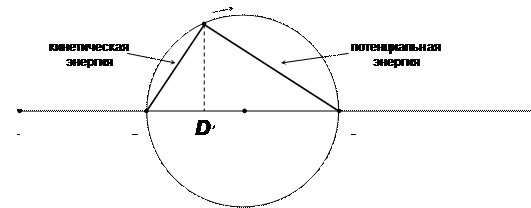
Рис. 3.5. «Гармоническое колебание» обычного маятника

Когда точка D находится в точке 2 — вся свободная энергия находится в форме потенциальной энергии. Когда D проходит через центр окружности, мы имеем равенство кинетической и потенциальной энергии. Приход в точку 3 соответствует пробеганию тележки с максимальной скоростью через нейтральное положение пружины — вся свободная энергия представлена в форме кинетической энергии. При движении по нижней полуокружности точки D происходит сжатие пружины. В точке 2 вся свободная энергия в потенциальной форме сжатия пружины. Следующий оборот точки D возвращает систему в исходное состояние.