Устойчивость движения систем

Система управления постоянно подвергается возмущениям, отклоняющим ее от заданного закона движения. Действие возмущения сопровождается восстанавливающим действием регулятора. В системе возникает переходный процесс. Может оказаться, что система не сможет восстановить требуемый закон движения. Она будет удаляться от него, либо совершать вокруг него незатухающие колебания.

Чтобы определить, устойчиво ли состояние равновесия какой-либо системы, изучается поведение этой системы при малых отклонениях от равновесия.

Под возмущающими факторами понимаются силы, не учитываемые при описании движения вследствие их малости по сравнению с основными силами. Эти возмущающие силы обычно неизвестны: составленные уравнения движения отличаются от истинного движения, в них не учтены некоторые поправочные коэффициенты. Возмущающие силы могут действовать мгновенно, что сведется к малому изменению начального состояния системы (под начальным состоянием системы при выборе оптимального управления понимается начало воздействия возмущений), либо непрерывно. При малых возмущающих воздействиях движение будет устойчивым, при значительных - неустойчивым.

Система обычно находится в состоянии движения, поэтому рассматривают устойчивость движения. Проблема исследования устойчивости движения системы – основная задача теории устойчивости (одна из основных составляющих теории дифференциальных уравнений).

Пусть заданный режим работы системы характеризуется координатами: х ₁₀ (t), х ₂₀ (t), х ₃₀ (t),.... Пусть на систему действует возмущение, которое заставляет двигаться ее по другим траекториям: х ₁ (t), х ₂ (t), х ₃ (t),... Система будет находиться в возмущенном состоянии. Если система устойчива, то она снова войдет в заданный режим или в область около этого режима ε_i = х_i (t) - х_i0 (t).

Заданное невозмущенное состояние движения устойчиво, если в результате возмущений возмущенное состояние движения с течением времени перейдет в некоторую конечную область, находящуюся в окрестности невозмущенного состояния, определяемого координатами:

ε₁ = х₁ (t) – х₁₀ (t);

ε₂ = х₂ (t) – х₂₀ (t);

..........

ε_n = х_n (t) – х_n0 (t).

Признаки устойчивости и неустойчивости движения определяются различными методами теории устойчивости.

Предположим, что система автоматического управления описывается системой дифференциальных уравнений

dу_i /dt = У_i (t, у₁, у₂,..., у_n), (i = 1, 2,..., n). (1)

у_i - переменные параметры, описывающие состояние системы;

У_i – известные функции, определенные в некоторой фиксированной области пространства переменных t, y ₁, y ₂,..., y _n, с начальными условиями у_i (t₀) = у_i0, (i = 1, 2,..., n). Они определяют исходное состояние системы управления при t = t ₀. Каждой системе начальных значений у_i (t₀), (i = 1, 2,..., n) соответствует решение у_i (t₀), (t = 1, 2,..., n) уравнений (1).

Если окажется, что сколь угодно малые изменения начальных состояний способны сильно изменить решение, то решение, определяемое выбранными начальными данными, не имеет практического значения, так как соответствует неустойчивому состоянию системы.

Возникает вопрос о нахождении условий, при которых достаточно малое изменение начальных данных вызывает сколь угодно малое изменение решения, т.е. нахождения условий, при которых система управления, описываемая уравнениями (1) устойчива.

Решение системы (1) называется устойчивым по Ляпунову, если при любой заданной области ε допустимых отклонений от состояния равновесия, можно подобрать область допустимых начальных условий δ = δ (ε), обладающую тем свойством, что ни одно движение, начинающееся внутри δ, никогда не достигнет границ области ε (рисунок 3.5 – двумерный случай).

Таким образом, решение у_i^* (t), (i = 1, 2,..., n) системы (1) устойчиво, если для любого t₀ из интервала [ 0, T ] и числа ε > 0 можно подобрать δ > 0, δ ≡ δ (t ₀, ε) > 0, такое, что всякое решение x_i (t), (i = 1, 2,..., n) той же системы, начальные значения которого удовлетворяют неравенствам

| у_i^* (t₀) - у_i (t₀) | < δ (i = 1, 2,..., n),

определено в промежутке t₀< t < ∞ и для всех t t₀ справедливы неравенства

| у_i^* (t) - у_i (t) | < ε (i = 1, 2,..., n). (2)

Близкие по начальным значениям решения остаются близкими для всех t t_0.

Решение у_i^* (t), (i = 1, 2,..., n) системы (1) называется неустойчивым, если существует область ε допустимых отклонений от состояния равновесия, для которой не существует области δ, окружающей состояние равновесия и обладающей тем свойством, что ни одно движение, начинающееся внутри δ, никогда не достигнет границы области ε, либо если это решение непродолжаемо при t → ∞.

В этом случае при t₀ [0, T ] и сколь угодно малых ε > 0 и δ > 0 хотя бы для одного решения у_i (t), (i = 1, 2,..., n) неравенство (2) не выполняется при t t_0.

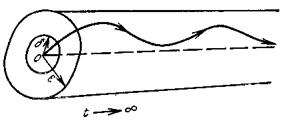Если устойчивое решение у_i^* (t), (i = 1, 2,..., n) при t → ∞ удовлетворяет условию

lim | у_i^* (t) - у_i (t) | = 0(t → ∞)

для всякого решения у_i (t), то в этом случае мы имеем дело с асимптотической устойчивостью (рисунок 3.6 – двумерный случай).

Устойчивость по Ляпунову – это устойчивость для достаточно малых начальных отклонений. Это существенно для исследования физической осуществимости состояния равновесия. Если данное состояние устойчиво по Ляпунову, то оно физически осуществимо, если нет – то неосуществимо, так как при любых сколь угодно малых начальных отклонениях изображающая точка системы начнет уходить из окрестности точки равновесия (пример: состояние маятника в верхнем положении - достаточно малого толчка, чтобы он уходил от нее все больше и больше).

Пример. Автопилот – прибор, который может многократно изменять положение рулей и тем самым изменять характер полета самолета. Пилоту задается цель (место и время прибытия), для достижения которой рассчитывается курс, пилот выводит самолет на расчетный курс и включает автопилот. Движение самолета будет описываться некоторой системой дифференциальных уравнений

z ' = f (z, t, p, ξ). (1)

Здесь z - вектор, описывающий фазовое состояние системы, т.е. координаты и скорость самолета, ξ – случайный вектор, характеризующий внешние воздействия, р – вектор конструктивных параметров автопилота, которые могут выбираться субъектом (конструктором), чтобы автопилот обеспечивал достижение цели управления.

Зная расчетную траекторию самолета, мы всегда можем выбирать начало отсчета таким образом, чтобы этой траектории при отсутствии внешних возмущений отвечали нулевые значения фазовых переменных. Значит, точка z = 0должна удовлетворять уравнению

f (0, t, p, 0) = 0.

Предположим далее, что в некоторый момент t = t₀ на движение самолета подействовало некоторое случайное возмущение (например, порыв ветра), в результате которого состояние системы изменилось:

z (t ₀) = z ₀ ≠ 0.

Каким условиям должно удовлетворять движение самолета, чтобы, несмотря на возмущение, он достиг заданной цели? Так как траектория самолета должна пройти через цель управления, то необходимо, чтобы возникшее отклонение параметров полета самолета от расчетных значений со временем могло исчезнуть. Для этого достаточно, чтобы движение самолета обладало асимптотической устойчивостью. Последнее означает, что должно выполняться условие

lim z(t) → 0 (t →∞) (2)

Это условие описывает асимптотические свойства движения при t →∞. Достижение цели должно произойти за конечное время Т. Здесь произошла замена большого, но конечного отрезка времени бесконечным. Возможность такой замены конечного отрезка времени бесконечным означает, что характерное время полета самолета является "практически" бесконечно большим: оно гораздо больше времени, необходимого для компенсации возмущения (характерного времени затухания колебаний самолета).

Исследование устойчивости тривиального решения (z =0) решается методами теории устойчивости.

Но задача проектирования автопилота, обеспечивающего асимптотическую устойчивость движения самолета, не сводится только к задаче теории устойчивости. Необходимо определить допустимые интервалы изменения параметров автопилота (компоненты вектора р), обеспечивающие устойчивость, т.е. решать обратную задачу. Поскольку отклонения от расчетной траектории – величины малые, то естественно использовать для решения рассматриваемой задачи идеи линеаризации.

Таким образом, изучая способы управления некоторым процессом, мы должны решать сразу две задачи: выбор принципиальной схемы регулятора (автопилота или какого либо другого механизма) и затем выбор его параметров, обеспечивающих достижение целей управления. Условия устойчивости определяют в пространстве параметров некоторое множество G₁. Выбор р G₁ гарантирует выполнение условия устойчивости (2).

Конструктивная схема накладывает на выбор параметров р вполне определенные ограничения р ∈ G₂. Значит для достижения цели управления, т.е. выполнения условий (2) (асимптотические свойства движения при ), необходимо, чтобы

р ∈ G₂ = G₁ ∩ G₂.

В распоряжении имеется множество параметров в области G, обеспечивающих достижение цели управления. Поэтому имеется возможность уточнения вектора р – возможность подчинить его каким-либо дополнительным условиям но уже не на множестве G₂, а на множестве G. Например, это может быть требование минимизации перегрузок (комфорт). Если достижение цели возможно многими способами, то появляется возможность обеспечить это условие. Тогда задачу оценки качества регулирования можно сформулировать следующим образом: на множестве параметров р, удовлетворяющих условию р G, найти такие значения р, которые обеспечивают выполнение условия

I(p) → min,

где I(p) – некоторый функционал, зависящий от траектории и характеризующий дополнительное ограничение (допустимую перегрузку).

В такой постановке рассматриваются процессы, развивающиеся на большом интервале времени, и применяются методы теории устойчивости, оперирующей с асимптотическими свойствами решений (при t → ∞): время полета самолета на много порядков больше времени компенсации его отдельных колебательных движений.