Как следует из закона Кулона, сила, действующая на точечный заряд q в электрическом поле, созданном другими зарядами, является центральной. Напомним, что центральной называется сила, линия действия которой направлена по радиус-вектору, соединяющему некоторую неподвижную точку О (центр поля) с любой точкой траектории. Из «Механики» известно, что все центральные силы являются потенциальными. Работа этих сил не зависит от формы пути перемещения тела, на которое они действуют, и равна нулю по любому замкнутому контуру (пути перемещения). В применении к электростатическому полю (рис.2.10):
 .
.
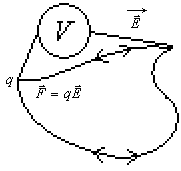
Рис.2.10. К определению работы сил электростатического поля.
То есть, работа сил поля по перемещению заряда q из точки 1 в точку 2 равна по величине и противоположна по знаку работе по перемещению заряда из точки 2 в точку 1, независимо формы пути перемещения. Следовательно, работа сил поля по перемещению заряда может быть представлена разностью потенциальных энергий заряда в начальной и конечной точках пути перемещения:  .
.
Введем потенциал электростатического поля φ, задав его как отношение: 
 , (размерность в СИ:
, (размерность в СИ:  ).
).
Тогда работа сил поля по перемещению точечного заряда q из точки 1 в точку 2 будет:
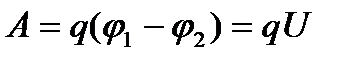
Разность потенциалов  называется электрическим напряжением. Размерность напряжения, как и потенциала, [U] = B.
называется электрическим напряжением. Размерность напряжения, как и потенциала, [U] = B.
Считается, что на бесконечности электрические поля отсутствуют, и значит  . Это позволяет дать определение потенциала как работы, которую нужно совершить, чтобы переместить заряд q = +1 из бесконечности в данную точку пространства. Таким образом, потенциал электрического поля является его энергетической характеристикой
. Это позволяет дать определение потенциала как работы, которую нужно совершить, чтобы переместить заряд q = +1 из бесконечности в данную точку пространства. Таким образом, потенциал электрического поля является его энергетической характеристикой
4.7 1.7. Связь между напряженностью и потенциалом электрического поля. Градиент потенциала. Теорема о циркуляции электрического поля. 
Напряженность и потенциал – это две характеристики одного и того же объекта – электрического поля, поэтому между ними должна существовать функциональная связь. Действительно, работа сил поля по перемещению заряда q из одной точки пространства в другую может быть представлена двояким образом:
Откуда следует, что 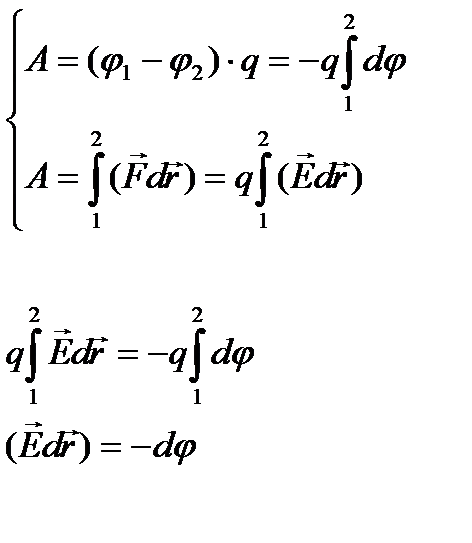
Или
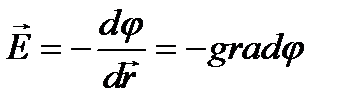
Это и есть искомая связь между напряженностью и потенциалом электрического поля в дифференциальном виде.
 - вектор, направленный из точки с меньшим потенциалом в точку с большим потенциалом (рис.2.11).
- вектор, направленный из точки с меньшим потенциалом в точку с большим потенциалом (рис.2.11).
,
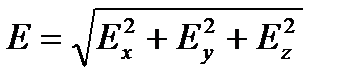
.
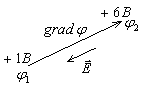
Рис.2.11. Векторы  и gradφ.
и gradφ.
Из свойства потенциальности электростатического поля следует, что работа сил поля по замкнутому контуру (φ1= φ2) равна нулю:  , поэтому можем написать
, поэтому можем написать 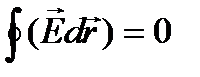
Последнее равенство отражает суть второй основной теоремы электростатики – теоремы о циркуляцииэлектрического поля, согласно которой циркуляция поля  вдоль произвольного замкнутого контура равна нулю. Эта теорема является прямым следствием потенциальности электростатического поля.
вдоль произвольного замкнутого контура равна нулю. Эта теорема является прямым следствием потенциальности электростатического поля.

 .
.
 .
.
 , (размерность в СИ:
, (размерность в СИ:  ).
).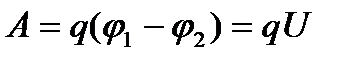
 называется электрическим напряжением. Размерность напряжения, как и потенциала, [U] = B.
называется электрическим напряжением. Размерность напряжения, как и потенциала, [U] = B. . Это позволяет дать определение потенциала как работы, которую нужно совершить, чтобы переместить заряд q = +1 из бесконечности в данную точку пространства. Таким образом, потенциал электрического поля является его энергетической характеристикой
. Это позволяет дать определение потенциала как работы, которую нужно совершить, чтобы переместить заряд q = +1 из бесконечности в данную точку пространства. Таким образом, потенциал электрического поля является его энергетической характеристикой
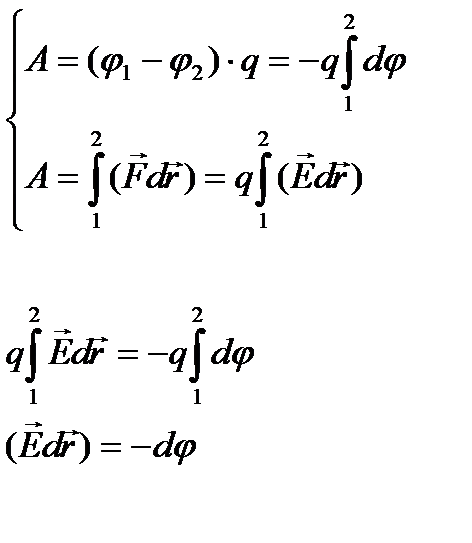
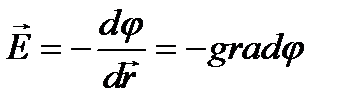
 - вектор, направленный из точки с меньшим потенциалом в точку с большим потенциалом (рис.2.11).
- вектор, направленный из точки с меньшим потенциалом в точку с большим потенциалом (рис.2.11).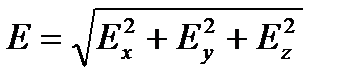 .
.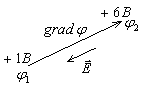
 и gradφ.
и gradφ. , поэтому можем написать
, поэтому можем написать 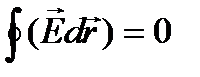
 вдоль произвольного замкнутого контура равна нулю. Эта теорема является прямым следствием потенциальности электростатического поля.
вдоль произвольного замкнутого контура равна нулю. Эта теорема является прямым следствием потенциальности электростатического поля.