XIX олимпиада по математике имени В. А.Курова 2020 - 2021 уч. год.

8класс

№ 1.	Докажите, что ни при каком целом значении n дроб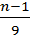и  и  не могут быть одновременно целыми числами.
№ 2.	Цена билета для входа на стадион была 180 рублей. После снижения входной платы число зрителей увеличилось на 50%, а выручка выросла на 25%. Сколько стоил билет после снижения входной платы?
№ 3.	Упростите выражение .
№ 4.	Стороны параллелограмма равны 8 и 3, биссектрисы двух углов параллелограмма, прилежащих к большей стороне, делят противолежащую сторону на три части. Найдите каждую из них.
№ 5.	В выпуклом семиугольнике проведите как можно больше диагоналей так, чтобы никакие три из них не были сторонами одного треугольника, вершины которого находятся в вершинах исходного семиугольника.

Оргкомитет олимпиады

 

XIX олимпиада по математике имени В. А.Курова

2020 - 2021 уч. год.

 

8класс

Решение

1. Пусть  тогда

n – 1 = 9q,

n + 4 = 12p.

Исключив n, получим 12p – 9q = 5. Если бы p и qбыли целыми, то левая часть равенства была бы кратна 3, но правая не кратна 3. Следовательно, p и q не могут быть целыми числами.

2. 150 р

3. 2

4. 3,2,3

5. В выпуклом семиугольнике проведите как можно больше диагоналей так, чтобы никакие три из них не были сторонами одного треугольника, вершины которого находятся в вершинах исходного семиугольника.

Решение:Диагональ семиугольника назовем «короткой», если она отсекает от

Короткая диагональ

семиугольника треугольник; в противном случае назовем ее «длинной». Понятно, что из каждой вершины семиугольник выходят 2 коротких и 2 длинных диагонали. Значит всего имеется 7 коротких и 7 длинных диагоналей. Легко заметить, что запрещенные в условии задачи треугольники можно составить только из одной длинной и двух коротких диагоналей. Если в семиугольнике проведены все 14 диагоналей, то всего имеется 7 запрещенных треугольников.     Теперь очевидно, что наша задача эквивалентна следующей: вычеркнуть как можно меньше диагоналей так, чтобы разрушить все запрещенные треугольники. Ясно, что вычеркивание одной длинной диагонали разрушает всего один запрещенный треугольник, а вычеркивание одной короткой диагонали разрушает 2 запрещенных треугольника. Поэтому трех вычеркиваний недостаточно, чтобы разрушить все запрещенные треугольники. Четырех вычеркиваний хватит, если действовать следующим образом. Вычеркнем последовательно 3 коротких диагонали так, чтобы каждый раз разрушались два новых запрещенных треугольника. Для разрушения последнего оставшегося запрещенного треугольника вычеркнем любую его сторону. ОТВЕТ: 10.