Контрольные задания по разделу

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ №1

И КОНТРОЛЬНЫЕ ЗАДАНИЯ

ПО ДИСЦИПЛИНЕ ЛИНЕЙНАЯ АЛГЕБРА (МАТЕМАТИКА)

“Нет ничего невозможного для людей”.

(Квинт Гораций Флакк (65-8 до н. э.) – древнеримский поэт)

“Нам не пристало падать духом”.

(Марк Туллий Цицерон (106-43 до н. э.) – древнеримский политический деятель, оратор и писатель)

“Нет ничего, что не преодолевалось бы трудом”.

(Джордано Бруно (1548-1600) – итальянский философ и поэт)

При выполнении контрольной работы следует руководствоваться следующими требованиями.

1. Работа должна быть представлена в срок, установленный графиком учебного процесса.

2. Работа должна быть правильно оформлена и выполнена четким, разборчивым почерком без применения сокращений слов. Страницы должны быть пронумерованы и иметь поля для замечаний преподавателя.

3. В начале работы должен быть указан номер варианта. Номер варианта работы соответствует номеру фамилии студента в журнале учебной группы.

4. Последовательность изложения решений задач должна соответствовать их номерам в задании.

5. Перед решением задач необходимо указать их номер и полностью привести условие задания.

6. Решение задания должно завершаться ответом с указанием искомых величин и их значений.

7. Решение задач следует представлять в развернутом виде с краткими пояснениями и подробными арифметическими расчетами. При этом сначала необходимо привести определение и выражение для вычисления искомой характеристики. Задачи, в которых приводятся только ответы без промежуточных вычислений, считаются нерешенными.

8. Титульный лист работы должен быть корректно оформлен.

Студенты, не выполнившие контрольную работу или не устранившие замечания преподавателя, к сдаче зачета не допускаются.

Контрольные задания по разделу

“Линейная алгебра”

Задание 1.

Найти матрицу А, равную матричному выражению. Указать размеры матрицы А.

Таблица 1. Варианты задания 1

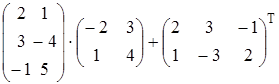
1)	2)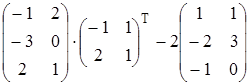
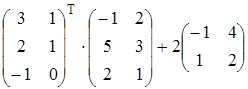
3)	4)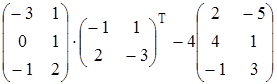
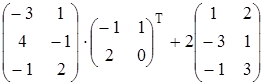
5)	6)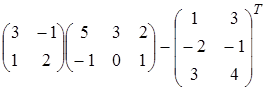
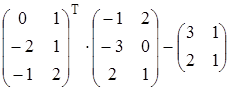
7)	8)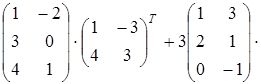
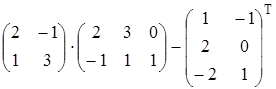
9)	10)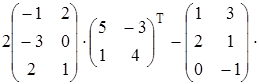
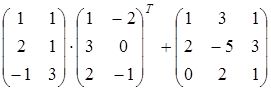
11)	12)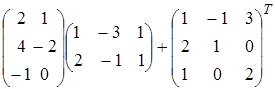
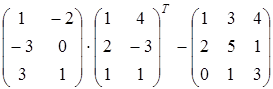
13)	14)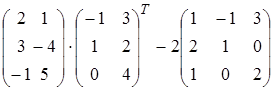
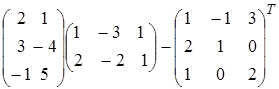
15)	16)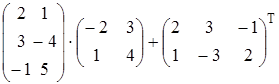
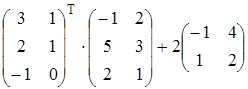
17)	18)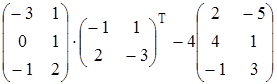
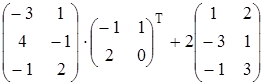
19)	20)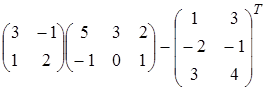
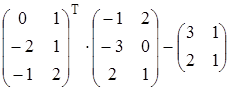
21)	22)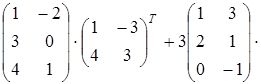
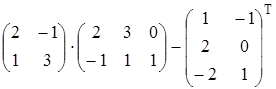
23)	24)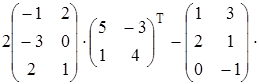
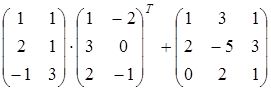
25)	26)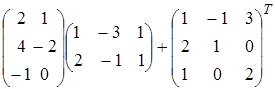
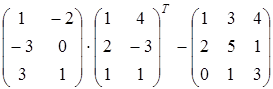
27)	28)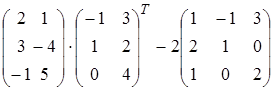
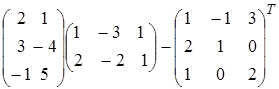
29)	30)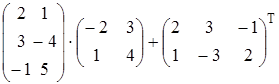

Задание 2.

Вычислить определитель матрицы А с помощью теоремы Лапласа (разложением по элементам строки или столбца). Предварительно выполнить преобразование определителя с целью получения четырех равных нулю элементов в этой строке (столбце). Таким образом, вычисление определителя 5-го порядка сводится к расчёту одного определителя 4-го порядка. Далее аналогично свести к расчету одного определителя 3-го порядка. Затем одного определителя 2-го порядка.

Таблица 2. Варианты задания 2

Вариант	Матрица А	Вариант	Матрица А

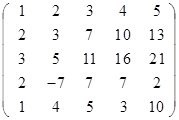
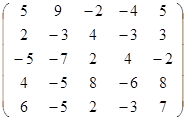
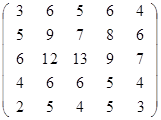
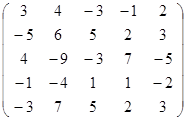
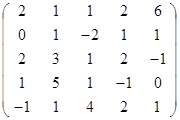
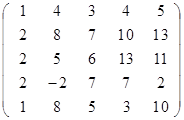
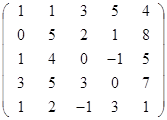
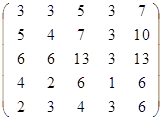
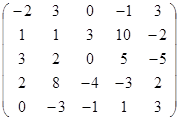
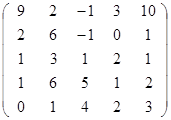
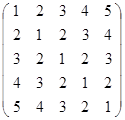
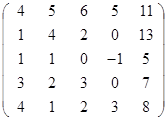
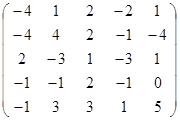
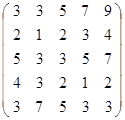
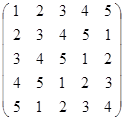
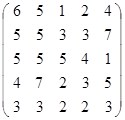
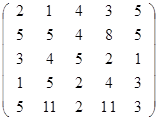
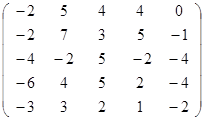
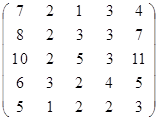
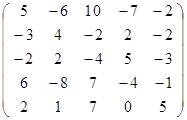
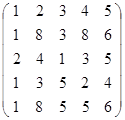
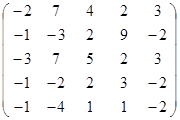
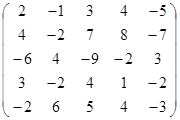
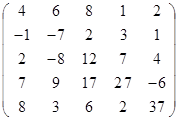
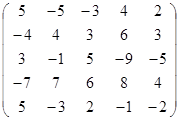
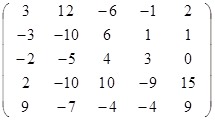
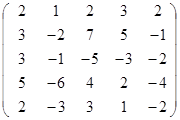
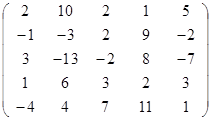
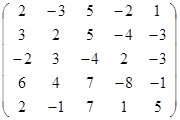
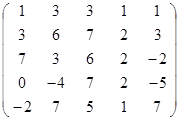
Задание 3.

Дана матрица А (табл. 3). Найти обратную матрицу А^-1.

Выполнить проверку: А А^-1 = Е.

Таблица 3. Варианты задания 3

Вариант	Матрица А	Вариант	Матрица А

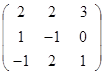
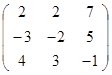
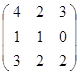
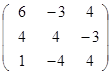
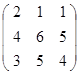
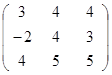
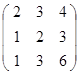
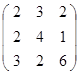
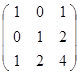
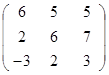
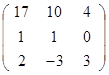
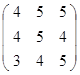
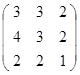
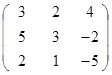
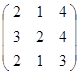
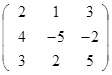
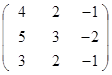
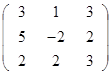
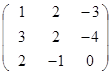
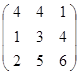
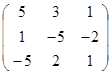
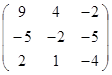
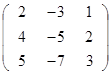
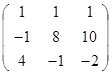
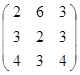
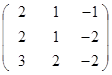
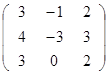
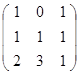
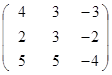
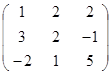
Задание 4.

Найти решение системы линейных алгебраических уравнений (табл. 4) матричным способом с помощью обратной матрицы. Выполнить проверку полученного решения. Представить графическую иллюстрацию решения системы: построить прямые, соотнести график с результатом решения матричным способом.

Таблица 4. Варианты задания 4

Вариант	Система линейных уравнений	Вариант	Система линейных уравнений

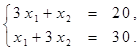
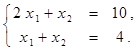
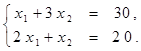
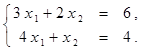
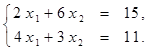
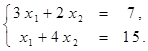
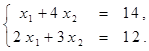
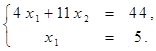
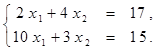
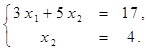
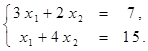
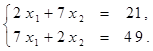
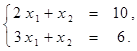
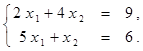
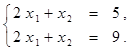
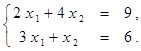
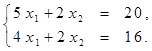
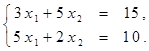
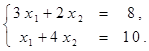
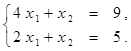
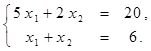
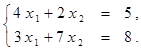
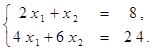
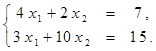
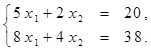
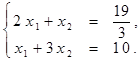
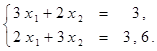
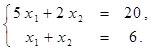
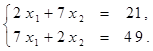
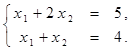
Задание 5.

Найти решение системы линейных алгебраических уравнений (табл. 5) двумя способами:

1) методом Крамера,

2) методом Гаусса.

Таблица 5. Варианты задания 5

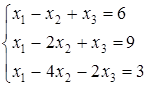
1)	2)	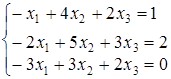3)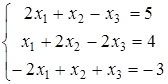
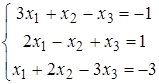
4)	5)	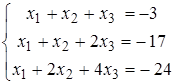6)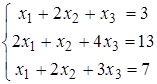
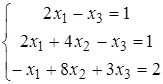
7)	8)	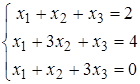9)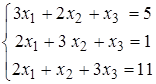
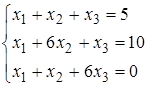
10)	11)	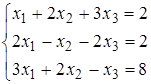12)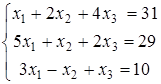
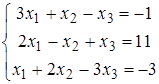
13)	14)	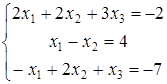15)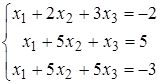
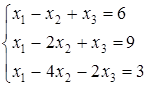
16)	17)	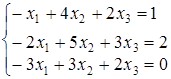18)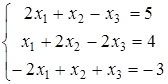
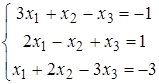
19)	20)	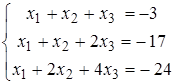21)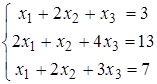
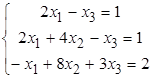
22)	23	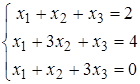24)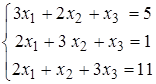
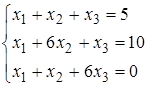
25)	26)	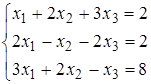27)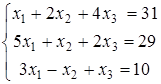
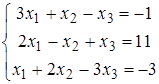
28)	29)	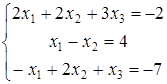30)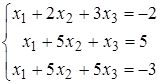

Задание 6.

Построить кривые второго порядка (окружность, эллипс, параболу) по заданным уравнениям (табл. 6).

Таблица 6. Варианты задания 6

Вариант	Уравнения	Вариант	Уравнения
	, , .		, , .
	, , .		, , .
	, , .		, , .
	, , .		, , .
	, , .		, , .
	, , .		, , .
	, , .		, , .
	, , .		, , .
	, , .		, , .
	, , .		, , .
	, , .		, , .
	, , .		, , .
	, , .		, , .
	, , .		, , .
	, , .		, , .

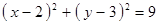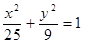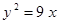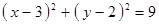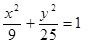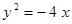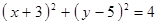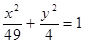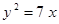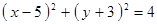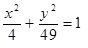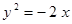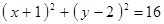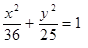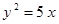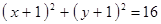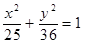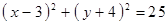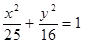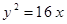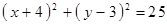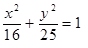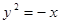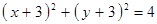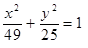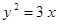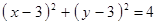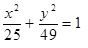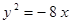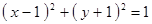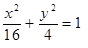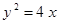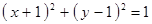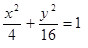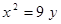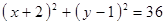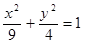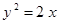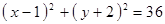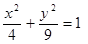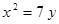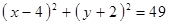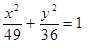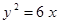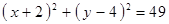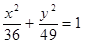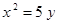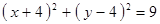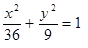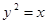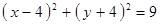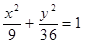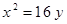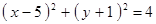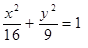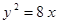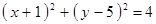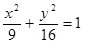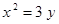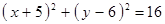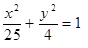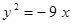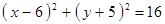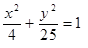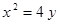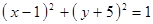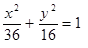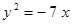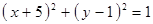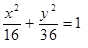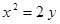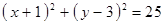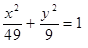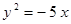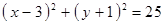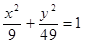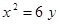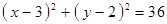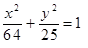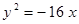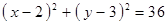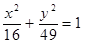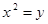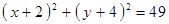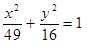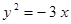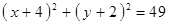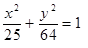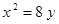СПИСОК ЛИТЕРАТУРЫ

1. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономических специальностей: учебник и практикум (части I и II) / Под ред. Н.Ш. Кремера. – 2-е изд., перераб. и доп. - М.: Высшее образование, 2007. – 893 с.

2. Кузнецов Б.Т. Математика: учебник для студентов вузов, обучающихся по специальностям экономики и управления (060000). – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2004. – 719 с.

3. Сборник задач и упражнений по высшей математике: Математическое программирование: учебное пособие / А.В. Кузнецов, В.А. Сакович, Н.И. Холод и др.; Под общ. ред. А.В. Кузнецова, Р.А. Рутковского. – 2-е изд., перераб. и доп. – Минск: Вышэйшая школа, 2002. – 447 с.

4. Сборник задач по высшей математике для экономистов: учебное пособие / Под ред. В.И. Ермакова. – М.: ИНФРА-М, 2002. – 575 с.

5. Справочник по математике для экономистов: учебное пособие / Под ред. В.И. Ермакова. – 3-е изд., перераб. и доп. – М.: ИНФРА-М, 2007. 464 с.