Геометрические характеристики плоских сечений

РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ СТЕРЖНЕВОЙ

СИСТЕМЫ

Задание. Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням с помощью шарниров.

Требуется:

1) найти усилия и напряжения в стержнях, выразив их через силу Q;

2) найти допускаемую нагрузку 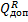, приравняв большее из напряжений в двух стержнях расчетному сопротивлению R = 210 МПа;

3) найти допускаемую нагрузку по предельному равновесию, если предел текучести = 240 МПа;

4) сравнить полученные величины допускаемых нагрузок.

Дано: A = 16 cм2; a = 2,7 м; b = 2,6 м; c = 1,8 м; k = 2.

Р е ш е н и е.

1 Рассмотрим геометрическую сторону задачи. Для этого покажем схему деформирования заданной системы, обозначим буквами характерные точки абсолютно жесткого бруса и пронумеруем стержни.

Абсолютно жесткий брус под действием нагрузки Q повернется относительно шарнирной опоры O по часовой стрелке на угол α. Принимая угол очень малым, видим, что первый стержень станет короче на величину ∆l₁ = CD, а второй – длиннее на ∆ l₂ = OF. Из подобия треугольников ACD и OAF получим

2 Рассмотрим статическую сторону задачи. Покажем все силы, действующие на абсолютно жесткий брус. Направления усилий N1 и N2 определяем по схеме деформирования/

Здесь неизвестными являются усилия N1, N2, а также две составляющие реакции опоры S. Общее число неизвестных равно четырем. Для решения задачи можно составить только три независимых уравнения равновесия:

Следовательно, задача один раз статически неопределимая. В качестве дополнительного уравнения будем использовать уравнение совместности деформаций.

3 Рассмотрим физическую сторону задачи. В уравнении выразим деформации через усилия по закону Гука:

Подставив исходные данные E₁ = E₂, A₂ = 2A₁, l₂ =1,8, l₁ = 2,7,, получим

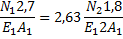
4 Для определения N1 и N2 решим совместно уравнения:

5 Составим выражения для напряжений в стержнях:

6 Сравним полученные напряжения: >

Напряжение в первом стержне получилось больше, чем во втором.

7 Определим допускаемую нагрузку из условия прочности наиболее напряженного стержня, в данном случае второго:

=R

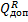=210/10/0,0326=644 Н

8 Рассмотрим предельное равновесие системы, полагая, что

и

9 Сравним полученные значения

Вывод: допускаемая нагрузка, полученная по предельному равновесию, в 1,4 раза выше допускаемой нагрузки, найденной по расчетному сопротивлению.

Задача 4

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

Задание. Для поперечного сечения, требуется: 1) определить положение центра тяжести; 2) найти осевые и центробежный моменты инерции относительно случайных центральных осей; 3) определить направления главных центральных осей; 4) найти моменты инерции относительно главных центральных осей; 5) вычертить сечение в масштабе 1: 2 и указать на нем все оси и размеры в числах. Данные взять из табл. 4.1.

Р е ш е н и е.

Для заданных стандартных профилей приведем справочные данные. Все размеры на рисунках указаны в мм.

Уголок № 100×100×8;

F =15,6 см²; I_x = I_y = 147,2 см⁴; I_x0 =233,3 см⁴; I_y0 = 60,2 см⁴;

см^4’

Двутвавр № 22а;

F =32,8 см²; I_x = 206 см⁴ ; I_y = 2790 см⁴; I_yx = 0 см⁴

Найдем центр тяжести заданного сечения в координатах x₁, y₁:

Через точку С (x1 =8,34; y1 = 4,11) проводим взаимно перпендикулярные координатные оси x, y. Относительно осей x, y находим координаты точек C1,С2. Получаем: C1 (8,64; 5,59); С2 (-4,11; -2,66).

Проверяем положение центра тяжести:

S_x =15,6⋅(5,59)+32,8⋅(-2,66) = 0,024≈ 0; ∆= 0,2 %;

S_y =15,6⋅(8,64)+32,8⋅(-4,11) = 0,044 ≈ 0; ∆= 0,4 %.

Статические моменты относительно осей x, y получились близкими к нулю, следовательно, точка пересечения осей x, y является центром тяжести, а сами оси x, y – случайными центральными осями заданного сечения.

Вычисляем моменты инерции относительно осей x, y:

I_x =147,2+15,6⋅(5,59)² +2790+32,8(-2,66)² = 3592 см⁴;

I_y =147,2+15,6⋅(-8,64)² +206+32,8⋅(-4,11)² = 2072см⁴;

I_xy = −86,55+15,6⋅(8,64)⋅(5,59)+32,8⋅(-4,11)⋅(-2,66) = 1025 см⁴.

Найдем положение главных центральных осей:

α=-26,7

sin α = - 0,450; cos α = 0,893; sin 2α = - 0,803; cos 2α = 0,596; sin ²α = 0,202; cos ²α = 0,798

Поворачивая оси x, y против часовой стрелки на угол α = 17,1, получаем главные центральные оси u, v.

Найдем главные центральные моменты инерции:

I_u = 3592∙0,798+2072∙0,202 -(1025)(-0,803)= 4108 см⁴.

I_v = 3592∙0,202+2072∙0,798+(1025)(-0,803)= 1556 см⁴.

Проверка:

I_u+ I_v= I_x+ I_y

3592 + 2072=4108+1556;

5664=5664

I_uv=(3592-2072)/2∙(-0,803)+(1025)∙0,596=0

Задача 5