 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства определенного интеграла. Df. Промежуток с гранич. т
|
|
Df. Промежуток с гранич. т. A и B ориентированным, если указано направление перехода от т. A к т. B.
1. Пусть сущ. определенный интеграл  сущ. определенный интеграл
сущ. определенный интеграл  и справедливо равенство
и справедливо равенство

2. 
Док-во:


3. Свойство линейности определенного интеграла:
1. Пустьф-ии  интегрируемы на
интегрируемы на 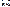 ***
***

2. Пусть  , то для любой произвольной постоянной
, то для любой произвольной постоянной 
 - справедлива формула
- справедлива формула 
4. Аддитивность определенного интеграла:
Пусть ф-ия  интегрируема на большем их трех помежутков
интегрируема на большем их трех помежутков  , тогда она интегрируема на обоих меньших промежутках и справедлива формула:
, тогда она интегрируема на обоих меньших промежутках и справедлива формула:
 Свойство монотонности.
1. Пусть ф-ия
Свойство монотонности.
1. Пусть ф-ия  неотрицательна на
неотрицательна на 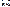 и интегрируема на нем,
и интегрируема на нем,  Док-во: В силу н-ва для ф-ий любая интегрируема ф-ия неотрицательна Þ любая последовательность интегрируемых сумм будет иметь неотрицательный предел Þ интеграл будет неотрицательным.
Док-во: В силу н-ва для ф-ий любая интегрируема ф-ия неотрицательна Þ любая последовательность интегрируемых сумм будет иметь неотрицательный предел Þ интеграл будет неотрицательным.

 2. Пусть ф-ия
2. Пусть ф-ия  на
на 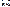 , искл. конечн. точек, и интегрируема на
, искл. конечн. точек, и интегрируема на 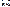 , тогда
, тогда 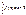 Док-во: Из интегрируемости следует, что предел не зависит от выбора разбиения на
Док-во: Из интегрируемости следует, что предел не зависит от выбора разбиения на 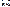 . Достаточно строить инт. разбиения так, чтобы точки, в которых ф-ия равна нулю, являлись точками разбиения. А следовательно в силу аддитивности интеграл по всему прмежутку равен сумме интегралов по частичным промежуткам, т.к ****
. Достаточно строить инт. разбиения так, чтобы точки, в которых ф-ия равна нулю, являлись точками разбиения. А следовательно в силу аддитивности интеграл по всему прмежутку равен сумме интегралов по частичным промежуткам, т.к ****
 Df Две ф-ии
Df Две ф-ии  , заданные на
, заданные на 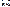 , значения которых различны на
, значения которых различны на 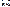 лишь в конечном ч. точек называются эквивалентными на этом отрезке.
3. Инт. от эквивалентных ф-ий совп.
Пусть
лишь в конечном ч. точек называются эквивалентными на этом отрезке.
3. Инт. от эквивалентных ф-ий совп.
Пусть  эквивалентны и интегрируемы на
эквивалентны и интегрируемы на  , тогда
, тогда  (они не совпадают а интегралы совпадают).
Д-во:
(они не совпадают а интегралы совпадают).
Д-во:
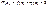 на
на 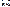 лишь в конеч. ч. точек отр.
лишь в конеч. ч. точек отр. 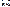 , следовательно по 2му
, следовательно по 2му 
 4. Пусть
4. Пусть  на
на 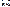 , кроме конечного ч. точек,
, кроме конечного ч. точек,  инт. на
инт. на 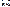 ,
, 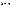 , то
, то 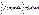 5. Пусть
5. Пусть  инт-ма на
инт-ма на 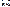 Þ модуль ф-ии тоже интегрируем на
Þ модуль ф-ии тоже интегрируем на 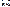 и справедливо неравенство:
и справедливо неравенство:
 6. Пусть
6. Пусть  интегрируема на
интегрируема на 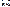 ,
, 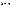 , то существует М, такая что
, то существует М, такая что  25.Интеграл с переменным верхним пределом.
Теорема о его непрерывности.
Теорма: Если функция f(x) интегрируема на отрезке [a,b], то функция
25.Интеграл с переменным верхним пределом.
Теорема о его непрерывности.
Теорма: Если функция f(x) интегрируема на отрезке [a,b], то функция
 непрерывна на этом отрезке.
Доказательство: Дадим числу х приращение ∆х так, чтобы х+∆хÎ[a,b]. Для наглядности изобразим на числовой оси один из возможных вариантов расположения точек:
непрерывна на этом отрезке.
Доказательство: Дадим числу х приращение ∆х так, чтобы х+∆хÎ[a,b]. Для наглядности изобразим на числовой оси один из возможных вариантов расположения точек:
 |
 |
a x0 x х+∆х b
 |
 |
Получим:
По теореме (Если функция y=f(x) интегрируема на отрезке, то интегрируема и абсолютная величина |f(x)|, причем
 |
…(на этом теорема закончилась, но неравенство относится к ней.) и следствию из теоремы (Если на отрезке [a,b] функция f(x) интегрируема и удовлетворяет неравенству m£f(x)£M. То выполняются неравенства:
(на этом следствие из теоремы закончилось)
получаем:
Отсюда следует, что при ∆х→0 будет ∆F→0. Это доказывает непрерывность функции F(x). Отметим, что для подынтегральной функции f(x) точка х может быть точкой разрыва.
Дата публикования: 2015-11-01; Прочитано: 197 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
