Примеры решения задач. Пример 1. Определить заряд Q, прошедший по проводу с сопро­тивлением R=3Ом при равномерном нарастании напряжения на концах провода от U0=2В до U =4В в течение

Пример 1. Определить заряд Q, прошедший по проводу с сопро­тивлением R= 3Ом при равномерном нарастании напряжения на концах провода от U ₀ = 2В до U = 4В в течение t= 20с.

Р е ш е н и е. Так как сила тока в проводе изменяется, то вос­пользоваться для подсчета заряда формулой Q=It нельзя. Поэтому возьмем дифференциал заряда d Q=Idt и проинтегрируем:

(1)

Выразив силу тока по закону Ома, получим

(2)

Напряжение U в данном случае переменное. В силу равномерности нарастания оно может быть выражено формулой

U= U ₀ +kt, (3)

где k - коэффициент пропорциональности. Подставив это выражение U в формулу (2), найдем

Проинтегрировав, получим

(4)

Значение коэффициента пропорциональности k найдем из формулы (3), если заметим, что при t= 20 с U= 4В:

k= (U-U ₀) /t= 0,1B/c.

Подставив значения величин вформулу (4), найдем

Q= 20Кл.

П р и м е р 2. Потенциометр с сопротивлением R = 100Ом подклю­чен к источнику тока, ЭДС ε которого равна 150 В и внутреннее со­противление r = 50 Ом (рис. 19.1). Определить показание вольтметра с сопротивлением R _B = 500Ом, соединенного проводником с одной из клемм потен­циометра и подвижным контактом с се­рединой обмотки потенциометра. Какова разность потенциалов между теми же точками потенциометра при отключен­ном вольтметре?

Р е ш е н и е. Показание U ₁ вольт­метра, подключенного к точкам А и В (рис. 19.1), определяется по формуле

U ₁ =I ₁ R ₁, (1)

где I ₁ - сила тока в неразветвленной, части цепи; R ₁- сопротивление параллельно соединенных вольтметра и половины потенциометра.

Силу тока I ₁ найдем по закону Ома для всей цепи:

I ₁ = ε/(R+r), (2)

где R - сопротивление внешней цепи.

Внешнее сопротивление R есть сумма двух сопротивлений:

R=R/2+R₁. (3)

Сопротивление R ₁параллельного соединения может быть най­дено по формуле откуда

R _l= RR _B /(R + 2 R _B).

Подставив в эту формулу числовые значения величин и произве­дя вычисления, найдем

R _l=45,5Ом.

Подставив в выражение (2) правую часть равенства (3), опреде­лим силу тока:

=1,03 А

Если подставить значения I ₁ и R ₁в формулу (1), то найдем пока­зание вольтметра: U ₁ = 46,9В.

Разность потенциалов между точками А и В при отключенном вольтметре равна произведению силы тока I ₂ на половину сопротивления потенциометра, т. е. U ₂ =I ₂ (R/ ₂), или

Подставив сюда значения величин ε, r и R получим

U ₂ = 50В.

Пример 3. Источники тока с электродвижущими силами ε ₁и ε ₂включены в цепь, как показано на рис. 19.2. Определить силы токов, текущих в сопротивлениях R ₂ и R ₃, если ε ₁ = 10 В иε₂ = 4В, а R ₁ =R ₄ = 20ми R ₂ =R ₃ = 4Ом. Сопротивлениями источников тока пренебречь.

Р е ш е н и е. Силы токов в разветвленной цепи определяют с помощью законов Кирхгофа. Чтобы найти четыре значения силы токов, следует составить четыре уравнения.

Указание. Перед составлением уравнений по закону Кирхгофа необхо­димо, во-первых, выбрать произвольно направления токов, текущих через сопротивления, указав их стрелками на чертеже, и, во-вторых, выбрать на­правление обхода контуров (последнее только для составления уравнений по второму закону Кирхгофа).

Выберем направления токов, как они показаны на рис. 19.2, и условимся обходить контуры по часовой стрелке.

Рассматриваемая в задаче схема имеет два узла: А и В. Но состав­лять уравнение по первому закону Кирхгофа следует только для одного узла, так как уравнение, составленное для второго узла, будет следствием первого уравнения.

При составлении уравнений по первому закону Кирхгофа необ­ходимо соблюдать правило знаков: ток, подходящий к узлу, входит в уравнение со знаком плюс; ток, отходящий от узла, - со знаком минус.

По первому закону Кирхгофа для узла В имеем

I ₁+ I ₂+ I ₃- I ₄=0.

Недостающие три уравнения получим по второму закону Кирхгофа. Число независимых уравнений, которые могут быть составле­ны по второму закону Кирхгофа, также меньше числа контуров (в нашем случае контуров шесть, а независимых уравнений три). Чтобы найти необходимое число независимых уравнений, следует придерживаться правила: выбирать контуры таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь, не участвовав­шая ни в одном из ранее использованных контуров.

При составлении уравнений по второму закону Кирхгофа необ­ходимо соблюдать следующее правило знаков:

а) если ток по направлению совпадает с выбранным направлени­ем обхода контуров, то соответствующее произведение IR входит в уравнение со знаком плюс, в противном случае произведение IR входит в уравнение со знаком минус,

б) если ЭДС повышает потенциал в направлении обхода контура, т.е. если при обходе контура приходится идти от минуса к плюсу внутри источника, то соответствующая ЭДС входит в уравнение со знаком плюс, в противном случае - со знаком минус.

По второму закону Кирхгофа имеем соответственно для контуров AR ₁ BR ₂ A, AR ₁ BR ₃ A, AR ₃ BR ₄ A:

I ₁ R ₁ - I ₂ R ₂ =ε ₁ - ε₂ (1)

I ₁ R ₁- I ₃ R ₃ = ε ₁ (2)

I ₃ R ₃ + I ₄ R ₄ = 0. (3)

Подставив в равенства (1)-(3) значения сопротивлений и ЭДС, получим систему уравнений:

I ₁ +I ₂ +I ₃ -I ₄ = 0,

2 I ₁ - 4 I ₂=6,

2 I ₁ - 4 I ₃=10,

4 I ₃ + 2 I ₄=0.

Поскольку нужно найти только два тока, то удобно воспользо­ваться методом определителей (детерминантов). С этой целью пере­пишем уравнения еще раз в следующем виде:

I ₁ +I ₂ +I ₃ -I ₄ = 0,

2 I ₁ - 4 I ₂+0+0=6,

2 I ₁+0 - 4 I ₃+0=10,

0+0+4 I ₃ + 2 I ₄=0.

Искомые значения токов найдем из выражений

I ₂ = Δ _{I 2}/Δи I ₃ = Δ_I3/Δ,

где Δ- определитель системы уравнений; Δ_I2и Δ_I3 - определители, полученные заменой соответствующих столбцов определителя А столбцами, составленными из свободных членов четырех вышеприведенных уравнений, находим

Отсюда получаем

I ₂=0; I ₃ = -1 А.

Знак минус у значения силы тока I ₃ свидетельствует о том, что при произвольном выборе направлений токов, указанных на рисунке, направление тока I ₃было указано противоположно истинному. На самом деле ток I ₃ те­чет от узла В к узлу А.

Пример 4. Сила тока в про­воднике сопротивлением R= 20 Ом нарастает в течение вре­мени Δt=2 с по линейному за. кону от I ₀=0 до I _max=6 А (рис. 19.3). Определить количество теплоты Q ₁, выделившееся в этом проводнике за первую секунду, и Q ₂ - за вторую, а также найти отношение этих количеств теплоты Q ₂/ Q ₁.

Р е ш е н и е. Закон Джоуля - Ленца Q= I ² Rt применим в случае постоянного тока (I =const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде

d Q= I ² R d t. (1)

Здесь сила тока I является некоторой функцией времени. В на­шем случае

I=kt, (2)

где k - коэффициент пропорциональности, равный отношению приращений силы тока к интервалу времени, за который произошло это приращение:

k= Δ I/ Δ t.

С учетом равенства (2) формула (1) примет вид

d Q=k ² Rt ²d t. (3)

Для определения количества теплоты, выделившегося за конечный промежуток времени Δ t, выражение (3) следует проинтегрировать в пределах от t ₁до t ₂:

При определении количества теплоты, выделившегося за первую секунду, пределы интегрирования t ₁=О, t ₂ = 1 с и, следовательно,

Q ₁=60 Дж,

а за вторую секунду - пределы интегрирования t ₁= 1 с, t ₂ =2 с и тогда

Q₂=420 Дж.

Следовательно,

Q ₂/ Q ₁ =7,

т. е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую секунду.

Задачи

Закон Ома для участка цепи

19.1. Сила тока в проводнике равномерно нарастает от I ₀=0 до I =3 А в течение времени t =10c. Определить заряд Q, прошедший в проводнике.

19.2. Определить плотность тока j в железном проводнике длиной, l = 10 м, если провод находится под напряжением U =6 В.

19.3. Напряжение U на шинах электростанции равно 6,6 кВ. Потребитель находится на расстоянии l= 10 км. Определить площадь S сечения медного провода, который следует взять для уст­ройства двухпроводной линии передачи, если сила тока I в линии равна 20 А и потери напряжения в проводах не должны превышать 3 %.

19.4. Вычислить сопротивление R графитового проводника, изготовленного в виде прямого кругового усеченного конуса высотой h= 20см и радиусами оснований, r ₁ = 12 мм и r ₂=8 мм. Температура t проводника равна 20 ˚С.

19.5. На одном конце цилиндрического медного проводника со­противлением R ₀ = 10 Ом' (при 0 ˚С) поддерживается температура t ₁ = 20˚С, на другом t ₂ = 400 ˚С. Найти сопротивление R проводника, счи­тая градиент температуры вдоль егооси постоянным.

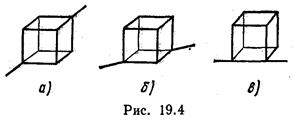
19.6. Проволочный куб составлен из проводников. Сопротивление R ₁ каждого проводника, составляюще­го ребро куба, равно 1 Ом. Вычислить сопротивление R этогоку­ба, если он включен в электрическую цепь, как показано на рис. 19.4, а.

19.7. То же (см. задачу 19.6), если куб включен в цепь, как показано на рис. 19.4, б,

19.8. То же (см. задачу 19.6), если куб включен в цепь, как показано на рис. 19.4, в.

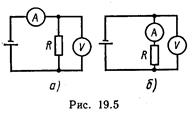
19.9. Катушка и амперметр соединены последовательно и присоединены к источнику тока. К зажимам катушки присоединен вольтметр сопротивлением R _В= 1 кOм. Показания амперметра I= 0,5 А,вольтметра U= 100В. Определить сопротивление R катушки. Сколько процентов от точного значения сопротивления катушки составит погрешность, если не учитывать сопротивления вольтмет­ра?

19.10. Зашунтированный амперметр измеряет токи силой до I = 10 А. Какую наибольшую силу тока может измерить этот ампер­метр без ш у нта, если сопротивле­ние R _а амперметра равно 0,02 Ом и сопротивление R _шшунта равно 5 мOм?

19.11. Какая из схем, изобра­женных на рис. 19.5, а, б, более пригодна для измерения больших сопротивлений и какая - для измерения малых сопротивлений? Вычислить погрешность, допус­каемую при измерении с помощью этих схем сопротивлений R _l =1 кOм и R ₂ = 10Ом. Принять сопротивления вольтметра R_B и амперметра R _а соответственно равными 5 кОм и 2 Ом.

Закон Ома для всей цепи

19.12. Внутреннее сопротивление r батареи аккумуляторов рав­но 3 Ом. Сколько процентов от точного значения ЭДС составляет погрешность, если, измеряя разность потенциалов на зажимах ба­тареи вольтметром с сопротивлением R_В=200 Ом, принять ее рав­ной ЭДС?

19.13. К источнику тока с ЭДС ε= 1,5В присоединили катуш­ку с сопротивлением R= 0,1Ом. Амперметр показал силу тока, рав­ную I ₁=0,5 А. Когда к источнику тока присоединили последова­тельно еще один источник тока с такой же ЭДС, то сила тока I в той же катушке оказалась равной 0,4 А. Определить внутренние сопротивления r ₁ и r ₂ первого и второго источников тока.

19.14. Две группы из трех последовательно соединенных элементов соединены параллельно. ЭДС ε каждого элемента равна 1,2 В, внутреннее сопротивление r =0,2 Ом. Полученная батарея замкнута на внешнее сопротивление R= 1,5 Ом. Найти силу тока I во внеш­ней цепи.

19.15. Имеется N одинаковых гальванических элементов с ЭДС ε и внутренним сопротивлением r _i каждый. Из этих элемен­тов требуется собрать батарею, состоящую из нескольких параллель­но соединенных групп, содержащих по n последовательно соединен­ных элементов. При каком значении n сила тока I во внешней цепи, имеющей сопротивление R, будет максимальной? Чему будет равно внутреннее сопротивление Ri батареи при этом значении п?

19.16. Даны 12 элементов с ЭДС ε= 1,5 В и внутренним сопро­тивлением r= 0,4Ом. Как нужно соединить эти элементы, чтобы получить от собранной из них батареи наибольшую силу тока во внешней цепи, имеющей сопротивление R= 0,3Ом? Определить максимальную силу тока I _max.

19.17. Два одинаковых источника тока с ЭДС ε= 1,2 В и внутренним сопротивлением r =0,4 Ом соединены, как показано на рис. 19.6, а, б. Определить силу тока I в цепи и разность потенциалов U между точками А и В в первом и втором случаях.

19.18. Два элемента (ε ₁ = 1,2В, r ₁=0,1 Ом; ε ₂ = 0,9В, r ₂=0,3 Ом) соединены одноименными полюсами. Сопротивление R соединительных проводов равно 0,2 Ом. Определить силу тока I в цепи.

Правила Кирхгофа

19.19. Две батареи аккумуляторов (ε ₁ = 10В, r ₁=1 Ом; ε ₂=8 В, r ₂=2 Ом) и реостат (R= 6Ом) соединены, как показано на рис. 19.7. Найти силу тока в батареях и реостате.

19.20. Два источника тока (ε ₁ = 8 В, r ₁=2 Ом; ε ₂ = 6В, r ₂= 1,5 Ом) и реостат (R= 10 Ом) соединены, как показано на рис. 19.8. Вычислить силу тока I, текущего через реостат.

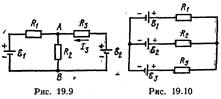
19.21. Определить силу тока I ₃ в резисторе сопротивлением R ₃(рис.19.9) и напряжение U ₃на концах резистора, если ε ₁ = 4В, ε ₂ = 3В, R ₁ = 2 Ом, R ₂ = 6Ом, R ₃=1 Ом. Внутренними сопротивле­ниями источников тока пренебречь.

19.22. Три батареи с ЭДС ε ₁ = 12 В, ε ₂ = 5 В и ε= 10 В и одина­ковыми внутренними сопротивлениями r, равными 1 Ом, соединены между собой одноименными полюсами. Сопротивление соединитель­ных проводов ничтожно мало. Определить силы токов I, идущих че­рез каждую батарею.

19.23. Три источника тока с ЭДC ε ₁ = 11 В, ε ₂ = 4 В и ε ₃ = 6 В и три реостата с сопротивлениями R ₁ = 5Ом, R ₂=10 Ом и R ₃ = 2Ом соединены, как показано на рис. 19.10. определить силы токов I в реостатах. Внутреннее сопротивление источника тока пренебрежимо мало.

19.24. Тpи сопротивления R _l=5 Ом, R ₂ = 1Ом и R ₃=3 Ом, а так­же источник тока с ЭДС ε ₁=1,4 В

соединены, как показано на рис. 19.11. определить ЭДС ε источника тока, который надо подключить в цепь между точками А и В, чтобы в сопротивлении R ₃ шел ток силой I = 1 А в направлении, указанном стрелкой. Сопротивлением источника тока пренебречь.

Работа и мощность тока

19.25. Лампочка и реостат, соединенные последовательно присоединены к источнику тока. Напряжение U на зажимах лампочки равно 40 В, сопротивление R реостата равно 10 Ом. Внешняя цепь потребляет мощность Р= 120Вт. Найти силу тока I в цепи.

19.26. ЭДС батареи аккумуляторов ε =12 В, сила тока I ко­роткого замыкания равна 5 А. Какую наибольшую мощность Р _max можно получить во внешней цепи, соединенной с такой батареей?

19.27. К батарее аккумуляторов, ЭДС ε которой равна 2 В и внутреннее сопротивление r= 0,5 Ом, присоединен проводник. Определить: 1) сопротивление R проводника, при котором мощность, выделяемая в нем, максимальна; 2) мощность Р, которая при этом выделяется в проводнике.

19.28. ЭДС ε батареи равна 20 В. Сопротивление R внешней цепи равно 2 Oм, сила тока I =4 А. Найти КПД батареи. При каком значении вешнего сопротивления R КПД будет равен 99%?

19.29. К зажимам батареи аккумуляторов присоединен нагреватель. ЭДC ε батареи равна 24 В. Внутреннее сопротивление r =1 Ом. Нагреватель, включенный в цепь, потребляет мощность P =80 Вт. Вычислить силу тока I в цепи и КПД η нагревателя.

19.30. Обмотка электрического кипятильника имеет две секции. Если включена только первая секция, то вода закипает через t ₁ = 15 мин, если только вторая, то через t ₂=30 мин. Через сколько минут закипит вода, если обе секции включить последовательно? параллельно?

19.31. При силе тока I ₁=3 Аво внешней цепи аккумулятора выделяется мощность Р ₁=18 Вт, при силе тока I ₂=1 А- со-

ответственно Р ₂ = 10 Вт. Определить ЭДС - ε и внутреннее сопротивление r батареи.

­19.32. Сила тока в проводнике сопротивлением r= 100Ом равномерно нарастает от I ₀=0 до I _max=10 А в течение времени τ =30 с. Определить количество теплоты Q, выделившееся за это время в про­воднике,

19.33. Сила тока в проводнике сопротивлением R= 12 Ом равномерно убывает от I ₀ = 5А до I= 0в течение времени t= 10 с. Какое количество теплоты Q выделяется в этом проводнике за указанный промежуток времени?

19.34. По проводнику сопротивлением R= 3Ом течет ток, сила которого возрастает. Количество теплоты Q, выделившееся в проводнике за, время τ=8 с, равно 200 Дж. Определить количество электричества q, протекшее за это время по проводник. В момент времени, принятый за начальный, сила тока в проводнике равна нулю.

19.35. Сила тока в проводнике сопротивлением R= 15 Ом равномерно возрастает от I ₀=0 до некоторого максимального значения в течение времени τ=5 с. За это время в проводнике выделилось количество теплоты Q =10 кДж. Найти среднюю силу тока < I> в проводнике за этот промежуток времени.

19.36. Сила тока в проводнике равномерно увеличивается от I ₀=0 до до некоторого максимального значения в течение времени τ=10 с. За это время в проводнике выделилось количество теплоты Q= 1кДж. Определить скорость нарастания тока в проводнике, если сопротивление R его равно 3 Ом.