 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Тема: Машина Тюрінга
|
|
1) Поняття Машини Т’юрінга.
2) Конструювання Машини Т’юрінга.
3) Обчислюваність функцій на Машині Т’юрінга.
4) Теза Т’юрінга.
Введення поняття Машини Т’юрінга було однією з перших вдалих спроб дати точне з математичної точки зору визначення поняття алгоритму. Це поняття було назване на честь математика Т’юрінга, який у 1937 році сформулював дане поняття. Машина Т’юрінга є математичною, уявною машиною, а не фізичною. Машина Т’юрінга це такий самий математичний об’єкт як похідна, інтеграл, функція. Так як і інше математичне поняття, Машина Т’юрінга відображає об’єктивну реальність, моделює деякі реальні процеси. Машина Т’юрінга представляє собою систему, що працює в дискретні моменти часу t = 0,1,2… і складається з наступних частин:
1) Скінченної стрічки, що розбита на скінчену кількість комірок. При цьому в кожний момент часу t в комірках записані букви з деякого алфавіту  , що називають зовнішнім алфавітом машини Т’юрінга. Комірка в якій записаний символ 0 називається пустою. В процесі роботи машини кожна комірка може змінювати свій стан, шляхом заміни приписаного до неї символа
, що називають зовнішнім алфавітом машини Т’юрінга. Комірка в якій записаний символ 0 називається пустою. В процесі роботи машини кожна комірка може змінювати свій стан, шляхом заміни приписаного до неї символа 
 на інший символ
на інший символ  . До існуючої комірки дозволяється прибудовувати необмежене число додаткових комірок, які початково вважаються пустими. Стрічка вважається направленою і її комірки будуть переглядатися зліва направо. Таким чином, якщо в деякий момент часу стрічка має r комірок, то стан стрічки повністю описується словом
. До існуючої комірки дозволяється прибудовувати необмежене число додаткових комірок, які початково вважаються пустими. Стрічка вважається направленою і її комірки будуть переглядатися зліва направо. Таким чином, якщо в деякий момент часу стрічка має r комірок, то стан стрічки повністю описується словом 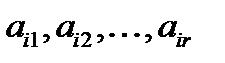 , де
, де  – це стан першої комірки,
– це стан першої комірки,  – стан другої комірки і так далі.
– стан другої комірки і так далі.
2) Управляюча каретка, що представляю собою пристрій, що переміщується вздовж стрічки так, що в кожен момент часу, що розглядається, вона знаходиться навпроти визначеної комірки і має деякий стан  з множини станів Q ={
з множини станів Q ={  }. Множина
}. Множина  називається множиною внутрішніх станів. Множини А і Q не перетинаються, їх перетин є пустою множиною.
називається множиною внутрішніх станів. Множини А і Q не перетинаються, їх перетин є пустою множиною.
Стан  називається заключним, а стан
називається заключним, а стан 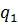 – початковим, даний стан означає початок роботи машини.
– початковим, даний стан означає початок роботи машини.
3) Програми П, тобто сукупності виразів T(i, j),  . Команда T(i, j) з якої будується програма, складається з команд трьох видів:
. Команда T(i, j) з якої будується програма, складається з команд трьох видів:
1) 

2) 

3) 

Команда з початком  спрацьовує, якщо машина М знаходиться в стані
спрацьовує, якщо машина М знаходиться в стані  , а каретка оглядає символ
, а каретка оглядає символ  . Тому в програмі повинна бути тільки одна команда з початком
. Тому в програмі повинна бути тільки одна команда з початком  . Дії при виконанні вище зазначених команд наступні:
. Дії при виконанні вище зазначених команд наступні:
1) 
 при виконанні даної команди машина Т’юрінга переходить до стану
при виконанні даної команди машина Т’юрінга переходить до стану  , одночасно змінюючи символ, який оглядається на
, одночасно змінюючи символ, який оглядається на  . В командах даного типу символ С – означає, що далі буде оглядатися ця ж комірка.
. В командах даного типу символ С – означає, що далі буде оглядатися ця ж комірка.
2) 
 при виконанні даної команди машина Т’юрінга переходить до стану
при виконанні даної команди машина Т’юрінга переходить до стану  , одночасно змінюючи символ, який оглядається на
, одночасно змінюючи символ, який оглядається на  . В командах даного типу символ R – означає, що каретка переміщується на одну комірку праворуч.
. В командах даного типу символ R – означає, що каретка переміщується на одну комірку праворуч.
3) 
 при виконанні даної команди машина Т’юрінга переходить до стану
при виконанні даної команди машина Т’юрінга переходить до стану  , одночасно змінюючи символ, який оглядається на
, одночасно змінюючи символ, який оглядається на  . В командах даного типу символ L – означає, що каретка переміщується на одну комірку ліворуч.
. В командах даного типу символ L – означає, що каретка переміщується на одну комірку ліворуч.
Зауваження: стани  ,
,  можуть співпадати, і стани
можуть співпадати, і стани  також.
також.
Як працює машина Т’юринга?
Знаходячись в момент стану t в стані відмінному від  машина здійснює крок, який повністю визначається її поточним станом
машина здійснює крок, який повністю визначається її поточним станом  і символом
і символом  , який оглядає в даний момент каретка. При цьому зміст кроку регламентований командою
, який оглядає в даний момент каретка. При цьому зміст кроку регламентований командою  :
: 
 , де Х є {C, L, R}.
, де Х є {C, L, R}.
Крок полягає в тому, що:
1) Зміст комірки  що оглядається в даний момент часу витирається і на його місце записується символ
що оглядається в даний момент часу витирається і на його місце записується символ  , який може співпадати з
, який може співпадати з  .
.
2) Машина переходить в новий стан  , який може співпадати з
, який може співпадати з  .
.
3) Машина переходить до перегляду наступної комірки, що розміщується ліворуч, якщо X=L і до комірки, що розміщується праворуч, якщо X=R, та продовжує оглядати ту саму комірку якщо X=C.
В наступний момент часу t+1, якщо 
 , машина виконує крок, що регламентований командою
, машина виконує крок, що регламентований командою  і т.д. Процедура переходу така ж сама.
і т.д. Процедура переходу така ж сама.
Словом в алфавіті А або в алфавіті Q або в об’єднаному алфавіті  називається будь-яка послідовність букв відповідного алфавіту. Під
називається будь-яка послідовність букв відповідного алфавіту. Під
к–ю конфігурацією будемо розуміти зображення стрічки машини з інформацією, що склалася на ній до початку к-го кроку з вказівкою комірки, яка оглядається на даному кроці і вказівкою стану, в якому знаходиться машина. Конфігурація називається заключною або кінцевою, якщо стан, в якому знаходиться машина є заключним. Робота машини Т’юрінга вважається закінченою, якщо досягається кінцева конфігурація, яка і є результом роботи машини.
Будемо вважати, що не пусте слово  в алфавіті
в алфавіті  \
\  сприймається машиною в стандартному положенні. Якщо дане слово записане у послідовно розміщені комірки стрічки, всі інші комірки пусті і машина оглядає крайню комірку праворуч, в яких записане слово
сприймається машиною в стандартному положенні. Якщо дане слово записане у послідовно розміщені комірки стрічки, всі інші комірки пусті і машина оглядає крайню комірку праворуч, в яких записане слово  .
.
Стандартне положення називається початковим (кінцевим), якщо машина сприймає слово в стандартному положенні і знаходиться в початковому стані  (в стані зупинки
(в стані зупинки  ).
).
Приклад 1.
Задана машина Т’юринга із зовнішнім алфавітом  (0 – символ пустої комірки), алфавітом внутрішніх станів
(0 – символ пустої комірки), алфавітом внутрішніх станів  і з наступною функціональною схемою (програмою):
і з наступною функціональною схемою (програмою):
 .
.
Розглянемо в яке слово перетворює задана машина слово 101.
Робота машини починається з стандартного положення
Положення 1
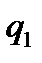
Крок 1 
Положення 2

Крок 2 
Положення 3

Крок 3 
Положення 4

Дана конфігурація є заключною, так як машина опинилась у стані зупинки  .
.
Таким чином, вхідне слово 101 перероблено машиною в слово 10101.
Отриману послідовність конфігурацій можна записати більш коротким способом. Конфігурація (1) записується у вигляді наступного слова в алфавіті  :
:  (зміст комірки, що оглядається, записується праворуч від стану, в якому знаходиться в даний момент машина).
(зміст комірки, що оглядається, записується праворуч від стану, в якому знаходиться в даний момент машина).
Аналогічно, конфігурація (2):  ; конфігурація (3):
; конфігурація (3): 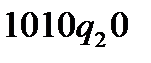 ;
;
конфігурація (4):  . Вся послідовність записується наступним чином:
. Вся послідовність записується наступним чином:  .
.
Приклад 2.
Визначати послідовність команд, що визначає послідовність конфігурацій машини Т’юринга, яка переробляє слово 11011, виходячи з початкового положення, в якому в стані  оглядається крайня ліва непуста комірка, в якій розміщений символ даного слова
оглядається крайня ліва непуста комірка, в якій розміщений символ даного слова
(1)

(2)

(3)

(4)

(5)

(6)

(7)
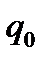
Опис машини Т’юринга:
Зовнішній алфавіт  (0-символ пустої комірки).
(0-символ пустої комірки).
Алфавіт внутрішніх станів  .
.
Програма П:
 .
.
Біль короткий запис послідовності конфігурацій:

 .
.
Приклад 3.
Машина Т’юринга задається зовнішнім алфавітом  , (0 – символ пустої комірки). Алфавітом внутрішніх станів
, (0 – символ пустої комірки). Алфавітом внутрішніх станів  і програмою П;
і програмою П;

 ,
,
 .
.
Програма може бути записана також у вигляді наступної таблиці:

| 
| 
| 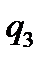
| |
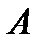
| ||||

| 
| 
| ||

| 
| 
| ||
| * | 
| 
| 
|
Для того, щоб визначити дії машини в кожний конкретний момент часу, треба знайти в таблиці клітку, що знаходиться на перетині поточного стану машини (стовпчик  ) і рядка, в якому міститься значення комірки, що оглядається в поточний момент часу (
) і рядка, в якому міститься значення комірки, що оглядається в поточний момент часу ( ).
).
Застосуємо дану машину до слова 11*11.Вхідна конфігурація стандартна. Послідовність конфігурацій наступна:





 .
.
Самостійно застосувати машину Т’юринга з прикладу 3 до наступних початкових конфігурацій:  .
.
Дана машина Т’юринга реалізує операцію додавання. В результаті її роботи на стрічці записано послідовно стільки одиниць, скільки їх було записано послідовно по обидві сторони від знака “*” перед початком роботи машини.
Будемо казати, що слово  переробляється машиною у слово
переробляється машиною у слово  , якщо від слова
, якщо від слова  , яке сприймається в початковому стандартному положенні машина після виконання скінченного числа команд переходить до слова
, яке сприймається в початковому стандартному положенні машина після виконання скінченного числа команд переходить до слова  , що сприймається машиною в положенні зупинки.
, що сприймається машиною в положенні зупинки.
Висновок 1:
Машина Т’юринга – це деяке правило (алгоритм) для перетворення слів з алфавіту  .
.
Висновок 2:
Для визначення машини Т’юринга необхідно задати зовнішній та внутрішній алфавіти, програму, і вказати які з символів позначають пусту комірку та кінцевий (заключний) стан.
Дата публикования: 2015-11-01; Прочитано: 1589 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
