Вычитание и сложение

Примеры

Разложим число =3,14159265… в непрерывную дробь и подсчитаем его подходящие дроби:

3, 22/7, 333/106, 355/113, 103993/33102, …

Вторая подходящая дробь 22/7 — это известное архимедово приближение. Четвёртая подходящая дробь 355/113 была впервые получена в Древнем Китае.

В теории музыки требуется отыскать рациональное приближение для . Третья подходящая дробь 7/12 позволяет обосновать классическое делениеоктавы на 12 полутонов^[3].

Свойства и примеры

Любое рациональное число может быть представлено в виде конечной цепной дроби двумя способами, например:

Теорема Лагранжа: Число представляется в виде бесконечной периодической цепной дроби тогда и только тогда, когда оно является иррациональным решением квадратного уравнения с целыми коэффициентами.

Например:

золотое сечение

Для алгебраических чисел степени большей 2 характер разложений в непрерывную дробь неизвестен. Например, даже для неизвестно, конечно ли количество различных чисел в его разложении (последовательность A002945 в OEIS).

Для некоторых трансцендентных чисел можно найти простую закономерность. Например, для основания натурального логарифма:

для числа

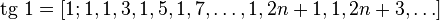
У числа пи простой закономерности не видно^[4]:

Теорема Гаусса — Кузьмина: Почти для всех (кроме множества меры нуль) вещественных чисел существует среднее геометрическое коэффициентов соответствующих им цепных дробей, и оно равно постоянной Хинчина.

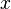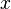Теорема Маршалла Холла. Если в разложении числа в непрерывную дробь, начиная со второго элемента не встречаются числа большие , то говорят, что число относится к классу . Любое вещественное число может быть представлено в виде суммы двух чисел из класса и в виде произведения двух чисел из класса ^[5] В дальнейшем было показано, что любое вещественное число может быть представлено в виде суммы трёх чисел из класса и в виде суммы четырёх чисел из класса . Количество требуемых слагаемых в этой теореме не может быть уменьшено — для представления некоторых чисел указанным образом меньшего количества слагаемых недостаточно.^[6][7]

Правила знаков

Минус и плюс – это признаки отрицательных и положительных чисел в математике. Они по-разному взаимодействую с собой, поэтому при выполнении каких-либо действий с числами, например, деление, умножение, вычитание, сложение и т.д., необходимо учитывать правила знаков. Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.

Рассмотрим подробней основные правила знаков.

Деление.

Если мы делим «плюс» на «минус», то получаем всегда «минус». Если мы делим «минус» на «плюс», то получаем всегда также «минус». Если мы делим «плюс» на «плюс», то получаем «плюс». Если же мы делим «минус» на «минус», то получим, как ни странно, также «плюс».

Умножение.

Если мы умножаем «минус» на «плюс», то получаем всегда «минус». Если мы умножаем «плюс» на «минус», то получаем всегда также «минус». Если мы умножаем «плюс» на «плюс», то получаем положительно число, то есть «плюс». Тоже самое касается и двух отрицательных чисел. Если мы умножаем «минус» на «минус», то получим «плюс».

Вычитание и сложение.

Они базируются уже на других принципах. Если отрицательное число будет больше по модулю, чем наше положительное, то результат, конечно же, будет отрицательный. Наверняка, вам интересно, что же такое модуль и зачем он тут вообще. Все очень просто. Модуль – это значение числа, но без знака. Например -7 и 3. По модулю -7 будет просто 7, а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.