Алгебраические линии

Алгебраические линии – линии, которые могут быть заданы алгебраическим уравнением, т.е. уравнением, в котором общая часть приведена к виду многочлена, целого относительно текущих координат.

Окружность (отрезок d) – плоская кривая второго порядка, ортогональная проекция которой может быть окружностью (рисунок 4.6 а) и эллипсом (рисунок 4.6 б). Для изображения окружности диаметра d на комплексном чертеже обязательно строят проекции центра О и двух ее диаметров. Удобнее всего строить проекции диаметров, параллельных плоскостям проекций: АВ||П_1;; CD||П₂, CD^П₁ (рисунок 4.6 б). Фронтальная проекция окружности – эллипс – определяется малой осью эллипса A₂B₂= d*cos β и большой осью эллипса C₂D₂=d.

Если плоскость окружности наклонена ко всем основным плоскостям проекций, то все три ее проекции есть эллипсы, которые можно построить по сопряженным диаметрам, являющимся проекциями тех диаметров окружности, которые параллельны плоскостям проекций.

а)	б)

Рисунок 4.6

Эллипс – замкнутая плоская кривая второго порядка, для которой сумма расстояний от любой ее точки до двух точек-фокусов есть величина постоянная, равная большой оси эллипса.

Существует несколько способов построения эллипса. Можно построить эллипс по его большой АВ и малой CD осям (рисунок 4.7).

Рисунок 4.7	Рисунок 4.8

На осях эллипса, как на диаметрах, строят две окружности, которые нужно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности – прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса.

Парабола – плоская незамкнутая кривая второго порядка, все точки которой равно удалены от данной точки – фокуса и от данной прямой – директрисы. Параболу можно построить по её вершине О и заданной точке В, принадлежащей параболе (рисунок 4.8). Для этого строят прямоугольник ОАВС и делят его стороны на равные части. Из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.

Можно построить параболу как кривую, касательную к прямым с заданными на них точками А и В (рисунок 4.9). Стороны угла, образованного этими прямыми, делят на равные части и нумеруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую этих прямых.

Гипербола – плоская незамкнутая кривая второго порядка, состоящая из двух ветвей, концы которых удаляются в бесконечность (стремясь к своим асимптотам).

Рисунок 4.9	a) Рисунок 4.10

Каждая точка гиперболы обладает следующим свойством: разность ее расстояний от двух данных точек – фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Гипербола, асимптоты которой взаимно перпендикулярны, называется равнобокой. Она широко применяется для построения диаграмм, когда задана своими координатами одна ее точка М (рисунок 4.10, а). Тогда через заданную точку проводят линии А В и KL параллельно координатным осям. Из начала координат проводят серию лучей, пересекающих линии АВ и KL. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.

Лемниската Бернулли – на оси АВ (рисунок 4.10, б) строим две окружности, касательные в точке О. Проводим диаметр РР¢. Через точки Р и О проводим касательные лемнискаты. От точки В на окружности откладываем расстояние ВК, затем KL = KB. Из точки О радиусом OL засекаем прямую ОВ в точке М. Из точки М восстанавливаем перпендикуляр MN. Радиусом ON засекаем прямую OK в точке 1. Так же получаем остальные точки лемнискаты. Симметричные точки строятся простым переносом. Применяется в дорожном строительстве и в нефтяной промышленности при определении движения жидкости между двумя скважинами.

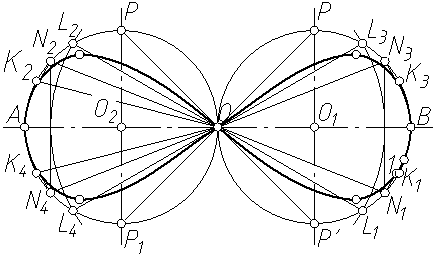
б)

Рисунок 4.10