 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Контрольная работа. Аналитическая геометрия ТЕМА 3. Аналитическая геометрия
|
|
Контрольная работа
Аналитическая геометрия ТЕМА 3. Аналитическая геометрия
1. Уравнения линии в декартовой системе координат.
2. Параметрические уравнения линии.
3. Плоскость, прямая на плоскости и в пространстве.
4. Линии второго порядка.
Решение типового варианта контрольной работы
Задача №1.
Даны три последовательные вершины параллелограмма А(2;-3), В(5;1),С(3;-4). Не находя координаты вершины D, найти:
1) уравнение стороны AD;
2) уравнение высоты BK, опущенной из вершины В на сторону AD;
3) длину высоты BK;
4) уравнение диагонали BD;
5) тангенс угла между диагоналями параллелограмма.
Записать общие уравнения найденных прямых. Построить чертеж.
Решение.
Сначала построим чертеж. Построим в прямоугольной декартовой системе координат точки 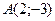 ,
, 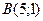 ,
, 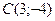 . Построим отрезки
. Построим отрезки 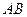 и
и 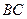 .
.
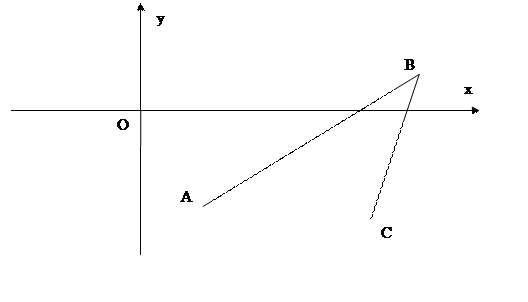
Рис. 1
Достроим полученный рисунок до параллелограмма и нанесем на чертеж высоту BK.
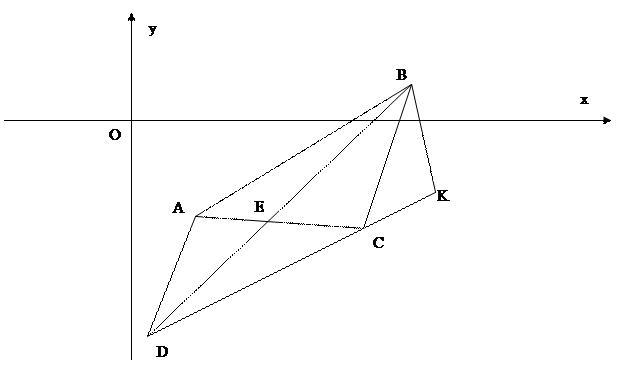
Рис. 2
1) Составим уравнение прямой AD.
а) Предварительно найдем уравнение прямой BС. Уравнение прямой, проходящей через точки  и
и 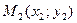 , имеет вид
, имеет вид
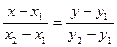 (3.1)
(3.1)
По условию 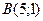 ,
, 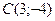 . Подставим координаты точек
. Подставим координаты точек 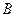 и
и 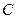 в уравнение (3.1):
в уравнение (3.1): 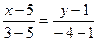 , т.е.
, т.е. 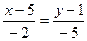 .
.
Запишем полученное уравнение в общем виде, то есть в виде 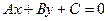 . Для этого в последнем уравнении избавимся от знаменателей
. Для этого в последнем уравнении избавимся от знаменателей 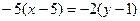 и проведем преобразования, перенося все слагаемые в левую часть равенства:
и проведем преобразования, перенося все слагаемые в левую часть равенства: 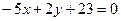 или
или 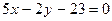 .
.
Из этого уравнения выразим 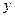 :
: 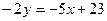 ;
; 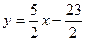 . Получили уравнение вида
. Получили уравнение вида 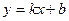 - уравнение с угловым коэффициентом.
- уравнение с угловым коэффициентом.
б) Воспользуемся тем фактом, что противоположные стороны параллелограмма параллельны. Составим искомое уравнение прямой AD как уравнение прямой, проходящей через точку 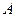 параллельно прямой
параллельно прямой 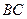 .
.
Уравнение прямой, проходящей через данную точку 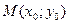 в данном направлении, имеет вид
в данном направлении, имеет вид
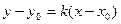 (3.2)
(3.2)
где направление определяется угловым коэффициентом 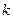 .
.
Условие параллельности двух прямых 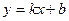 и
и 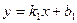 имеет вид
имеет вид
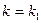 (3.3)
(3.3)
По условию задачи 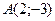 , прямая
, прямая 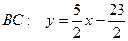 . Подставим координаты точки
. Подставим координаты точки 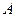 в уравнение (3.2):
в уравнение (3.2): 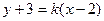 . Так как прямая
. Так как прямая 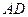 параллельна прямой
параллельна прямой 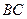 , то в силу формулы (3.3) их угловые коэффициенты совпадают. Угловой коэффициент прямой
, то в силу формулы (3.3) их угловые коэффициенты совпадают. Угловой коэффициент прямой 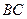 равен
равен 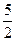 , следовательно, уравнение прямой
, следовательно, уравнение прямой 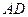 имеет вид
имеет вид 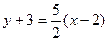 .
.
Запишем уравнение прямой 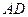 в общем виде. Для этого раскроем скобки и все слагаемые перенесем в левую часть равенства:
в общем виде. Для этого раскроем скобки и все слагаемые перенесем в левую часть равенства: 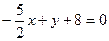 . Умножим обе часть равенства на (-2) и получим общее уравнение прямой
. Умножим обе часть равенства на (-2) и получим общее уравнение прямой 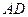 :
: 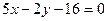 .
.
Запишем уравнение прямой 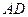 в виде с угловым коэффициентом. Для этого выразим
в виде с угловым коэффициентом. Для этого выразим 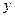 из общего уравнения:
из общего уравнения: 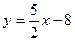 .
.
2) Составим уравнение высоты 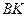 , проведенной из вершины
, проведенной из вершины 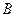 на сторону
на сторону 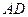 как уравнение прямой, проходящей через точку
как уравнение прямой, проходящей через точку 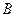 перпендикулярно прямой
перпендикулярно прямой 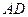 .
.
Условие перпендикулярности двух прямых 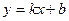 и
и 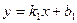 имеет вид
имеет вид
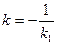 (3.4)
(3.4)
Подставим координаты точки 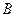 в уравнение (3.2):
в уравнение (3.2): 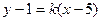 . Так как высота
. Так как высота 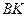 перпендикулярна прямой
перпендикулярна прямой 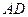 , то их угловые коэффициенты связаны соотношением (3.4). Угловой коэффициент прямой
, то их угловые коэффициенты связаны соотношением (3.4). Угловой коэффициент прямой 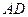 равен
равен 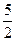 , следовательно, угловой коэффициент высоты
, следовательно, угловой коэффициент высоты 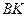 равен
равен 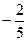 и уравнение прямой
и уравнение прямой 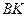 имеет вид
имеет вид 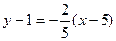 . Запишем уравнение высоты
. Запишем уравнение высоты 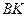 в общем виде:
в общем виде: 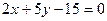 . Запишем это же уравнение в виде с угловым коэффициентом:
. Запишем это же уравнение в виде с угловым коэффициентом: 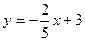 .
.
3) Найдем длину высоты 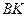 как расстояние от точки
как расстояние от точки 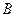 до прямой
до прямой 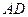 .
.
Расстояние 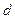 от точки
от точки 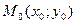 до прямой
до прямой 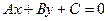 представляет собой длину перпендикуляра, опущенного из точки на прямую и определяется формулой
представляет собой длину перпендикуляра, опущенного из точки на прямую и определяется формулой
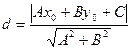 (3.5)
(3.5)
Так как 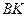 перпендикулярна
перпендикулярна 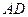 , то длина
, то длина 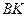 может быть найдена с помощью формулы (3.5). По условию
может быть найдена с помощью формулы (3.5). По условию 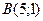 , прямая
, прямая 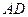 определяется уравнением
определяется уравнением 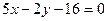 . В силу формулы (3.5) длина высоты
. В силу формулы (3.5) длина высоты 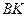 равна
равна 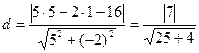 =
= 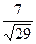 .
.
4) Найдем уравнение диагонали 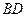 как уравнение прямой, проходящей через точки
как уравнение прямой, проходящей через точки 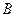 и
и 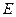 , где
, где 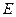 - середина отрезка
- середина отрезка 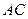 .
.
а) Если 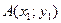 и
и 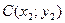 , то координаты точки
, то координаты точки 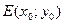 - середины отрезка
- середины отрезка 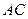 , определяются формулами
, определяются формулами
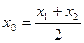
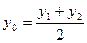 (3.6)
(3.6)
По условию 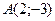 ,
, 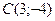 . В силу формул (3.6) имеем:
. В силу формул (3.6) имеем: 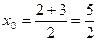 ,
, 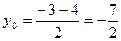 . Следовательно
. Следовательно 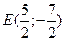 .
.
б) Так как точка пересечения диагоналей является их серединой, то точка 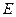 (середина отрезка
(середина отрезка 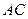 ) является точкой пересечения диагоналей и диагональ
) является точкой пересечения диагоналей и диагональ 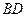 проходит через точку
проходит через точку 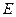 .
.
Воспользуемся уравнением (3.1). По условию 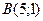 ,
, 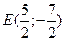 . В силу формулы (3.1) уравнение прямой
. В силу формулы (3.1) уравнение прямой 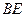 (диагонали
(диагонали 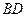 ) имеет вид:
) имеет вид: 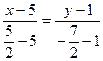 или
или 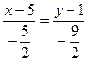 . Запишем это уравнение в общем виде:
. Запишем это уравнение в общем виде: 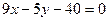 . Запишем это же уравнение в виде с угловым коэффициентом:
. Запишем это же уравнение в виде с угловым коэффициентом: 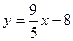 .
.
5) Найдем тангенс угла между диагоналями 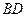 и
и 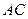 .
.
а) Найдем уравнение диагонали 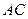 как уравнение прямой, проходящей через две данные точки.
как уравнение прямой, проходящей через две данные точки.
Воспользуемся уравнением (3.1). По условию 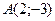 ,
, 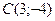 . Следовательно,
. Следовательно, 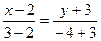 . Общее уравнение диагонали
. Общее уравнение диагонали 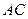 имеет вид
имеет вид 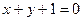 , уравнение с угловым коэффициентом – вид
, уравнение с угловым коэффициентом – вид 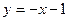 , угловой коэффициент
, угловой коэффициент 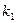 прямой
прямой 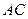 равен
равен 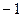 .
.
б) Уравнение диагонали 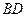 имеет вид
имеет вид 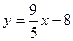 , ее угловой коэффициент
, ее угловой коэффициент 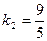 .
.
в) Тангенс угла 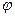 между прямыми
между прямыми 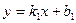 и
и 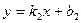 определяется формулой
определяется формулой
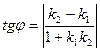
Следовательно, 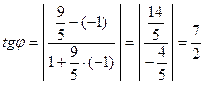 . Отсюда
. Отсюда 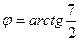 .
.
Задача №2.
Условие задачи №2 несколько различается в зависимости от номера варианта контрольной работы. Приведем решения простейших задач, входящих в это задание.
1) Составить уравнение плоскости, проходящей через точки 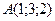 ,
, 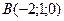 ,
, 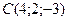 .
.
Решение.
Уравнение плоскости, проходящей через точки 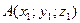 ,
, 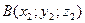 ,
, 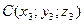 имеет вид:
имеет вид:
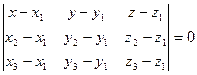 (3.7)
(3.7)
Тогда уравнение плоскости 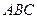 в силу уравнения (3.7) имеет вид
в силу уравнения (3.7) имеет вид 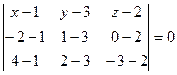 или
или 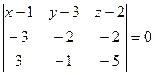 .
.
Запишем полученное уравнение в общем виде, т.е. в виде 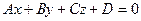 . Для этого раскроем определитель по первой строке
. Для этого раскроем определитель по первой строке 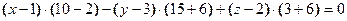 . После преобразований получим:
. После преобразований получим: 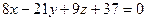 .
.
2) Найти нормальный вектор плоскости 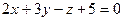 .
.
Решение.
Нормальный вектор 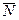 - это вектор, перпендикулярный плоскости. Если плоскость задана общим уравнением
- это вектор, перпендикулярный плоскости. Если плоскость задана общим уравнением 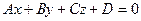 , то нормальный вектор имеет координаты
, то нормальный вектор имеет координаты 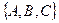 .
.
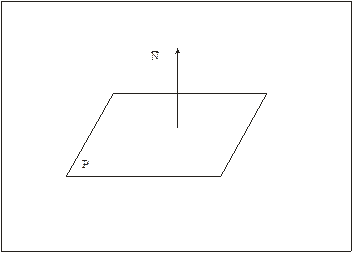
Рис. 3
Для плоскости 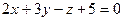 нормальным является вектор
нормальным является вектор 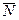 =
= 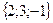 .
.
Отметим, что любой вектор, коллинеарный вектору 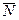 =
= 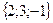 так же является нормальным вектором плоскости
так же является нормальным вектором плоскости 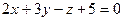 . Таким образом, при каждом ненулевом
. Таким образом, при каждом ненулевом 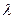 вектор с координатами
вектор с координатами 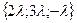 будет являться нормальным вектором рассматриваемой плоскости.
будет являться нормальным вектором рассматриваемой плоскости.
3) Найти косинус угла между плоскостями 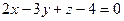 и
и 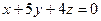 .
.
Решение.
Угол 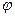 между двумя плоскостями
между двумя плоскостями 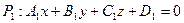 и
и 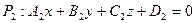 представляет собой угол между их нормальными векторами и определяется равенством
представляет собой угол между их нормальными векторами и определяется равенством
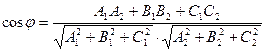
Для плоскости 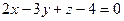 координаты нормального вектора
координаты нормального вектора 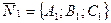 определяются равенствами
определяются равенствами 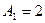 ,
, 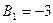 ,
, 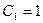 . Для плоскости
. Для плоскости 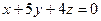 - равенствами
- равенствами 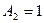 ,
, 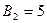 ,
, 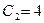 . Следовательно,
. Следовательно, 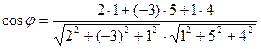 =
= 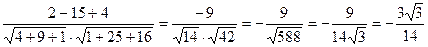 .
.
4) Составить уравнение плоскости 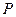 , проходящей через точку
, проходящей через точку 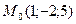 параллельно плоскости
параллельно плоскости 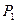 :
: 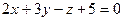 .
.
Решение.
Уравнение плоскости, проходящей через точку 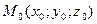 , имеет вид
, имеет вид
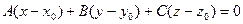 (3.8)
(3.8)
Подставим в уравнение (3.8) координаты точки 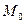 :
: 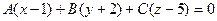 .
.
Условие параллельности плоскостей 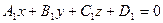 и
и 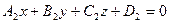 имеет вид
имеет вид
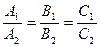 (3.9)
(3.9)
Так как плоскости 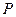 и
и 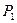 параллельны, то в качестве нормального вектора
параллельны, то в качестве нормального вектора 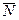 плоскости
плоскости 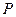 можно взять нормальный вектор
можно взять нормальный вектор 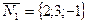 плоскости
плоскости 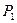 , т.е. в формуле (3.9) отношение
, т.е. в формуле (3.9) отношение 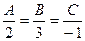 можно принять равным единице. Следовательно, уравнение плоскости
можно принять равным единице. Следовательно, уравнение плоскости 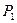 примет вид
примет вид 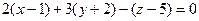 . Запишем это уравнение в общем виде:
. Запишем это уравнение в общем виде: 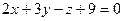 .
.
5) Найти расстояние от точки 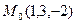 до плоскости
до плоскости 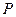 :
: 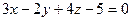 .
.
Решение.
Расстояние 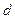 от точки
от точки 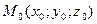 до плоскости
до плоскости 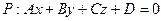 представляет собой длину перпендикуляра, опущенного из точки на плоскость, и определяется формулой
представляет собой длину перпендикуляра, опущенного из точки на плоскость, и определяется формулой
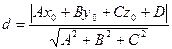 (3.10)
(3.10)
Для плоскости 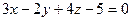 координаты нормального вектора
координаты нормального вектора 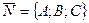 определяются равенствами
определяются равенствами 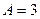 ,
, 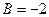 ,
, 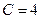 . Следовательно,
. Следовательно, 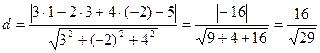 .
.
6) Составить канонические уравнения прямой, проходящей через точки 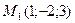 и
и 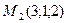 .
.
Решение.
Уравнения прямой, проходящей через точки 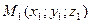 и
и 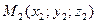 имеют вид
имеют вид
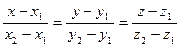 (3.11)
(3.11)
Так как 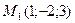 ,
, 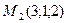 , то в силу (3.11) получим уравнения
, то в силу (3.11) получим уравнения 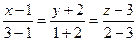 или
или 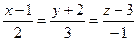 .
.
7) Найти направляющий вектор прямой 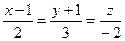 .
.
Решение.
Направляющий вектор 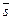 - это вектор, параллельный прямой.
- это вектор, параллельный прямой.
Если прямая задана каноническими уравнениями 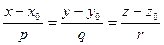 , то направляющий вектор
, то направляющий вектор 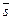 имеет координаты
имеет координаты 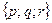 .
.
Рис. 4
Для рассматриваемой прямой 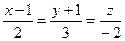 направляющим вектором является вектор
направляющим вектором является вектор 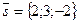 .
.
Отметим, что любой вектор, коллинеарный вектору 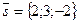 так же является направляющим вектором прямой
так же является направляющим вектором прямой 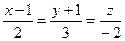 . Таким образом, при каждом ненулевом
. Таким образом, при каждом ненулевом 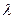 вектор с координатами
вектор с координатами 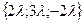 будет являться направляющим вектором рассматриваемой прямой.
будет являться направляющим вектором рассматриваемой прямой.
8) Найти косинус угла между прямыми 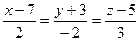 и
и 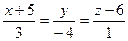 .
.
Решение.
Угол 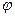 между двумя прямыми
между двумя прямыми 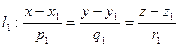 и
и 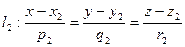 представляет собой угол между их направляющими векторами и определяется равенством
представляет собой угол между их направляющими векторами и определяется равенством
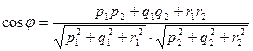
Для прямой 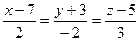 координаты направляющего вектора
координаты направляющего вектора 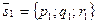 определяются равенствами
определяются равенствами 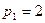 ,
, 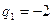 ,
, 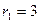 . Для прямой
. Для прямой 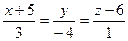 - равенствами
- равенствами  ,
, 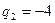 ,
, 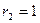 . Значит,
. Значит, 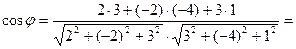
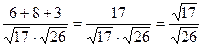 .
.
9) Составить канонические уравнения прямой 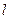 , проходящей через точку
, проходящей через точку 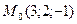 параллельно прямой
параллельно прямой 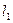 :
: 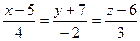 .
.
Решение.
Канонические уравнения прямой имеют вид 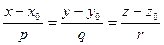 . Здесь
. Здесь 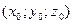 - координаты точки, через которую проходит прямая.
- координаты точки, через которую проходит прямая.
В канонические уравнения прямой 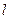 подставим координаты точки
подставим координаты точки 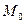 . Получим:
. Получим: 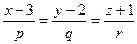 .
.
Условие параллельности прямых 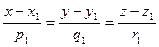 и
и 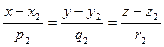 имеет вид
имеет вид
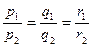 (3.12)
(3.12)
Так как прямые 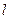 и
и 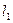 параллельны, то в качестве направляющего вектора
параллельны, то в качестве направляющего вектора 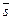 прямой
прямой 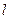 можно взять направляющий вектор
можно взять направляющий вектор 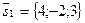 прямой
прямой 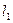 , т.е. в формуле (3.12) отношение
, т.е. в формуле (3.12) отношение 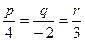 можно принять равным единице. Следовательно, уравнение прямой
можно принять равным единице. Следовательно, уравнение прямой 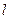 примет вид
примет вид 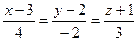 .
.
10) Найти угол между прямой 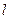 :
: 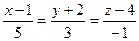 и плоскостью
и плоскостью 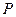 :
: 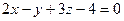 .
.
Решение.
Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость. Угол 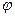 между прямой и плоскостью равен
между прямой и плоскостью равен 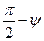 , где
, где 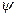 - угол между направляющим вектором
- угол между направляющим вектором 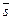 прямой и нормальным вектором
прямой и нормальным вектором 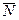 плоскости.
плоскости.
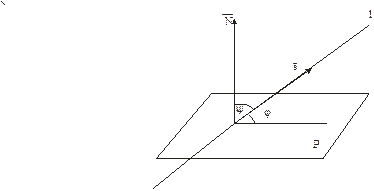
Рис. 5
Угол 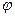 между прямой
между прямой 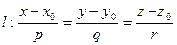 и плоскостью
и плоскостью 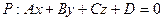 определяется формулой
определяется формулой
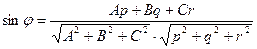
Для плоскости 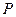 :
: 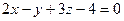 координаты нормального вектора
координаты нормального вектора 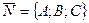 определяются равенствами
определяются равенствами 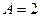 ,
, 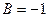 ,
, 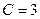 . Для прямой
. Для прямой 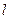 :
: 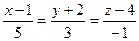 координаты направляющего вектора
координаты направляющего вектора 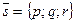 - равенствами
- равенствами 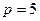 ,
, 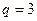 ,
, 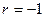 . Синус угла между прямой и плоскостью равен
. Синус угла между прямой и плоскостью равен 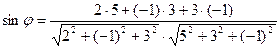 =
= 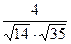
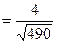 . Следовательно,
. Следовательно, 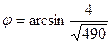 .
.
11) Составить уравнение плоскости 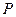 , проходящей через точку
, проходящей через точку 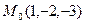 перпендикулярно прямой
перпендикулярно прямой 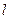 :
: 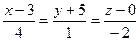 .
.
Решение.
Уравнение плоскости, проходящей через данную точку, имеет вид 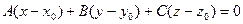 .
.
Подставим в указанное уравнение координаты точки 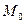 . Получим:
. Получим: 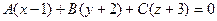 .
.
Условие перпендикулярности плоскости 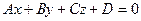 и прямой
и прямой 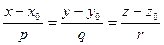 имеет вид
имеет вид
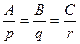 (3.13)
(3.13)
Так как искомая плоскость 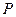 перпендикулярна прямой
перпендикулярна прямой 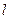 , то в качестве нормального вектора
, то в качестве нормального вектора 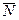 плоскости можно взять направляющий вектор
плоскости можно взять направляющий вектор 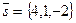 прямой
прямой 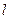 , т.е. в формуле (3.13) отношение
, т.е. в формуле (3.13) отношение 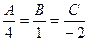 можно принять равным единице. Следовательно, уравнение плоскости
можно принять равным единице. Следовательно, уравнение плоскости 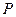 примет вид
примет вид 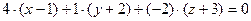 . Запишем это уравнение в общем виде:
. Запишем это уравнение в общем виде: 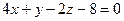 .
.
12) Составить канонические уравнения прямой 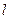 , проходящей через точку
, проходящей через точку 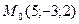 перпендикулярно плоскости
перпендикулярно плоскости 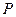 :
: 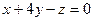 .
.
Решение.
Канонические уравнения прямой, проходящей через данную точку, имеют вид 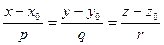 .
.
Подставим в эти уравнения координаты точки 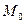 . Получим:
. Получим: 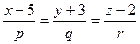
Условие перпендикулярности прямой 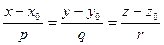 и плоскости
и плоскости 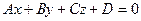 имеет вид
имеет вид 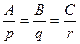 .
.
Так как прямая 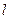 перпендикулярна плоскости
перпендикулярна плоскости 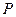 , то в качестве направляющего вектора
, то в качестве направляющего вектора 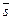 прямой
прямой 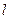 можно взять нормальный вектор
можно взять нормальный вектор 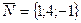 плоскости
плоскости 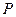 , т.е. в формуле (3.13) отношение
, т.е. в формуле (3.13) отношение 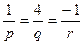 можно принять равным единице. Следовательно, уравнение прямой
можно принять равным единице. Следовательно, уравнение прямой 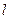 примет вид:
примет вид: 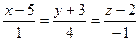 .
.
13) Найти координаты точки пересечения прямой 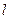 :
: 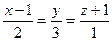 и плоскости
и плоскости 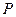 :
: 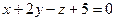 .
.
Решение.
Координаты точки 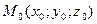 пересечения прямой
пересечения прямой 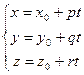 и плоскости
и плоскости 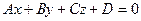 представляют собой решение системы
представляют собой решение системы
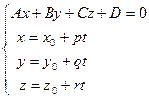 (3.14)
(3.14)
Запишем параметрические уравнения прямой 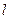 :
: 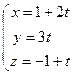 и подставим выражения для
и подставим выражения для 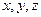 в уравнение плоскости
в уравнение плоскости 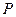 :
: 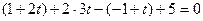 . Отсюда
. Отсюда 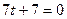 ;
; 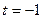 . Подставим найденное значение
. Подставим найденное значение 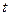 в параметрические уравнения прямой
в параметрические уравнения прямой 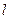 :
: 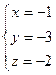 . Следовательно,
. Следовательно, 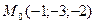 .
.
Задача №3.
К кривым второго порядка относятся эллипс (рис.6), гипербола (рис. 7 и 8), парабола (рис. 9-12). Приведем рисунки и канонические уравнения этих кривых.
Эллипс 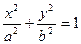
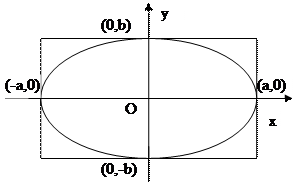
Рис. 6
Гипербола 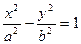 Гипербола
Гипербола 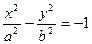 .
.
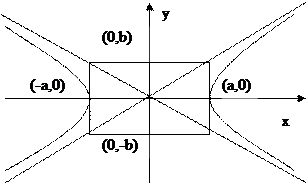
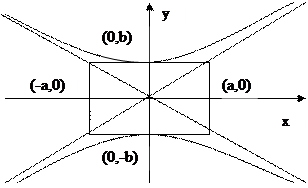
Рис. 7 Рис. 8
Парабола 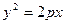 Парабола
Парабола 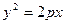
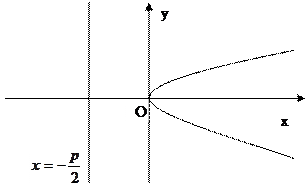
Рис. 9
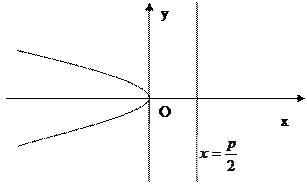
Рис. 10
Парабола 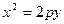 Парабола
Парабола 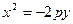
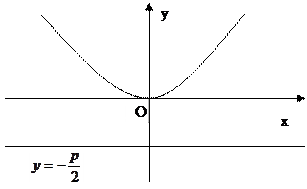
Рис. 11
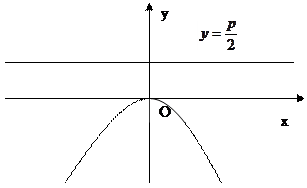
Рис. 12
Приведем примеры решения задачи №3.
Пример 1. Привести уравнение кривой второго порядка 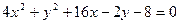 к каноническому виду и построить кривую.
к каноническому виду и построить кривую.
Решение.
Для приведения уравнения кривой второго порядка к каноническому виду применяют метод выделения полного квадрата.
Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при 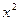 и
и 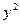 вынесем за скобки:
вынесем за скобки: 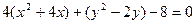 .
.
Выделим полный квадрат: 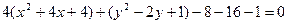 . Отсюда
. Отсюда 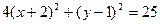 . Разделим обе части равенства на 25:
. Разделим обе части равенства на 25: 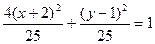 . Запишем полученное уравнение в каноническом виде:
. Запишем полученное уравнение в каноническом виде: 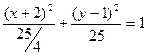 .
.
Выполним параллельный перенос осей координат по формулам 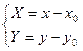 . При таком преобразовании начало координат переносится в точку
. При таком преобразовании начало координат переносится в точку 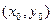 , уравнение эллипса принимает канонический вид
, уравнение эллипса принимает канонический вид 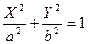 .
.
В нашем примере 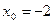 ,
, 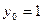 ,
, 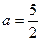 ,
, 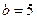 .
.
Итак, рассматриваемое уравнение определяет эллипс с центром в точке 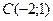 и полуосями
и полуосями 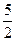 и
и 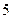 .
.
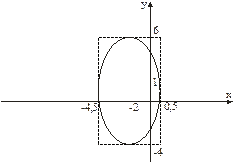
Рис. 13
Пример 2. Привести уравнение кривой второго порядка 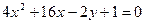 к каноническому виду и построить кривую.
к каноническому виду и построить кривую.
Решение.
Как и в предыдущем примере, сгруппируем слагаемые, содержащие текущие координаты: 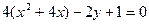 .
.
В скобках выделим полный квадрат: 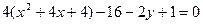 ;
; 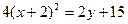 . Отсюда
. Отсюда 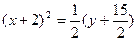 .
.
Выполним замену переменных 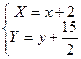 . После этого преобразования уравнение параболы принимает канонический вид
. После этого преобразования уравнение параболы принимает канонический вид 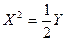 , вершина параболы в системе координат
, вершина параболы в системе координат 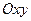 расположена в точке
расположена в точке 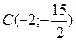 .
.
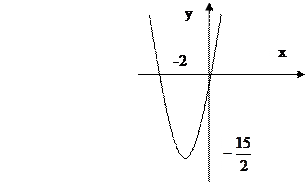
Рис. 14
Задача №4.
Кривая задана в полярной системе координат уравнением 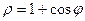 .
.
Требуется:
1) найти точки, лежащие на кривой, давая 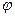 значения через промежуток, равный
значения через промежуток, равный 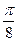 , начиная от
, начиная от 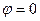 до
до 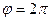 ;
;
2) построить полученные точки;
3) построить кривую, соединив построенные точки (от руки или с помощью лекала);
4) составить уравнение этой кривой в прямоугольной декартовой системе координат.
Решение.
Сначала построим таблицу значений 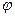 и
и 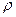 :
:
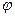
| 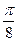
| 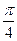
| 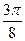
| 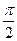
| 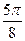
| 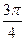
| 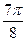
| 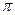
| 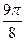
| 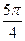
| 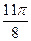
| 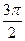
| 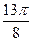
| 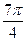
| 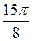
| |
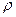
| 2,00 | 1,92 | 1,71 | 1,38 | 1,00 | 0,62 | 0,29 | 0,08 | 0,00 | 0,08 | 0,29 | 0,62 | 1,00 | 1,38 | 1,71 | 1,92 |
Построим эти точки в полярной системе координат. Полярная система координат состоит из начала координат 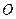 (полюса) и полярной оси
(полюса) и полярной оси 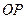 . Координаты точки
. Координаты точки 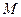 в полярной системе координат определяются расстоянием
в полярной системе координат определяются расстоянием 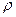 от полюса (полярным радиусом) и углом
от полюса (полярным радиусом) и углом 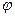 между направлением полярной оси и полярным радиусом (полярным углом). Для того, чтобы построить точку
между направлением полярной оси и полярным радиусом (полярным углом). Для того, чтобы построить точку 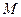 , необходимо построить луч, выходящий из точки
, необходимо построить луч, выходящий из точки 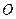 под углом
под углом 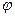 к полярной оси; отложить на этом луче отрезок длиной
к полярной оси; отложить на этом луче отрезок длиной 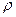 .
.
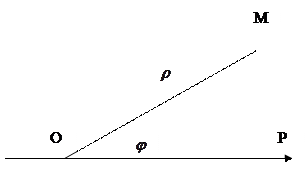
Рис. 15
Построим все точки, определенные в таблице и соединим их плавной линией
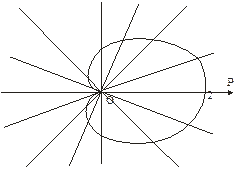
Рис. 16
Запишем уравнение рассматриваемой кривой в прямоугольной декартовой системе координат. Для этого воспользуемся формулами перехода от декартовой к полярной системе координат.
Если полюс совпадает с началом координат прямоугольной декартовой системы координат, полярная ось – с осью абсцисс, то между прямоугольными декартовыми координатами 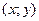 и полярными координатами
и полярными координатами 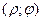 существует следующая связь:
существует следующая связь:
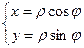 ,
, 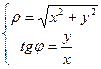
Откуда
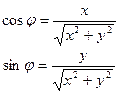
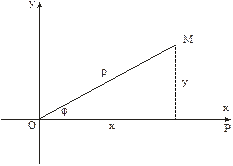
Рис. 17
Итак, в уравнении исходной кривой 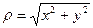 ,
, 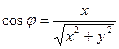 . Поэтому уравнение
. Поэтому уравнение 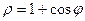 принимает вид
принимает вид 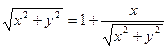 . После преобразований получим уравнение
. После преобразований получим уравнение 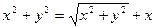 .
.
Задача №5.
Построить на плоскости геометрическое место точек, определяемое неравенствами
1) 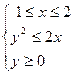
2) 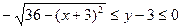
Решение.
Для того, чтобы решить неравенство 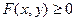 на плоскости, надо построить график линии
на плоскости, надо построить график линии 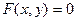 . Кривая
. Кривая 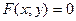 разбивает плоскость на части, в каждой из которых выражение
разбивает плоскость на части, в каждой из которых выражение 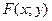 сохраняет свой знак. Выбирая пробную точку в каждой из этих частей, найдем часть плоскости, являющуюся искомым решением неравенства.
сохраняет свой знак. Выбирая пробную точку в каждой из этих частей, найдем часть плоскости, являющуюся искомым решением неравенства.
1) Построим прямые 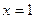 и
и 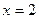 , заштрихуем область, в которой
, заштрихуем область, в которой 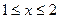 . Затем построим параболу
. Затем построим параболу 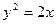 и заштрихуем область, содержащую ось симметрии параболы (расположенную внутри параболы); построим прямую
и заштрихуем область, содержащую ось симметрии параболы (расположенную внутри параболы); построим прямую 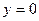 и заштрихуем область, лежащую выше прямой. Пересечение всех заштрихованных областей и определит множество точек, представляющих решение рассматриваемой системы.
и заштрихуем область, лежащую выше прямой. Пересечение всех заштрихованных областей и определит множество точек, представляющих решение рассматриваемой системы.
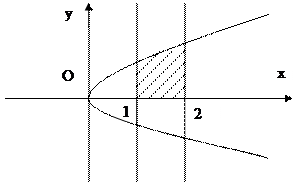
Рис. 18
2) Построим линию, определяемую уравнением 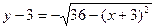 . Эта линия представляет собой ту часть окружности
. Эта линия представляет собой ту часть окружности 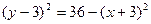 или
или 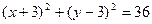 , на которой
, на которой 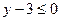 . Далее построим прямую
. Далее построим прямую 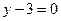 (
(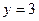 ). Решением рассматриваемого двойного неравенства является часть плоскости, расположенная между нижней половиной окружности
). Решением рассматриваемого двойного неравенства является часть плоскости, расположенная между нижней половиной окружности 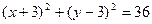 с центром в точке
с центром в точке 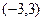 радиуса
радиуса 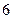 прямой
прямой 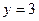 .
.
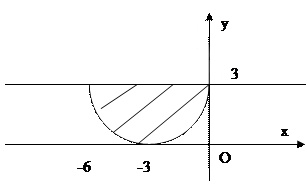
Рис. 19
Контрольная работа
Вариант 1.
Задача 1. Даны три последовательные вершины параллелограмма А(1;2), В(-1;3),С(-4;-2). Не находя координаты вершины D, найти:
6) уравнение стороны AD;
7) уравнение высоты BK, опущенной из вершины В на сторону AD;
8) длину высоты BK;
9) уравнение диагонали BD;
10) тангенс угла между диагоналями параллелограмма.
Записать общие уравнения найденных прямых. Построить чертеж.
Задача 2. Даны точки A(1;2;3), B(-1;3;5), C(2;0;4), D(3;-1;2). Найти:
1) общее уравнение плоскости АВС;
2) общее уравнение плоскости, проходящей через точку D параллельно плоскости АВС;
3) расстояние от точки D до плоскости ABC;
4) канонические уравнения прямой АВ;
5) канонические уравнения прямой, проходящей через точку D параллельно прямой AB;
6) общее уравнение плоскости, проходящей через точку D перпендикулярно прямой AB.
Задача 3. Уравнение второго порядка 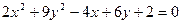 путем выделения полного квадрата привести к каноническому виду. Построить кривую, определяемую этим уравнением.
путем выделения полного квадрата привести к каноническому виду. Построить кривую, определяемую этим уравнением.
Задача 4. Кривая задана в полярной системе координат уравнением 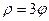 .
.
Требуется:
5) найти точки, лежащие на кривой, давая 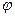 значения через промежуток, равный
значения через промежуток, равный 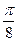 , начиная от
, начиная от 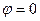 до
до 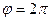 ;
;
6) построить полученные точки;
7) построить кривую, соединив построенные точки (от руки или с помощью лекала);
8) составить уравнение этой кривой в прямоугольной декартовой системе координат.
Задача 5. Построить на плоскости геометрическое место точек, определяемое неравенствами
1) 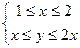 ;
;
2) 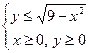
Дата публикования: 2015-11-01; Прочитано: 2755 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
