 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Геометрия зацепления цилиндрической червячной передачи
|
|
Основными геометрическими параметрами червяка являются (рис. 9.4):
· диаметр начального цилиндра dw 1;
· диаметр делительного цилиндра d 1 (если червячное зацепление выполнено без смещения режущего инструмента совпадает с начальным);
· диаметр цилиндра выступов dа 1;
· диаметр цилиндра впадин df 1;
· длина нарезанной части червяка b 1;

da 2
 | |||
 | |||
02
 n db 2
n db 2
 | |||
 | |||
an
df 2 N aw
P
da 1 d 1 df 1
B1 n

Рис. 9.4
Наиболее часто встречаются червяки у которых сечение винта трапецеидальное с углом при вершине 40°. В плоскости перпендикулярной оси колеса червячное зацепление представляет собой эвольвентное реечное зацепление, поэтому геометрические размеры зубьев червяка и червячного колеса совпадают с размерами зубьев цилиндрического прямозубого колеса. Единственное отличие, то, что величина радиального зазора равна 0,2× m.
Поверхность червяка представляет собой совокупность винтовых линий. В зависимости от направления винтовой линии различают правые и левые винтовые поверхности червяков. Перемещая винтовую линию вдоль образующей цилиндра на некоторую долю шага, получаем параллельно расположенную винтовую линию, которую называют заходом. Червяки бывают одно-, двух-, трех- и четырёх- заходные. Число заходов удобнее определять по торцевому сечению (рис. 9.5) и обозначают Z 1.

Рис. 9.5
Установим связь между диаметром делительного цилиндра и числом заходов червяка. Так как червяк представляет собой винт, то его развертка захода представляет собой наклонную линию под углом l (угол подъема винтовой линии) (рис. 9.6).

 d 1 S = p×Z 1
d 1 S = p×Z 1



 S
S

l l
 |  |


 p× d 1
p× d 1

Рис. 9.6
 ,®
,®  ,
,
где S – ход червяка, это путь который проходит точка делительного цилиндра за время одного оборота червяка:
 ,
,
здесь р – шаг нарезки червяка.
Отсюда:
 ®
®  .
.
В целях создания определенной номенклатуры инструмента, применяемого для изготовления червяков (червячных фрез) в полученную формулу вводится коэффициент червяка  , тогда:
, тогда:
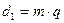 .
.
Наряду с осевым шагом у многозаходных червяков различают и торцевой шаг pt равный длине дуги окружности делительного цилиндра между двумя соседними заходами, исходя из рис. 9.6 получаем:
 .
.
Дата публикования: 2015-11-01; Прочитано: 458 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
