	Главная \| Случайная страница \| Контакты \| Мы поможем в написании вашей работы!

2 страница. Бұл процедураның стандарттық жүзеге асырылудан айырмашылығы бар

⇐ Предыдущая 123 4 5 Следующая ⇒

for i:=2 to m do

if a[i]≤r then a[i-1]:=a[i]

Else

begin a[i-1]:=r; r:=a[i]; end;

a[m]:=r;

End

Бұл процедураның стандарттық жүзеге асырылудан айырмашылығы бар.

«Көпіршіктік сұрыптау»,сондай-ақ барлық басқа да сұрыптау алгоритмдерінде массив элемент/інің алмасу саны бастапқы массивтің элемент/ң орналасуын тәуелді болып келеді. Яғни, жалпы алғанда n элементтен құрылған массивте ауысу саны n!.

Массивтерді реттеу есептерінде түйінді рольді үшін төменгі бағанның бірі атқарды, дәлірек айтқанда . Ал салыстыру саны алмастыру санымен мынандай қарапайым теңсіздікпен байланысты 2^l , мұндағы l салыстыру саны. Мұнда біз массив элементерінің алғашқы орналасуының жаман варианттарына көңілімізді көбірек бөлеміз. Яғни алгоритмның жұмысының қортындысында алмастыру немесе салыстыру саны максимум болатын варианттарды қарастырамыз. Осыған қоса іздеу және сұрыптау алгоритмнің эффективтігінен бағалауда маңызды орын алатын эффективтіліктің «орташа» бағасы болады, яғни барлық алмастырулар бойынша алынған орташа бағасы.

Айтылған сұрыптау алгоритмін тиімділеу үшін бірнеше жол/ бар. Мысалы, алгоритм n элементі массивті реттеуде n-1 итерация қажет етеді. Бірақ массивтің элемент/іне байланысты, алгоритм оны n-1 итерациядан кем итерациядан реттеуі мүмкін. Осыны ескерсек, онда ондай жағдайларда тексеруді ұйымдастыруға болады. Әр итерацияда кем дегенде бір рет алмасу жүргізілсе, онда true (ақиқат) мәнін қабылдайтын қосымша логикалық айнымалы енгізуге болар еді. Сонымен қатар, әр жаңа итерацияның алдында бұл айнымалының мәнін қосымша тексеріп отыру қажет.

Көпіршіктеу сұрыптау алгоритмінің тиімділігін арттыру үшін процедураны келесі түрде ұйымдастыруды ұсынуға болады:әрбір келесі тізбектік айналу кезекпен және қарама-қарсы бағытта жүргізілсе.Сондай-ақ,егер аппараттық сүйемелдеу болса,онда бастапқы тізбектік есептеу процесін «конвейерлеп» отырып k көпіршіктерді бірінен кейін бірін жіберудің мәні бар.

15. Бинарлы ағаштармен жасалатын стандарты операциялар

Ағаш/ды телу арнайы операция/ын пайдаланып, қайталанба айналым/ң тиімді екендігін көрсететін жолмен жүруімізге б-ды. М/ы, ағаштың симметриялы айналымында ағашты оң жақтан симметриялы телінген ағаш түрінде құруға б-ды.

Штрихтелінген бағыттауыш жіп д.а ж/е ол кері бағытты қозғалыс кезінде, симметриялы айналымда келесі кезекте болып өтетін түпкі ағашты көрсетеді.

Енді симметриялы телінген ағашта, симметриялы айналуда алдыңғы сәйкес төбеге бір қосымша ұяшықты бағыттаушы жіп ретінде қосып, стекті пайдаланбай-ақ, іске асыруға болады.

Тура ретпен орналасқан айналымдар үшін оң жақтан тура (түзу) телінген ағаштарды қосуға болады. Бағыттауыштар бұл ағашта түпкі ағашты емес, енді тура ретті айналымдағы келесі кезекте болатын төбені көрсетеді. Сондай-ақ, кері реттегі айналымға да қатысты. Енді жоғарыда көрсетілген екі суретте де бағыттың айырмашылығын анықтау пайдалы болады. Сонымен қатар, мұнда ағаштардың сол жақтан симметриялы және сол жақтан тура телінген класстарын еске сақтаған жөн. Сол жақтан симметриялы телінген ағаш жағдайында, әрбір сол жақтағы бағыттауыш ағаштың сәйкес төбесіндегі симметриялы ретте жүргізілетін, берілген түйіннің алдыңғысына сілтеме жібі болады. Тура осылай,сол жақтан тура телінген ағаш үшін ағаштың сәйкес төбесінде әрбір сол жақтағы бағыттауыштың, ағаштың тура бағытындағы өзінің алдыңғысына сілтеме жібі болады.

Бинарлы ағаш/ға жүргізілетін операция/. Жаңа операция/ тізімін микрооперация/дан бастауға болады, олардың ішінен келесі операция/ды ерекшелейік:

· copy(t,v’)- Бұл функция t-ағашының көшірмесінің түбірі – V’-түйініне көрсеткішті қайтарады.

· ecv(t1,t2) – аргументтері екі бинарлы ағаш болатын, ал нәтижесі, егер эквиваленттілік орындалса true мәнін, кері жағдайда false мәнін қабылдайтын эквиваленттілік операциясы.

· subtree(v,t) – операциясы түбірі t- ағашының қандай да бір V- төбесі болатын, t- ағашының ішкі ағашын қайтарады. Дәлірек айтсақ, subtree операциясы сілтемені v- түйініне қайтарады.

Енді келесі операцияларды қарастырсақ:

· inf(v,t’) функциясы t- ағашының v- түйінінің құрамын толығымен қайтарады.

· right_des (v,t’) left_dess (v,t) функция/ы t- ағашының v-төбесінің сәйкес тікелей оң және сол жақ ұрпақтарына көрсеткіштерді қайтарады, әрине егер олар бар болса.

· anc(V,t) функциясы t-ағашында V-төбесінің тікелей тегіне көрсеткішті қайтарады, егер олар табылса.

· change (V,V’,t) t- ағашындағы V- түйінімен V’ түйінін ауыстырады (алмастырады).Бұл операция макрооперацияға қарағанда дербес болып табылады.

Маңызды және сондай-ақ бастапқы операция болып табылатын make tree (V,V’, V”, t) операциясы t- ағашын V’ түйініндегі түбірмен және V’ түйінінен шығатын V’-сол және V’-оң жақ ішкі ағаштар түбірлеріне бағыттаушылармен береді.

Бинарлы ағаштарға жиі қолданылатын операция болып ins(V,t) операциясы табылады, ол t- ағашына жаңа V түйінін кірістіру операциясы.

16. Толықтау бинарлы ағашт және оның ерекшеліктері

Бинарлы ағаштың өсу нүктесі деп вакантты бағыт бойынша жаңа қабырға тұрғызуға болатын төбені айтады.

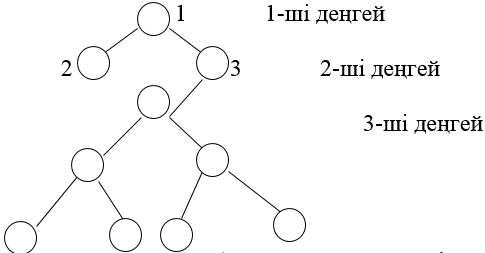
Егер бинарлы ағаштың барлық өсу нүкте/і соңғы деңгейде орналасса, онда ол толық д.а. Толық ағаштың ақырғы/ынан өзге әрбір төбесі 2 тікелей ұрпаққа ие болады, ал түбірден басталатын ж/е ақырғы төбеде аяқталатын барлық жол/дың ұзындығы бірдей болады ж/е бұл кезде мұндай жолдағы әрбір қабырға бір ғана рет өтіледі.

Толық бинарлы ағаштың k деңгійіндегі төбелердің саны n мынаған те болады

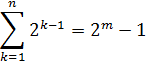
Толық ағаштағы элемент іздеу жылдам орындалады, ең көп дегенде log₂ n слыстыру жасалады, бірақ бастапқы массивте «екінің дәрежесі минус бір» тең элементтер саны болады деген үміт үлкен емес. Осыған байланысты толықтау ағаш түсінігін қарастырайық, бұл типті ағашты теңестірілген дейді және оны элементтер саны еркін алынатын масссив үшін тұрғызуға қолдануға болады.

Бинарлы ағашты толықтау дейміз, егер оның барлық өсу нүктелері осы ағаштың тек соңғы және соңғының алдындағы деңгейлерде орналасса.

Кейде мұндай ағашты толықтау баланстандырылған деп те атайды.

Егер толықтау ағашта m деңгейінен жоғары төбелер жоқ десек, онда элементті іздеуге қажетті салыстырулардың максималды саны былай бағаланады:

log₂ n < m≤ log₂ n+1

яғни, толықтау ағаш үшін іздеу есебі оптималды- минималды уақытта шешіледі, яғни салыстыру саны минималды болады. Толықтау ағашш тұрғызу алгоритмі күрделі емес, бірақ бұл ағаштардың айтарлықтай кемшіліктері бар. Егер массив статикалы болса, яғни, элементтер саны да, элементтің өзі де өзгермесе, онда толықтау ағашты іздеуге қолдану негізді болып табылады. Мұндай ағашты ұйымдастыруға бір рет уақыт жұмсаса, ары қарай тек іздеу есебі ғана жүргізіледі және ол тиімді болады. егер массивтің элемент/і периодты түрде өзгерсе н/е қосылса н/е алынатын болса, онда бұл басқа бір мәселе.

Дәстүрлі түрде 6 элементтен тұратын массивті жне оның толықтау ағашын қарастырайық:

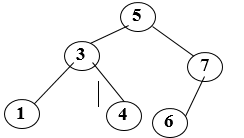
Бір ғана «2» элементін қосу ағашты қайта құруды керек етедіғ бұл кезде массивтің тек бір элементі ғана өз орнында қалады.

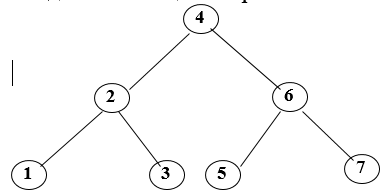
Бастапқы массив бойынша толықтау ағаш тұрғызу алгоритмі қарапайым болғанымен, бұл типті ағаштарды динамикалық массивтерге қолдану тиімділігі өте төмен болады. себебі жоғарыда көргеніміздей массив аз ғана өзгеріске түскен кезде ағашты айтарлықтай немесе толық қайта құру қажет болады.

17. Ақпараттық іздеу түсінігі

Іздеу әдістері және іздеумен байланысты есептерді зерттеу мәселесі, зерттеулердің жеке және қызықты бағыттарының бірі [5,16]. Іздеу есебімен, сұрыптаумен және деректер құрылымымен байланысты барлық тақырыптарды осы кітапшада толық қарастыруға мүмкін емес екендігі анық.

Іздеу алгоритмін әдісін жақсарту арқылы салыстыру санының бағасын жақсартуға болады. Компьютерлің жүйелерде көп тараған екілік іздеу алгоритмінің салыстыру санының күрделілігінің жоғарыдан бағасы log₂n жуық. Салыстырмалы түрде салыстыру санының алгоритмдегі күрделілігінің бағалары n-нің үлкен мәнінде өте жақсы байқалады.

Әр түрлі әдебиеттерде және қолданбаларда екілік немесе бинарлы іздеу алгоритмнің нұсқаларының бір бірінен үлкен айырмашылықтары жоқ, барлық процедуралар бір есептеу схемасын қамтамасыз етеді. Дәлдеп айтсақ, реттелген бастапқы массивті қақ екіге бөліп, орташа элементін берілген р* мәнімен салыстыра отырып, массивтің қай бөлігінде ізделінетін элемент орналасқанын анықтайды. Келесі қадамда анықталған массивтің бөлігін қайтадан екіге бөліп, орташасын р* салыстырады және тағы сол сияқты. Осылай массивті қақ бөлу арқылы р* мәніне тең элемент және оның реттік нөмірі табылады немесе ондай мәнге тең элемент жоқ екені анықталады.

Сонымен, қарапайым ақпараттарды іздеу есебінде белгілер массивінің p1, p2, …, pn элементтері ретіндесандар орнында бекітілген алфавиттің сөздері мен әріптері де болуы мүмкін. Ең белгілі мысал телефондық кәтапшадан іздеу мысалы болып табылады. Кітапшадан фамилиясы арқылы телефон нөмірін анықтау немесе кем дегенде абоненттің фамилиясы жазылған кітапша бетінің нөмірін табу. Мұндай эффективті алгоритмді массивті реттеу алгоритмінде де қолдануға болады.

18. O(n log₂n) күрделілігімен сұрыптаудың ерекшеліктері

Cұраптаудың тиімділігі жад пен уақыт тұрғысынан бағаланады. Егерде нақты сұрыптау алгоритмінің тиімділігі жайлы айтсақ, онда салыстырулар саны қарастырылады. Элементтерді салыстыру негізінде ең танымал сұрыптау алгоритм/і - O(n2) күрделілігі сұрыптау, ал ең тиімді/і O(n log2 n) күрделілігін талап етеді.

Қарастырылатын алгоритм таңдаумен сұрыптау алгоритмдері классына жатады. Бірақ бұл алгоритмнің өзінің ерекше қасиеттері бар. Біріншіден, бастапқы массив бинарлы ағашпен беріледі. Бұл бинарлы ағаш құрылысы жағынан ерекшеленіп келеді, ондай ағаштарды толықтау бинарлы ағаштар деп атайды. Реттеу процессі екі этаптан тұрады. Бірінші этапта пирамида тәріздес ағаш түзіледі. Екінші этапта құрылған ағаш пирамидасында түйіндеріне бекітілген массив элементтері түпкілікті реттеуге пайдаланылады. Бұл этапта пирамиданың элементтерін реттеу бағыты пирамиданың оң жағынан солға қарай, төменнен жоғарыға қарай қажет болған жағдайда алмастырылады. Екінші этап бірнеше фазадан тұрады. 1-фазада массивтің реттелмеген бөлігіндегі ағымдық максималды элемент пирамиданың төменгі оң бұрышында орналасқан элементпен алмастырылады. Сөйтіп, ағымдық максималды элемент реттелген массивте өзінің орнын табады. Осыдан кейін бұл максималды элемент те, оның орны да реттеуде қарастырылмайды. 2-этаптың 1-фазасының нәтижесінде пирамиданың құрылысы қайтадан құрылады.

HeapSort алгоритмінің тағы бір ерекшелігі алгоритмнің күрделілігі өзгермейтіндігінде. Жаман жағдайда н/е орташа алғанда да күрделілігі 0(n log2n) тең. Жоғарыдан бағасы орташаға жақын екенін дәлелдеуге болады. Бірақ дәл бағасын есептеу күрделі нәрсе. Екінші қызықты ерекшелігі бұл сұрыптауды жүргізуге қажетті қосымша жадтың минималдығында.

Стек. Алдын ала ескерсек, стек деректер құрылымы, кейбір жағдайлар магазин, динамикалық жадыны деп аталады. Осындай стек алдында тізбектеліп орналасқан шексіз «стек басы» және «түбі» ерекше ажыратылады. Процестің кезкелген уақыт мезетінде тек басына ғана оқу н/е жазу мүмкін болады. Осыған орай процесс барысында не өсіп не кеміп отырады. Еске салсақ, стек реттелген ұяшықтардан құрал5ан жады. Егер стек тізім ретінде ұйымдастырылса да, оны тізбектелген тізім ретінде көрсету жеңіл болып келеді.

Стек арқылы постфикстік түрдегі арифметикалық өрнекті есептеу алгоритмі қарапайым болып келеді.

Егер өрнектің кезекті символы операнд болса, онда оны стек басына келтіреміз.

Егер өрнектің келесі символы операция болса, онда стек басына келтіреміз. Операция операндылары осы уақыт мезетіне дейін стек операция белгісі орналасқан «этаждан» төмен «этаждарға» орналасады. Келесі қадамда операцияны орындап, орындалған операцияны және операндтарды стектен өшіреміз. Алынған нәтижені ең төменгі операндтар орналасқан «этажға» енгіземіз.

Өрнекте символдардың аяғына жеткенде есептеу тоқталады.

Quick Sort сұрыптауы. Quick Sort алгоритмінің күрделілігі орташалап алғанда 0(n log2n) жақын болады. Бастапқы берілген массивтің қандай да бір элементі таңдалып бекітіледі, әдетте массивтің ортаңғы н/е шеткі элемент/ін таңдайды ж/е тіректік элемент д.а. Қалған массив элемент/ін осы тіректік элем-тпен кезекпен салыстырады. Салыстыру нәт-де кезекті элемент тіректік элементтен үлкен болса, онда оны тіректік элементтің оң жағына орналастырады. Кері жағдайда сол жағына алмасады. Осы тіректік элем-т массивтің қалған барлық элемент/імен салыстырылғаннан кейін өзінің массивтегі түпкілікті орнын анықтайды. Сөйтіп, бұл элем-т жаңа массивтегі орнына жайғасып массивті 2ге бөледі.

19. Бинарлы ағаштар және оның қолдануы

Циклы жоқ, түбір деп аталатын ерекшеленген төбесі бар ақырлы байланысқан граф ағашы деп аталады.

Ағаш түбірімен қабырға арқылы байланысқан төбе оның тікелей ұрпағы болып табылады және бұл төбе мен сәйкес қабырға туралы олар түбірден бастау алады деп атайды. Әрбір мұндай төбе, егер ол соңғы болмаса, өзінің тікелей ұрпақтарына ие болады және т.с.с.. Бұл кезде ағаштың кез-келген төбесінің тікелей ұрпақтары туралы олар осы төбеден бастау алады деп атайды. Осындай төбелерді тікелей ұрпақтарымен қосатын қабырғалар туралы да айтуға болады. Мұнда ескере кететініміз ағаштың ақырғы төбелерінде ғана тікелей ұрпақ болмайды, бұл төбелер туралы әдебиеттерде басқа да атау бар – тығырықты немесе ілінген төбелер д.а.

Көбіне ағашты кеңістікте тұрғызғанда, мысалы жазықтықта ағаш төбелерін деңгейлері бойынша орналастырады немесе ярус бойымен. Ағаш түбірі 0 (немесе 1) деңгейінде орналасады, ары қарай түбірдің тікелей ұрпақтары келесі деңгейде орналасады және т.с.с.. Нәтижесінде ағаштың бірдей деңгейінің төбелері бір горизонталь бойына орналасады. Ең төменгі деңгейге ақырғы төбелердің кейбірі орналасады, ал қалған ақырғы төбелер ағаштың түрлі деңгейлері бойынша таралып орналасады. Егер мұндай ағашты өз центріне, яғни түбіріне қатысты 45 градусқа бұратын болса, онда мұндай түрлендіру нәтижесінде алынған фигура – сол бұрынғы ағаш, алайда оның бір деңгейдегі төбелері бір түзу бойымен орналасады, бірақ олар әр түрлі горизонтальда орналасады.

Сонымен, бинарлы ағаш деп әрбір төбесінен, түбірді қоса алғанда, екіден артық болмайтын қабырға шығатын ағашты айтады. Бұл кездегі бинарлы ағаштың әрбір төбесіне кіретін қабырға бірден аспайды.

Деңгейлерді сақтау ағаштармен орындалатын стандартты операцияның бірі – ағашты айналу кезінде көмегін тигізеді. Ағашты айналу кезінде оның барлық түйіндерін бір реттен ғана өтіп шығу қажет. Айналудың үш негізгі типі бар: тура, симметриялы және кері ретпен.

Бинарлы ағаш тәрізді құрылыс/конструкция/ практикалық жүйелерде қолданылғанымен, бинарлы ағаштардың Computer science аймағының өзінің ішінде қолданылуының көбірек маңызы бар. Бинарлы ағаштың қолданылуының бір түрімен оның айналымдарын анықтау кезінде таныстық, онда бинарлы ағаш арифметикалық өрнектерді көрсету үшін қолданылады.

Бинарлы ағаштың қолданылуының классикалық және анағұрлым көбірек айтылатын түріне минималды артықшылықтың Хаффман-код аталатын кодын құру үшін қолданылатын бинарлы ағаш жатады. Бинарлы ағаштардың шектелген – детерминдалған функцияларды беруде қолданылу мысалдары белгілі, мұндай функция/ туралы ғылымда бұл ағаштар арнайы атөа ие болады – нөмірленген ағаш/.

Бинарлы ағаштың қолданылуының мысал/н тақырыпта айтылған бөлім үшін де көрсетуге болады. Мұнда бинарлы ағаш/ мысалы, іздеу алгоритм/і мен массив/ді сұрыптау алгоритм/і үшін салыстыру сан/н төменгі бағалауды дәлелдеуде қолданылады.

Бинарлы ағаш/ң машиналық графикада. М/ы, жазықтықта іздеу есебін шешу үшін ж/е бақылау нүктесінің орнын ауыстыру кезінде статикалық сахнаның үшбұрыш/ң көрінісінің реттілігін анықтау есебін шешу үшін қолданылады.

20. Бинарлы ағашта кесте құру және оның ерекшеліктері

Идентификатор кестесінде элементті іздеу арқылы уақыт қысқартуға болады, белгілі уақытты үлкетпей-ақ, оны толтыру керек болады. Ол үшін кесте ұйымдастырудан үзіліссіз массив туріндег ұймдастырудан бас тарту керек.

Кестені құру әдісі бар. Кесте бинарлық ағаш формасын көрсетеді.

Әрбір ағаш тетігі кесте элементін көрсетеді. Бірақ түбірі бірінші элемент болып табылады. Қарсы компиляторды күту кезіндегі кесте толтыру керек. Себебі жоғарғы бөлігі екі бұтақтан көп болады. Екі бұтақты айыру үшін сол және оң деп атаймыз.

Бинарлық ағаш алгоритмін толтыруды қарайық. Алгоритм кіру бағыты бойынша жұмыс істейді делік, яғни, бойында идентификатор бар. Бірінші идентификаторды ағаштың басына орналастырамыз. Қалған идентификаторлар ағаштың басына келесідей орналастырамыз.

1. Идентификатордың кіру кезін таңдау. Егер идентификатор жоқ болса, онда ағашты құру бітті деп есептеуге болады.

2. Ағаш тетігін жоғарғы түбір ретінде алу

3. Идентификатордың атын басқа ағашында тетігі бар мен салыстыру

4. Егер идентификатор аз болса онда келесі 5-қадамға бару керек.

5. Егер тетіктің сол жағы бар болса онда оны орнында қалдырып 3-қадамғы қайту керек болмаса 6-қадамға бару керек.

6. Кері жоғарлықты жасау керек. Оның ішіне идентификатор жайлы мәліметтер салу керек және оны жаңа жоғарлықтың сол жағыны орналастыру қажет. Сосын кері 1-қадамға оралу

7. Егер тетіктің оң жағы болса,оны кері орнына әкеліп 3 –қадамға оралу керек.немесе 8 –қадамға бару керек.

8. Жаңа жоғарлықты жасау керек. Оның ішіне идентификатор жайлы мәліметтерді салу қажет. Осыны оң жақ қылып жасап 1-қадамға кері оралу қажет.

Ағаштағы элементті іздеу ағашты толтыру алгоритмі секілді болады:

1) Ағымдық түйіншек ретінде ағаштың түбірлік шыңы.

2) Ағымдық ағаш туйіншегінде бар ізделетін идентификатор атайымен идентификатор атауын салыстыру

3) Егер атаулар сәйкес келсе ізделініп жатқан идентификатор табылады, алгоритм тоқтайды алайда 4 қадамға өту керек.

4) Егер келесә идентификатор атауы кіші болса 5-ші қадамға өтуге болады, әйтпесе 6-шы қадамға.

5) Егер ағымдық түйіншекте сол жақ шыңы болса, онда оны ағымдық түйіншік ретінде алып 2-ші қадамға қайтамыз, әйтпесе ізделінетін идентификатор табылмай алгоритм жалғаспайды.

6) Егер ағымдық түйіншекте оң жақ шыңы болса, онда оны ағымдық түйіншік ретінде алып 2-ші қадамға қайтамыз, әйтпесе ізделінетін идентификатор табылмай алгоритм жалғаспайды.

21. Көпіршікті сұрыптауы (Bubble_sort) және оның ерекшеліктері

Көпіршікті сұрыптау алгоритмінің негізгі идеясы массивтің көрші элементтерін өзара қостап салыстырып қажет жағдайда орындарын ауыстыруда жатыр. Айқын болу үшін массивтің сол жағынан, яғни x₁элементінен бастайық және солдан оңға қарай жылжиық. Жылжу барысында x_i,x_i+1жұптарын екі екіден салыстырып отырып, бірінші қадамның соңында ең үлкен(ең кіші) элемент ең оң жақ шеткі орын алады. Процессті қайталаймыз, келесі қадамда да массивтің ең сол жақ шетінен бастаймыз, ал ең оң жақтағы, яғни n-ші орында тұрған элемент тұрақты орын алып және екінші қадамда процеске қатыспайтынын ескереміз.Әр қадамда бір элементтен шегеріліп отырады, яғни массивтің сұрыпталған оң жақ шеті оңнан солға қарай жылжып отырады. Процесс массивтің соңғы элементі(ең сол жақ шеткі) сұрыпталған массивте өзінің орнына тұрғанша қайталана береді.

Жоғарыда келтірілген «көпіршіктік сұрыптау» алгоритмінің негізінде массивті реттеуге қажетті салыстыру/ санының бағасын беруге болады. «Көпіршіктік сұрыптау» алгоритмі үшін салыстыру саны 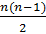тең екенін есептеу қиын емес. Осыған байланысты «көпіршіктік сұрыптау» алгоритмі күделілігі O(n²) болатын алгоритмдер класына жатады.

Алгоритмнің программалық нұсқасын келтірейік.

Procedure bubblesort (a, n);

....

Begin

for m:=n down to 2 do

begin r:=a[1];