Тест Голдфелда—Квандта

Вероятно, наиболее популярным формальным критерием является крите­рий, предложенный С. Голдфелдом и Р. Квандтом (Goldfeld, Quandt, 1956). При проведении проверки по этому критерию предполагается, что стандартное от­клонение (σ_i) распределения вероятностей u_i пропорционально значению х в этом наблюдении. Предполагается также, что случайный член распределен нор­мально и не подвержен автокорреляции.

Все n наблюдений в выборке упорядочиваются по величине х, после чего оцениваются отдельные регрессии для первых n ' и для последних n ' наблюде­ний; средние (n — 2 n) наблюдений отбрасываются. Если предположение отно­сительно природы гетероскедастичности верно, то дисперсия u в последних n' наблюдениях будет больше, чем в первых n ' и это будет отражено в сумме квад­ратов остатков в двух указанных «частных» регрессиях. Обозначая суммы квад­ратов остатков в регрессиях для первых n ' последних n ' наблюдений соответ­ственно через ESS₁ и ESS₂, рассчитаем отношение ESS₂/ESS₁, которое имеет F-распределение с (n '— k — 1) и (n '— k — 1) степенями свободы, где k — число объясняющих переменных в регрессионном уравнении. Мощность критерия за­ висит от выбора n ' по отношению к n. Основываясь на результатах некоторых проведенных ими экспериментов, С. Голдфелд и Р. Квандт утверждают, что n ' должно составлять порядка 11, когда n = 30, и порядка 22, когда n = 60. Если в модели имеется более одной объясняющей переменной, то наблюдения долж­ны упорядочиваться по той из них, которая, как предполагается, связана с σ _i, и n ' должно быть больше, чем k + 1 (где k — число объясняющих переменных).

Метод Голдфелда— Квандта может также использоваться для проверки на гетероскедастичность при предположении, что σ _i обратно пропорционально x_i. При этом используется та же процедура, что и описанная выше, но тестовой статистикой теперь является показатель ESS₁/ESS₂, который вновь имеет F-рас­пределение с (n '— k —1) и (n '— k —1) степенями свободы.

Тест Глейзера

Тест Глейзера позволяет несколько более тщательно рассмотреть характер гетероскедастичности. Мы снимаем предположение о том, что σ _i пропорцио­нально х_i, и хотим проверить, может ли быть более подходящей какая-либо другая функциональная форма, например

(8.4)

Чтобы использовать данный метод, следует оценить регрессионную зависи­мость у от х с помощью обычного МНК, а затем вычислить абсолютные вели­ чины остатков | | по функции (8.4) для данного значения у. Можно построить несколько таких функций, изменяя значение у. В каждом случае нулевая гипо­теза об отсутствии гетероскедастичности будет отклонена, если оценка β зна­чимо отличается от нуля. Если при оценивании более чем одной функции по­лучается значимая оценка β, то ориентиром при определении характера гете­роскедастичности может служить наилучшая из них.

4. Что можно сделать в случае гетероскедастичности?

Пусть σ _i — стандартное отклонение случайного члена в наблюдении i. В том случае если бы было известно σ_i для каждого наблюдения, можно было бы ус­транить гетероскедастичность, разделив каждое наблюдение на соответствую­щее ему значение σ. Тогда случайный член в i -м наблюдении становится рав­ным u_i / σ _i, и его теоретическая дисперсия представляется в виде:

что равняется:

Это выражение переписывается как

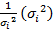
и, следовательно, оно равно единице. Таким образом, каждое наблюдение будет иметь случайный член, полученный из генеральной совокупности с единич­ной дисперсией, и модель будет гомоскедастичной. Теперь модель имеет вид:

, (8.5) что может быть переписано как

, (8.6)

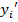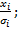
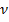где определяется как представляет собой — новая переменная, i -е наблюдение которой равно величина есть Следует отметить, что в данном уравнении не должно быть постоянного члена. Оценивая регрессион­ную зависимость у ' от 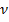и , мы получим эффективные оценки для α и β c несмещенными стандартными ошибками. Математическое доказательство того, что уравнение (8.6) даст более эффек­тивные оценки, чем уравнение (8.1), выходит за рамки нашего курса, но здесь можно дать простое интуитивное объяснение. Наблюдения с наименьшими зна­чениями σ_i будут наиболее полезными для определения истинной зависимости между у и х, поскольку величина случайного члена в них, как правило, наи­меньшая. Мы воспользуемся этим, оценивая так называемую взвешенную регрес­сию, придавая наибольшие веса наблюдениям самого «высокого качества», а наи­меньшие веса — соответственно, наблюдениям самого «низкого качества». Урав­нение (8.6) можно рассматривать как «взвешенный» вариант уравнения (8.1), где значения у и х были умножены на величины 1/σ_i, которые, конечно, тем больше, чем меньше σ_i.

Препятствием для этой процедуры является то, что вам почти наверняка бу­дут неизвестны фактические значения σ_i. Однако процедура будет применимой, если мы сможем подобрать некоторую величину, пропорциональную, по на­шему мнению, σ в каждом наблюдении, и разделим на нее обе части уравне­ния.

Допустим, есть основания предположить, что некоторая величина z про­порциональна σ_i и , где — некоторая константа. После деления на z уравнение принимает вид:

(8.7)

Дисперсия случайного члена представлена как

,

что равно 1 / ². Следовательно, эта величина постоянна для всех наблюдений, и проблема устранена.

Например, может оказаться целесообразным предположить, что σ приблизительно пропорционально х, как в критерии Голдфелда—Квандта. Если после этого мы разделим каждое наблюдение на соответствующее ему значение х, то уравнение (8.1) примет вид:

(8.8)

и при этом, если повезет, новый случайный член u/ х будет иметь постоянную дисперсию. Затем мы оцениваем регрессионную зависимость у / х от 1/ х, вклю­чив в уравнение постоянный член. Коэффициент при 1/ х будет эффективной оценкой α, а постоянный член — эффективной оценкой β. В примере с расхо­дами на образование, рассмотренном в предыдущем пункте, зависимой пере­менной будут государственные расходы на образование как доля ВВП, а объяс­няющей переменной — обратная к ВВП величина.

Иногда в нашем распоряжении может оказаться несколько переменных, каждую из которых можно использовать для масштабирования уравнения. В при­мере с расходами на образование альтернативной переменной является числен­ность населения страны (Р). Разделив обе части уравнения (8.1) на эту величи­ну, получаем:

, (8.9)

и мы снова надеемся на то, что случайный член u _i / P _i будет иметь постоянную дисперсию для всех наблюдений. Таким образом, теперь оценивается регресси­онная зависимость государственных расходов на образование на душу населе­ния от ВВП на душу населения и обратной величины от численности населе­ния, причем на этот раз без постоянного члена.

На практике имеет смысл попробовать использовать несколько разных пе­ременных для масштабирования наблюдений и сравнить затем результаты. Если каждый раз получаются сходные результаты и тесты не дают оснований откло­нять нулевую гипотезу о гомоскедастичности, то проблему можно считать ре­шенной.