Этапы и цели компьютерного моделирования

Рассмотрим процесс компьютерного математического моделирования, включающий численный эксперимент с моделью.

Моделирование занимает центральное место в исследовании объекта, процесса, явления. Оно позволяет обоснованно принимать решение: как совершенствовать объекты (процессы), надо ли создавать новые, как изменять процессы управления и, в конечном итоге, как менять окружающий мир в лучшую сторону.

Прежде чем браться за какую-либо работу, нужно четко представить себе отправной и конечный пункты деятельности, а также примерные ее этапы. То же можно сказать о моделировании.

Отправной пункт здесь – прототип. Им может быть существующий или проектируемый объект либо процесс.

Конечный этап – принятие решения. На этом этапе мы либо создаем новый объект (процесс), модель которого мы исследовали, либо улучшаем существующий, либо получаем о нем дополнительную информацию.

Рассмотрим процесс решения задачи на компьютере на следующем примере: изучим полет ядра, вытолкнутого легкоатлетом. Построим содержательную модель, в которой рассмотрим движение ядра в поле тяготения Земли. В этой модели рассматриваются только те параметры, которые характеризуют движение ядра (скорость и координаты), и отвлекаемся от других параметров (температура ядра, его цвет и т. д.).

Теперь построим математическую модель, которая основана на некоторых упрощениях, и это делает этап построения математической модели весьма ответственным, ведь неправильно выбранная модель приведет к неверным результатам.

Существующая физическая система описывается с помощью упрощенной математической модели. Ядро является материальной точкой, сопротивлением воздуха, скоростью ветра и параметрами спортсмена пренебрегаем, ускорение свободного падения считаем постоянным g= 9,8 м/с2. Ядро выталкивается спортсменом со скоростью V под углом к горизонту.

Математическая модель описывает объект моделирования с помощью уравнений.

Получим формулы зависимости координат снаряда от времени, учитывая, что по оси X движение равномерное, а по оси Y – равноускоренное:

Теперь построим информационную модель и алгоритм. На этом этапе необходимо определить, какие величины являются аргументами, а какие – результатами алгоритма, а также определить тип этих величин. В нашем случае аргументами являются: угол вылета снаряда а, его начальная скорость V и время полета t. Результатом являются координаты X и Y. Все они являются переменными вещественного типа. Построим алгоритм, который позволяет определять значения результатов при различных значениях аргументов. Построенный алгоритм записываем в виде блок-схемы:

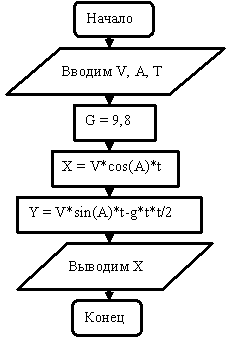
Рисунок 9.5. Блок-схема алгоритма расчета координат полета снаряда

Теперь можно проводить компьютерный эксперимент. Для этого необходимо загрузить программу в оперативную память компьютера и запустить на выполнение. Компьютерный эксперимент обязательно включает в себя анализ полученных результатов, на основании которого могут корректироваться все этапы решения задачи (математическая модель, алгоритм, программа).

Контрольные вопросы

1. Что такое модель?

2. Для чего используются модели?

3. Что такое моделирование?

4. Как классифицируются модели?

5. Какие этапы проходит процесс создания модели?

6. Какие виды моделирования различают?

7. Какие модели характеризуют информационное моделирование?

8. Что такое формализация?

9. Какими чертами должен обладать знак?

10. В чем заключается цель компьютерного моделирования?

11. Что понимается под компьютерной моделью?

12. Каковы основные функции и этапы компьютерного моделирования?

Глава 10