Общая характеристика распределительной задачи

Распределительные задачи связаны с распределением ресурсов по работам, которые необходимо выполнить. Задачи этого класса возникают тогда, когда имеющихся в наличии ресурсов не хватает для выполнения каждой работы наиболее эффективным образом. Поэтому целью решения задачи, является отыскание такого распределения ресурсов по работам, при котором либо минимизируются общие затраты, связанные с выполнением работ, либо максимизируется получаемый в результате общий доход.

Большинство распределительных задач можно представить в виде матриц, приведённых в таблице 5.1.1.

Таблица 5.1.1

Ресурсы	Работы, которые нужно выполнить	Объём имеющихся ресурсов
J1	J2	…	Jj	…	Jn
R1 R2 … Ri … Rm	C1,1 C2,1 … Ci,1 … Cm,1	C1,2 C2,2 … Ci,2 … Cm,2	… … … … … …	C1,j C2,j … Ci,j … Cm,j	… … … … … …	C1,n C2,n … Ci,n … Cm,n	b1 b2 … bi … bm
Объём требуемых ресурсов	а1	а2	…	aj	…	an

Элементы C_i,j , стоящие в клетках матрицы, соответствуют затратам или доходу, отвечающим выделению, одной единицы ресурса R_i на работу J_j. Величины C_i,j могут быть зависимыми и независимыми. Так, например, затраты, обусловленные назначением одной автомашины на некоторый маршрут доставки грузов, не зависят от того какие машины назначены на обслуживание других маршрутов. В то же время при распределении средств между подразделениями фирмы доход от затрат определённого количества денег одним её подразделением (скажем производством) обычно зависит от того, какие средства будут затрачены другими подразделениями (скажем отделом сбыта). В теории распределения рассматриваются преимущественно задачи с независимыми затратами и доходами. Это объясняется не тем, что такие задачи более важны, а лишь тем, что для них значительно легче строить модели и получать решения.

Если затраты (или доход), определяемые объёмом Х_i,j ресурса I, выделенного на выполнение работы J_i, равны Х_i,j*C_i,j , то имеем линейную распределительную задачу.

Основные методы решения распределительных задач, в частности линейного программирования, построены на допущении, что объёмы, имеющихся в наличии ресурсов (b_i), требуемые объёмы (a_j) и затраты (C_i,j) точно известны.

Если общий объём наличных ресурсов _i (i=1…m) равен общей потребности в них ∑a_j (i=1…n), то имеет место сбалансированная (закрытая) распределительная задача. Если же ∑a_j≠∑b_i, то задача называется несбалансированной (открытой). Если ресурсы можно разделить между работами, то некоторые работы можно выполнять с помощью различных комбинаций ресурсов. Если работы и ресурсы измеряются в единицах одной и той же шкалы, то такие задачи обычно называют транспортными или задачами разложения. Если же работы и ресурсы выражаются в различных единицах измерения, то задача называется общей разделительной задачей. Таким образом транспортная задача является частным случаем общей распределительной задачи.

5.2 Транспортная задача.

Транспортная задача ставится следующим образом: имеется m пунктов отправления А₁, А₂, …,А_m, в которых сосредоточены запасы каких-то однородных грузов в количестве соответственно а₁, а_2,…,а_m единиц. Имеется n пунктов назначения B₁, B₂,…,B_n подавшие заявки соответственно на b₁,b₂,…,b_n единиц груза. Известны стоимости C_i,j перевозки единицы груза от каждого пункта отправления А_i до каждого пункта назначения B_j. Все числа C_i,j , образующие прямоугольную таблицу заданы. Требуется составить такой план перевозок(откуда, куда и сколько единиц поставить), чтобы все заявки были выполнены, а общая стоимость всех перевозок была минимальна.

Рассмотрим сначала решение закрытой транспортной задачи, т.е. когда сумма всех заявок равна сумме всех запасов.

Решение транспортной задачи начинается с нахождения опорного плана. Для этого существуют различные способы. Например, способ “северо-западного угла”, способ минимальной стоимости по строке, способ минимальной стоимости по столбцу и способ минимальной стоимости таблицы. Рассмотрим простейший, так называемый способ северо-западного угла. Пояснить его проще всего будет на конкретном примере:

Условия транспортной задачи заданы транспортной таблицей.

Таблица 5.2.1

ПН ПО	В1	В2	В3	В4	В5	Запасы аi
А1
А2
А3
А4
Заявки bj

Будем заполнять таблицу перевозками постепенно начиная с левой верхней ячейки («северо-западного угла» таблицы). Будем рассуждать при этом следующим образом. Пункт В₁ подал заявку на 18 единиц груза. Удовлетворим эту заявку за счет запаса 48, имеющегося в пункту А₁, и запишем перевозку 18 в клетке (1,1). После этого заявка пункта В₁ удовлетворена, а в пункте А₁ осталось еще 30 единиц груза. Удовлетворим за счёт них заявку пункта В₂ (27 единиц), запишем 27 в клетке (1,2); оставшиеся 3 единицы пункта А₁ назначим пункту В₃. В составе заявки пункта В₃ остались неудовлетворёнными 39 единиц. Из них 30 покроем за счёт пункта А₂, чем его запас будет исчерпан, и ещё 9 возьмём из пункта А₃. Из оставшихся 18 единиц пункта А₃ 12 выделим пункту В₄; оставшиеся 6 единиц назначим пункту В₅, что вместе со всеми 20 единицами пункта А₄ покроет его заявку. На этом распределение запасов закончено; каждый пункт назначения получил груз согласно своей заявки. Это выражается в том, что сумма перевозок в каждой строке равна соответствующему запасу, а в столбце – заявке. Таким образом, нами сразу же составлен план перевозок, удовлетворяющий балансовым условиям. Полученное решение является опорным решением транспортной задачи:

Таблица 5.2.2

ПН ПО	В1	В2	В3	В4	В5	Запасы ai
А1
А2
А3
А4
Заявки bj

Составленный нами план перевозок, не является оптимальным по стоимости, так как при его построении мы совсем не учитывали стоимость перевозок C_i,j .

Другой способ – способ минимальной стоимости по строке – основан на том, что мы распределяем продукцию от пункта А_i не в любой из пунктов В_j, а в тот, к которому стоимость перевозки минимальна. Если в этом пункте заявка полностью удовлетворена, то мы убираем его из расчётов и находим минимальную стоимость перевозки из оставшихся пунктов В_j. Во всем остальном этот метод схож с методом “северо-западного угла”. В результате, опорный план, составленный способом минимальной стоимости по строке выглядит как показано в таблице 5.2.2.

При этом методе может получиться, что стоимости перевозок C_i,j и C_i,k от пункта А_i к пунктам В_j и В_k равны. В этом случае, с экономической точки зрения, выгоднее распределить продукцию в тот пункт, в котором заявка больше. Так, например, в строке 2: С_2,1=С_2,4, но заявка b₁ больше заявки b₄, поэтому 4 единицы продукции мы распределим в клетку (1,2).

Таблица 5.2.3

ПН ПО	В1	В2	В3	В4	В5	Запасы аi
А1
А2
А3					0
А4
Заявки bj

Способ минимальной стоимости по столбцу аналогичен предыдущему способу. Их отличие состоит в том, что во втором способе мы распределяем продукцию от пунктов В_i к пунктам А_j по минимальной стоимости C_j,i. Опорный план, составленный способами минимальных стоимостей, обычно более близок к оптимальному решению. Так в нашем примере общие затраты на транспортировку по плану, составленному первым способом Z(х₀)=1039, а по второму - Z(х₀)=723.

Клетки таблицы, в которых стоят ненулевые перевозки, являются базисными. Их число должно равняться m+n-1. Необходимо отметить также, что встречаются такие ситуации, когда количество перевозок равное нулю. Так,например, в таблице5.2.3.:

m+n-1=4+5-1=8,

а базисных клеток 7, поэтому нужно в одну из клеток строки 3 или столбца 2 поставить значение ”0”. Например в клетку (3,5).

Составляя план по способам минимальных стоимостей в отличии от плана по способу “северо-западного угла” мы учитываем стоимости перевозок C_i,j, но все же не можем утверждать, что составленный нами план является оптимальным.

Теперь попробуем улучшить план, составленный способом “северо-западного угла”. Перенесём, например, 18 единиц из клетки (2,3) в клетку (1,3). Получим новый план. Подсчитав стоимость опорного плана (она ровняется 1039) и стоимость нового плана 126 единиц меньше. Таким образом за счёт циклической перестановки 18 единиц груза из одних клеток в другие нам удалось понизить стоимость плана:

Таблица 5.2.4

ПН ПО	В1	В2	В3	В4	В5	Запасы аi
А1
А2
А3
А4
Заявки bj

На этом способе уменьшения стоимости в дальнейшем и будет основан алгоритм оптимизации плана перевозок. Циклом в транспортной задаче мы будем называть несколько занятых клеток, соединённых замкнутой ломанной линей, которая в каждой клетке совершает поворот на 90⁰.

Существует несколько вариантов цикла:

1.) 2.) 3.)

Рис.5.1.

Нетрудно убедиться, что каждый цикл имеет четное число вершин и значит, четное число звеньев (стрелок). Условимся отмечать знаком «+» те вершины цикла, в которых перевозки необходимо уменьшить. Цикл с отмеченными вершинами будем называть «означенными». Перенести какое-то количество единиц груза по означенному циклу - это значит увеличить перевозки, стоящие в положительных вершинах цикла, на это количество единиц, а перевозки, стоящие в отрицательных вершинах уменьшить на то же количество. Очевидно, при переносе любого числа единиц по циклу равновесие между запасами и заявками не меняется: по прежнему сумма перевозок в каждой строке равна запасам этой строки, а сумма перевозок в каждом столбце – заявке этого столбца. Таким образом при любом циклическом переносе, оставляющем перевозки неотрицательными допустимый план остаётся допустимым. Стоимость же плана при этом может меняться: увеличиваться или уменьшаться. Назовём ценой цикла увеличение стоимости перевозок при перемещении одной единицы груза по означенному циклу. Очевидно цена цикла равна алгебраической сумме стоимостей, стоящих в вершинах цикла, причём стоящие в положительных вершинах берутся со знаком “+”, а в отрицательных со знаком “-”. Обозначим цену цикла через γ. При перемещении одной единицы груза по циклу стоимость перевозок увеличивается на величину γ. При перемещении по нему k единиц груза стоимость перевозок увеличится на kγ. Очевидно, для улучшения плана имеет смысл перемещать перевозки только по тем циклам, цена которых отрицательна. Каждый раз, когда нам удаётся совершить такое перемещение стоимость плана уменьшается на соответствующую величину kγ. Так как перевозки не могут быть отрицательными, мы будем пользоваться только такими циклами, отрицательные вершины которых лежат в базисных клетках таблицы, где стоят положительные перевозки. Если циклов с отрицательной ценой в таблице больше не осталось, это означает, что дальнейшее улучшение плана невозможно, то есть оптимальный план достигнут.

Метод последовательного улучшения плана перевозок и состоит в том, что в таблице отыскиваются циклы с отрицательной ценой, по ним перемещаются перевозки, и план улучшается до тех пор пока циклов с отрицательной ценой уже не останется. При улучшении плана циклическими переносами, как правило, пользуются приемом, заимствованным из симплекс-метода: при каждом шаге (цикле) заменяют одну свободную переменную на базисную, то есть заполняют одну свободную клетку и взамен того освобождают одну из базисных клеток. При этом общее число базисных клеток остается неизменным и равным m + n – 1. Этот метод удобен тем, что для него легче находить подходящие циклы.

Можно доказать, что для любой свободной клетке транспортной таблице всегда существует цикл и притом единственный, одна из вершин которого лежит в этой свободной клетке, а все остальные в базисных клетках. Если цена такого цикла, с плюсом в свободной клетке, отрицательна, то план можно улучшить перемещением перевозок по данному циклу. Количество единиц груза k которое можно переместить, определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла (если переместить большее число единиц груза, возникнут отрицательные перевозки).

Примененный выше метод отыскания оптимального решения транспортной задачи называется распределенным; он состоит в непосредственном отыскании свободных клеток с отрицательной ценой цикла и в перемещении перевозок по этому циклу.

Распределительный метод решения транспортной задачи, с которым мы познакомились обладает одним недостатком: нужно отыскивать циклы для всех свободных клеток и находить их цены. От этой трудоемкой работы нас избавляет специальный метод решения транспортной задачи, который называется методом потенциалов.

Пример. Решить распределенным методом транспортную задачу, исходные данные которой приведены в табл. 5.2.5.

Таблица 5.2.5

bj ai

Р е ш е н и е. Строим начальное опорное решение методом минимальной стоимости (табл. 5.2.6)

С=

Затем вычисляем значения целевой функции на нем:

Z(X₁)=20·1+30·5+10·8+40·15=850

Таблица 5.2.6

bj ai
	- 20		0 +
	4 +	- 30
		+ 10	40 -

Находим цикл для свободной клетки (1,2) таблицы,, он включает клетки (1,2), (1,3), (3,3), (3,2). Вычисляем оценку Δ₁₂=(3+15)-(2+8)=8. Так как Δ₁₂=8>0, переходим к следующей свободной клетке (2,1). Для нее цикл таков: (2,1), (1,1), (1,3), (3,3), (3,2), (2,2). Оценка Δ₂₁=(4+2+8)-(1+15+5)=14-21= -7. Так как Δ₂₁= - 7<0, определяем величину груза, перераспределяемого по циклу, 0=min {20, 40, 30} = 20. Приращение целевой функции ΔZ = -7·20= -140. Получаем новое опорное решение X₂ (табл. 5.2.7). Значение целевой функции на нем

Z(X₂)=20·2+20·4+10·5+30·8+20·15=710

Таблица 5.2.7

bj ai
		- 10	+
		+ 30	20 -

Вычисляем Δ₁₁=(1+15+5) – (2+8+4)=7>0, Δ₁₂=(3+15) – (2+8)=8>0, Δ₂₃=(7+8) – (5+15)= -5<0, Δ₃₁=(6+5) – (4+8)= -1<0. Оценки можно вычислять до первой отрицательной. Так как Δ₂₃= -5<0, осуществляем сдвиг по циклу (2,3), (3,3), (3,2), (2,2) на величину 0=min {10, 20} = 10. Приращение целевой функции ΔZ= -5·10= -50. Поучаем третье опорное решение X₃ (табл. 5.2.8).

Значение целевой функции на нем

Z(X₃)=20·2+20·4+10·7+40·8+10·15=660

Таблица 5.2.8

bj ai
	20-		10 +
	+		10 -

Вычисляем оценки для свободных клеток: Δ₁₁=(1+7) - (2+4) = 2>0, Δ₁₂=(3+15) – (2+8) = 8>0, Δ₂₂=(5+15) – (7+8) = 5>0, Δ₃₁=(6+7) – (4+15) = -6<0. Так как Δ₃₁= -6<0, осуществляем сдвиг по циклу (3,1), (2,1), (2,3), (3,3) на величину 0=min {20, 10} = 10. Приращение целевой функции ΔZ= -6·10 = -60. Получаем четвертное опорное решение X₄ (табл. 5.2.9). Значение целевой функции на нем

Z(X₄)=20·2+10·4+20·7+10·6+40·8=600.

Таблица 5.2.9

bj ai
	- 10	+
	+ 10	40 -

Вычисляем оценки для свободных клеток Δ₁₁=(1+7) – (2+4)=2>0, Δ₁₂=(3+7+6) – (2+4+8)=2>0, Δ₂₂=(5+6) – (4+8)= -1<0. Так как Δ₁₂= -1<0, осуществляем сдвиг по циклу (2,2), (3,2), (3,1), (2,1) на величину 0=min {10, 40}=10. Приращение целевой функции ΔZ= = -1·10= -10. Получаем пятое опорное решение X₅ (табл. 5.2.10).

Таблица 5.2.10

bj ai

Значение целевой функции на нем

Z(X₅)=20·2+10·5+20·7+20·6+30·8=590.

Вычисляем оценки для свободных клеток: Δ₁₁=(1+7) – (2+4)=2>0, Δ₁₂=(3+7) – (2+5)=3>0, Δ₃₃=(15+5) – (7+8)=5>0. Все оценки для свободных клеток положительные, следовательно, решение оптимально.

Ответ: min Z(X)=590 при X= •

Этот метод позволяет автоматически выделять циклы с отрицательной ценой и определять их цены.

Пусть имеется транспортная задача с балансовыми условиями

Σ x_i,j = a_i (i=1..m; j=1..n);

Σ x_i,j = b_j (j=1..n; 1..m).

Причем ∑a_i=∑b_i

Стоимость перевозки единицы груза из А_i в В_j равна C_i,j; таблица стоимостей задана. Требуется найти план перевозок (x_i,j,), который удовлетворял бы балансовым условиям и при этом стоимость всех перевозок была минимальна.

Идея метода потенциалов для решения транспортной задачи сводится к следующему. Представим себе что каждый из пунктов оправления A_i вносит за перевозку единицы груза (все равно куда) какую-то сумму α_i; в свою очередь каждый из пунктов назначения В_j также вносит за перевозку груза (куда угодно) сумму β_j. Эти платежи передаются некоторому третьему лицу («перевозчику»). Обозначим α_i+β_j=c_i,j (i=1..m; j=1..n) и будем называть величину с_i,j «псевдостоимостью» перевозки единицы груза из А_i в В_j. Заметим, что платежи α_i и β_j не обязательно должны быть положительными; не исключено, что «перевозчик» сам платит тому или другому пункту какую-то премию за перевозку. Также надо отметить, что суммарная псевдостоимость любого допустимого плана перевозок при заданных платежах (α_i и β_j) одна и та же и от плана к плану не меняется.

До сих пор мы никак не связывали платежи (α_i и β_j) и псевдостоимости с_i,j с истинными стоимостями перевозок С_i,j. Теперь мы установим между ними связь. Предположим, что план (x_i,j,) невырожденный (число базисных клеток в таблице перевозок равно (m+n-1). Для всех этих клеток x_i,j,>0. Определим платежи (α_i и β_j) так, чтобы во всех базисных клетках псевдостоимости были равны стоимостям:

α_i+β_j=C_i,j=c_i,j,

а для всех свободных клеток (X_i,j=0)

α_i+β_j≤C_i,j

то план является оптимальным и никакими способами улучшен быть не может. Нетрудно показать, что это теорема справедлива также для выраженного плана, и некоторые из базисных переменных ровны нулю. План обладающий свойством:

C_i,j=c_i,j (для всех базисных клеток) 5.2.1

C_i,j?c_i,j (для всех свободных клеток) 5.2.2

называется потенциальным планом, а соответствующие ему платежи (α_i и β_j) - потенциалами пунктов А_i в В_j (i=1,…,m;j=1,…,n). Пользуясь этой терминологией вышеупомянутую теорему можно сформулировать так: Всякий потенциальный план является оптимальным. Итак, для решения транспортной задачи нам нужно одно – построить потенциальный план. Оказывается его можно построить методом последовательных приближений, задаваясь сначала какой-то произвольной системой платежей, удовлетворяющей условию 5.2.1. При этом в каждой базисной клетке получится сумма платежей, равная стоимости перевозок в данной клетке; затем, улучшая план следует одновременно менять систему платежей. Так, что они приближаются к потенциалам. При улучшении плана нам помогает следующее свойство платежей и псевдостоимостей: Какова бы ни была система платежей (α_i в β_j) удовлетворяющая условию 5.2.1, для каждой свободной клетки цена цикла перерасчета равна разности между стоимостью и псевдостоимостью в данной клетке: γ_i,j=c_i,j-C_i,j.

Таким образом при использовании методом потенциалов для решения транспортной задачи отпадает наиболее трудоемкий элемент распределительного метода: поиски циклов с отрицательной ценой.

Процедура построения потенциального (оптимального) плана состоит в следующем.

В качестве первого приближения к оптимальному плану берется любой допустимый план (например, построенный способом минимальной стоимости по строке). В этом плане m+n-1 базисных клеток, где m – число строк, n – число столбцов транспортной таблицы. Для этого плана можно определить платежи (α_i в β_j), так, чтобы в каждой базисной клетке выполнялось условие:

α_i+β_j=с_i,j (5.2.3)

Уравнений (5.2.3) всего m+n-1, а число неизвестных равно m+n. Следовательно, одну из этих неизвестных можно задать произвольно (например, равной нулю). После этого из m+n-1 уравнений (5.2.3) можно найти остальные платежи α_i и β_j, а по ним вычислить псевдостоимости: С_i,j =α_i+β_j для каждой свободной клетки.

Таблица 5.2.11

ПН ПО	В1	В2	В3	В4	В5	αi
А1	c=7	c=6			c=6
А2		c=5	c=4	c=5		-1
А3	c=8		c=6	c=7
А4		5 c=6	4 c=5		c=6
βj

Если оказалось, что все эти псевдостоимости не превосходят стоимостей

С_i,j≤ с_i,j,

то план потенциален и, значит, оптимален. Если же хотя бы в одной свободной клетке псевдостоимотсь больше стоимости (как в нашем примере), то план не является оптимальным и может быть улучшен переносом перевозок по циклу, соответствующему данной свободной клетке. Цена этого цикла ровна разности между стоимостью и псовдостоимостью в этой свободной клетке.

В таблице 5.2.11 мы получили в двух клетках С_i,j≤ с_i,j, теперь можно поострить цикл в любой из этих двух клеток. Выгоднее всего строить цикл в той клетке, в которой разность С_i,j- с_i,j максимальна. В нашем случае в обоих клетках разность одинакова (равна 1), поэтому, для построения цикла выберем, например, клетку (4,2):

Таблица 5.2.12

ПН ПО	В1	В2	В3	В4	В5	αi
А1
А2	6 +				5 -	-1
А3		7 -			7 +
А4	7 -	5 + x
βj

Теперь будем перемещать по циклу число 14, так как оно является минимальным из чисел, стоящих в клетках, помеченных знаком -. При перемещении мы будем вычитать 12 из клеток со знаком – и прибавлять к клеткам со знаком +.

После этого необходимо подсчитать потенциалы α_i и β_j и цикл расчетов повторяется.

Итак, мы приходим к следующему алгоритму решения транспортной задачи методом потенциалов:

- взять любой опорный план перевозок, в котором отмечены m+n-1 базисных клеток (остальные клетки свободные);

- определить для этого плана платежи (α_i и β_j) исходя из условия, чтобы в любой базисной клетке псевдостоимости были равны стоимостям. Один из платежей можно назначить произвольно, например, положить равным нулю.

- подсчитать псевдостоимости С_i,j =α_i+β_j для всех свободных клеток. Если окажется, что все они не превышают стоимостей, то план оптимален.

- если хотя бы в одной свободной клетке псевдостоимость превышает стоимость, следует приступить к улучшению плана путем переброски перевозок по циклу, соответствующему любой свободной клетке с отрицательной ценой (для которой псевдостоимость больше стоимости).

- после этого заново подсчитываются платежи и псевдостоимости, и, если план еще не оптимален, процедура улучшения продолжается до тех пор, пока не будет найден оптимальный план.

Так в нашем примере после 2 циклов расчетов получим оптимальный план вида:

X₂= ,где 0^x – базисный нуль.

При этом стоимость всей перевозки изменялась следующим образом:

Z(X₀)=703

Z(X)=709

Z(X₂)=Zmin=703.

Следует отметить так же, что оптимальный план может иметь и другой вид, но его стоимость останется такой же Z_min=703.

Однако на практике чаще встречаются задачи с неправильным балансом.

1. Пусть суммарные запасы поставщиков превосходят суммарные запасы потребителей, т.е.

>

Очевидно, что в этом случае при составлении оптимального плана перевозок часть запасов поставщиков, равная

b_n+1= -

останется не вывезенной. Поэтому в системе ограничений транспортной задачи первую группу уравнений (i Є1, ) следует заменить неравенствами вида «≤».

Вторая группа уравнений остается без имени, так как запросы всех потребителей удовлетворяются полностью. Для приведения к канонической форме в полученные неравенства вводят дополнительные переменные x_1(n+1), x_2(n+1),…,x_m(n+1). В результате первые m ограничений задачи принимают вид

+x_i(n+1)=a_i, i=1,2,..,m

В целевую функцию дополнительные переменные не входят (входят с нулевыми коэффициентами). Математическая модель задачи принимает вид

Z(X)= ·x_i(n+1) →min, (5.2.4)

+x_i(n+1)=a_i, i=1,2,…,m, (5.2.5)

=b_j, j=1,2,…,n, (5.2.6)

x_ij≥0, i=1,2,…,m, j=1,2,…,n+1. (5.2.7)

Запишем необходимое и достаточное условие разрешимости задачи:

,

отсюда

.

Следовательно, чтобы задача в рассматриваемом случае имела решение, необходимо ввести фиктивного потребителя с запросами b_n+1 равными разности суммарных запасов поставщиков и запросов потребителей, и нулевыми стоимостями перевозок единиц груза c_i(n+1)=0 i.

2. Аналогично в случае, когда суммарные запросы потребителей превосходят суммарные запасы поставщиков, т.е. <

часть запросов потребителей, равная a_m+1= -

останется неудовлетворенной. Поэтому вторая группа уравнений системы ограничений (j Є1. 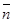) транспортной задачи заменяется неравенствами вида «≤».

После введения дополнительных переменных x_(m+1)1, x_(m+1)2,, …, x_(m+1)n в эти неравенства математическая модель задачи примет вид

Z(X)= ·x_(m+1)j →min, (5.2.8)

i=1,2, …, m, (5.2.9)

+x_(m+1)j=b_i, i=1,2,…,n. (5.2.10)

x_ij≥0, i=1,2,…,m+1, j=1,2,…,n. (5.2.11)

Для того чтобы задача имела решение, необходимо и достаточно, чтобы

,

отсюда

.

Следовательно, чтобы в этом случае задача имела решение, необходимо ввести фиктивного поставщика с запасами a_m+1, равными разности суммарных запросов потребителей и запасов поставщиков, и нулевыми стоимостями перевозок единиц груза с_(m+1)j=0 j.

Транспортная задача с ограничениями на пропускную способность.

Пусть требуется при решении транспортной задачи ограничить перевозки от поставщика с номером l к потребителю с номером k. Возможны ограничения двух типов: 1) x_lk≥a; 2) x_lk≤b, где a и b – постоянные величины.

1. Если x_lk≥a, то необходимо прежде, чем решать задачу, сократить запасы l-го поставщика и запросы k-го потребителя на величину а (зарезервировать перевозку x_lk≥a). После решения задачи в оптимальном решении следует увеличить объем перевозки x_lk на величину a..

2. Если x_lk≤b, то необходимо вместо k-го потребителя с запросами b_k ввести двух других потребителей. Один из них с номером k должен иметь запросы b_k=b, а другой с номером n+1 – запросы b_n+1=b_k-b. Стоимости перевозок для этих потребителей остаются прежними, за исключением стоимости c_l(n+1), которая принимается равной сколь угодно большому числу М (М>>1). После получения оптимального решения величины грузов, перевозимых к (n+1)-му потребителю, прибавляются к величинам перевозок k-го потребителя. Так как c_l(n+1)=M – самая большая стоимость перевозки, то в оптимальном решении клетка с номером (l,n+1) останется пустой, x_l(n+1)=0 и объем перевозки x_lk не превзойдет b.

Пример. Решить транспортную задачу, исходные данные которой приведены в табл. 5.3.1, при дополнительных условиях: объем перевозки груза от l-го поставщика 2-му потребителю должен быть не менее 100 единиц (x₁₂≥100), а от 3-го 1-му не более 200 единиц (x₃₁≤200).

Таблица 5.3.1

bj ai

Р е ш е н и е. Для того чтобы в оптимальном решении объем перевозки x₁₂ был не менее 100 единиц, при решении задачи будем предполагать, что запасы 1-го поставщика а₁ и запросы 2-го потребителя b₂ меньше фактических на 100 единиц. После получения оптимального решения объем перевозки x₁₂ увеличим на 100 единиц.

Для того чтобы удовлетворить требованию x₃₁≤200, вместо 1-го потребителя введем двух других. Один из них под прежним первым номером имеет запасы b₁=200 единиц и прежние стоимости перевозок единиц груза. Другому присвоим четвертый номер. Его запросы равны b₄=500-200=300 единиц и стоимости перевозок единиц груза те же, что и у 1-го потребителя за исключением с₃₄, которую примем равной сколь угодно большому числу М, т.е. с₃₄=М. После нахождения оптимального решения задачи объемы перевозок для 4-го потребителя необходимо прибавить к соответствующим объемам перевозок для 10го потребителя.

В результате указанных преобразований таблица исходных данных задачи будет иметь вид, представленный в табл. 5.3.2.

Таблица 5.3.2

bj ai
				M

Далее задачу решаем обычным методом потенциалов. Проверяем выполнение необходимого и достаточного условия существования решения задачи. Находим суммарные запасы поставщиков и запросы потребителей:

а₁+а₂+а₃=100+300+500=900;

b₁+b₂+b₃+b₄=200+300+300+300=1100.

Задача с неправильным балансом. Вводим фиктивного поставщика с запасами а₄=1100-900=200.

Составляем начальное опорное решение X₁ методом минимальной стоимости. Записываем матрицу стоимостей С:

С=

2 4 6

Кружочками в матрице С отмечены минимальные элементы, а цифрами рядом со строками и столбцами – порядок исключения из рассмотрения поставщиков и потребителей.

Таблица 5.3.3

X₁ v₁=1 v₂=0 v₃=1 v₄=1

bj ai
		-	-
	-	-	-	+
	5 +		-	M -
		-	+	-

u₁=0

u₂=1

u₃=7

u₄ = -1

Полученное решение X₁ имеет m+n-1=4+4-1=7 базисных переменных. Вычисляем значение целевой функции на этом опорном решении:

Z(X₁)=100·1+100·2+200·2+300·7+200·8+100·0+100·0=4400.

Для проверки оптимальности опорного решения находим потенциалы. Записываем систему уравнений для нахождения потенциалов и решаем ее:

Система состоит из семи уравнений и имеет восемь переменных. Так одно число неизвестных на единицу больше числа уравнений, то одному из потенциалов можно задать значение произвольно: пусть u₁=0. Остальные потенциалы однозначно находятся из системы уравнений:

u₁=0;

v₁=1-u=1-0=1;

u₂=2-v₁=2-1=1;

v₄=2-u₂=2-1=1;

u₄=0-v₄=0-1=-1;

v₃=0-u₄=0-(-1)=1;

u₃=8-v₃=8-1=7;

v₃=7-u₃=7-7=0.

Находим оценки для свободных клеток таблицы:

Δ₁₂=0+0-5= -5 <0; Δ₁₃=0+1-6= -5<0; Δ₁₄=0+1-1=0;

Δ₂₂=1+0-6= -5<0; Δ₂₃=1+1-7= -5<0; Δ₃₁=7+1-3=5>0;

Δ₃₄=7+1-M<0; Δ₄₁=-1+1-0=0; Δ₄₂=-1+0-0= -1<0.

Опорное решение неоптимальное, так как имеется положительная оценка Δ₃₁=5 для клетки (3,1). Отмечаем эту клетку знаком «+». Находим цикл для улучшения опорного решения (см. табл. 5.3.3). Определяем величину груза для перераспределения по циклу 0=min{11, 200, 100}=100. Осуществляем сдвиг по циклу на величину 0=100. Получаем второе опорное решение X₂ (табл. 5.3.4)

Таблица 5.3.4

X₂ v₁=1 v₂=5 v₃=6 v₄=1

bj ai
				M -
	-	-		-

u₁=0

u₂=1

u₃=2

u₄= -6

В табл. 5.3.4 также записаны потенциалы и оценки для свободных клеток. Решение X₂ оптимальное, так как все оценки неположительные. Запишем оптимальное решение исходной задачи. Для этого увеличим объем перевозки x₁₂ на 100 единиц и объединим объемы перевозок 4-го потребителя с объемами перевозок 1-го потребителя.

Получим

X*= •

Вычислим значение целевой функции на этом решении:

Z(X*)=100·1+100·5+300·2+100·3+300·7+100·8=4400.

Ответ: min Z(X)=4400 при X*= •

В некоторых задачах требуется запретить перевозки от отдельных поставщиков отдельным потребителям. В таких случаях либо зачеркивают клетку таблицы транспортной задачи, либо назначают соответствующую этой клетке стоимость перевозки единицы груза сколь угодно большой, равной М>>1. В остальном задача решается обычным способом. Для разрешимости данной задачи необходимо существование начального опорного решения.

Транспортная задача по критерию времени.

Задача по критерию времени возникает при перевозке срочных грузов. Как и в обычной транспортной задаче, имеется m поставщиков с запасами однородного груза в количестве а_1, а₂, …, а_m и n потребителей, которым этот груз должен быть доставлен в объеме b₁, b₂, …, b_n. Известно t_ij, i=1, 2, …, m, j=1, 2, …, n – время, за которое груз доставляется от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок груза, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и наибольшее время доставки всех грузов является минимальным.

Составим математическую модель этой задачи. Обозначим x_ij – объем перевозимого груза от i-го поставщика j-му потребителю. Система ограничений задачи не отличается от системы ограничений обычной транспортной задачи. Пусть X=(x_ij), i=1, 2, …, m, j=1, 2, …, n – некоторое опорное решение задачи. Запишем целевую функцию задачи. Обозначим через T(X) наибольшее значение элементов матрицы T=(t_ij), i=1, 2, …, m, j=1, 2, …, n, соответствующих клеткам таблицы, занятым опорным решением: T(X)= . Таким образом, за время T(X) план перевозок будет выполнен полностью. Математическая модель имеет вид:

T(X)= →min, (5.4.1.)

, i=1, 2, …, m, (5.4.2)

, j=1, 2, …, n, (5.4. 3.)

x_ij≥0, i=1, 2, …, m, j=1, 2, …, n. (5.4.4.)

Задача решается в следующем порядке. Находится начальное опорное решение X₁. Определяется значение целевой функции T(X₁)= = . Все свободные клетки, которым соответствуют значения t_ij>T(X₁), исключаются из рассмотрения (перечеркиваются). Занимать эти клетки нецелесообразно, так как повысится значение целевой функции. Чтобы понизить ее значение, необходимо освободить клетку (l₁, k₁), в которой t_ij достигает максимума. Для этого строят так называемые разгрузочные циклы, которые могут включать в свой состав несколько свободных клеток. В каждом разгрузочном цикле, начиная с разгружаемой клетки (l₁, k₁), расставляются поочередно знаки «—» и «+» и осуществляется сдвиг на величину 0=max{x_ij}. Если удается эту клетку разгрузить, то она исключается из рассмотрения (зачеркивается). Получается новое опорное решение X₂, на котором значение целевой функции меньше, чем на X₁. Далее снова пытаются разгрузить клетку, соответствующую T(X₂)= = . Процесс продолжается до тех пор, пока возможность разгрузить соответствующую клетку не исчезнет.

Пример. Найти минимальное время на осуществление всех перевозок для задачи, исходные данные которой приведены в табл. 5.4.1.

Таблица 5.4.1

bj ai
		8 - 30		+
		+		- 10

Таблица 5.4.2

bj ai
	10 - 20	+
	+	20 -

Р е ш е н и е. Составим начальное опорное решение X₁ по методу северо-западного угла (см. табл. 5.4.1). Базисные нули не записываем. Максимум целевой функции T(X₁)= =12 достигается в клетке (3, 4). Перечеркнем клетку (4, 1), в которой время доставки груза t₄₁= 15 больше T(X₁)=12.

Для улучшения решения разгрузим клетку (3, 4) с помощью цикла (3, 4), (2, 4), (2, 2), (3, 2). Обозначим цикл, найдем 0=min{10, 30}=10. Осуществив сдвиг по циклу, получим второе опорное решение X₂ (табл. 5.4.2). Максимум целевой функции на этом опорном решении T(X₂)= =10 достигается в клетке (1, 1). Перечеркнем клетку (3, 4), так как время t₃₄=12 больше, чем T(X₂)=10. Разгрузим клетку (1, 1) с помощью цикла (1, 1), (1, 2), (2, 2), (2, 1). Означим цикл, найдем 0=min{20, 20}=20. Осуществив сдвиг по циклу, получим третье опорное решение X₃ (табл. 5.4.3)

Таблица 5.4.3

bj ai
		20 -	+
		+ 4	- 5

Таблица 5.4.4

bj ai

Максимум целевой функции на этом опорном решении T(X₃)= {6,5,4,4,5,4,}=6 и достигается в клетке (1, 2). Перечеркнем клетки (1, 1), (2, 2), (2, 3) и (4, 3): в них время t₁₁=10, t₂₂=8, t₂₃=7 и t₄₃=9 больше, чем T(X₃)=6. Разгрузим клетку (1, 2) с помощью цикла (1, 2), (1, 3), (3, 3), (3, 2). Означим цикл, найдем 0=min {20,20}=20. Осуществив сдвиг по циклу, получим четвертое опорное решение X₄ (табл. 5.4.4). Максимум целевой функции на этом опорном решении T(X₄)= { 5,4,4,5,4,}=5 и достигается в клетках (2, 1) и (3, 3). Перечеркнем клетки (1, 2) и (4, 2), в которых время перевозок не менее t₂₁=5. С помощью оставшихся невычеркнутых клеток разгрузить клетки (2, 1) и (3, 3) не удается, поэтому X₄ является оптимальным решением.

Ответ: min T(X)=5 при X*= •

СПИСОК ЛИТЕРАТУРЫ.

1. Ермаков В.И. Общий курс высшей математики для экономистов: Учебник для экон. спец. вузов / Под ред. В.И. Ермакова. М.: ИНФРА-М., 1999.656 с.

2. Зайцев М.В. Прикладная математика: Сборник задач. Ч. 1. / М.В. Зайцев, А.А. Беляев. М.: Изд-во МГУК., 1999. 32 с.

3. Зайцев М.В. Прикладная математика: Сборник задач. Ч. 2. / М.В. Зайцев, А.А. Беляев. М.: Изд-во МГУК., 1999. 39 с.

4. Плотникова С.В. Математика в экономике: Метод. разработки и контр. задания / С.В. Плотникова. Тамбов: Изд-во Тамб. гос. техн. Ун-та, 1997. 52 с.

5. Матвеев В.И. Курс линейного программирования: Учеб. пособие / В.И. Матвеев, Р.В. Сачитов, В.Г. Шершнев. М: Изд-во «Менеджер», 1998. 102 с.