Поверхности, образованные вращением прямой линии

Точка на прямой линии.

Взаимное положение прямых линий.

Проекции плоскостей.

Задание многогранников на комплексном чертеже Монжа.

Поверхности.

1. Взаимное положение точки и прямой

т.А лежит на прямой т.В не лежит (III четверть) т.С выше прямой т.D перед прямой

Если точка лежит на прямой, то её проекции лежат на одноимённых проекциях прямой.

2. Взаимное положение двух прямых

2 прямые в пространстве могут быть:

а) //,

б) пересекаться,

в) скрещиваться.

Если две прямые //, то их одноимённые проекции также //^-ы друг другу.

Если две прямые пересекаются:

Одноимённые проекции двух пересекающихся прямых пересекаются и точки их пересечения лежат на одной линии связи. В противном случае прямые скрещиваются.

3. Проекции плоскостей. Способы задания и изображения плоскости на комплексном чертеже

Определителем плоскости называется совокупность геометрических элементов, однозначно задающих положение плоскости в пространстве.

На комплексном чертеже плоскость задаётся проекциями элементов своего определителя.

Способы задания плоскостей:

1) тремя точками, не лежащими на одной прямой

2) прямой и точкой, не лежащей на этой прямой

3) двумя пересекающимися прямыми

4) двумя параллельными прямыми

5) любой плоской фигурой

Мы рассмотрим способы задания плоскости общего положения.

Плоскость считается заданной, если относительно любой точки пространства можно однозначно решить задачу о её принадлежности к этой плоскости.

4. Плоскости частного положения

К плоскостям частного положения относятся // или ^ к какой-либо плоскости проекций.

Плоскость, ^ плоскости проекций, называется проецирующей плос костью.

^ к П₁ – горизонтально проецирующая,

^ к П₂ – фронтально проецирующая,

^ к П₃ – профильно проецирующая.

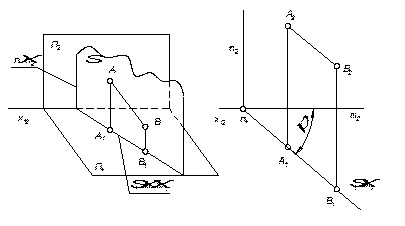
горизонтально-проецирующая

Горизонтальные проекции всех точек, линий и фигур, лежащих в плоскости, проецируются на горизонтальную проекцию плоскости – собирательное свойство плоскости.

фронтально-проецирующая

Плоскость, // плоскости проекций, называется плоскостью уровня.

// П₁ – горизонтальная плоскость уровня,

// П₂ – фронтальная плоскость уровня,

// П₃ – профильная плоскость уровня.

5. Точка в плоскости

Точка лежит в плоскости, если она принадлежит прямой, лежащей в этой плоскости.

6. Линии в плоскости

Среди множества прямых, лежащих в плоскости общего положения, можно выделить прямые частного положения.

Через любую точку плоскости общего положения всегда проходит 1 горизонталь, фронталь и профильная прямая уровня.

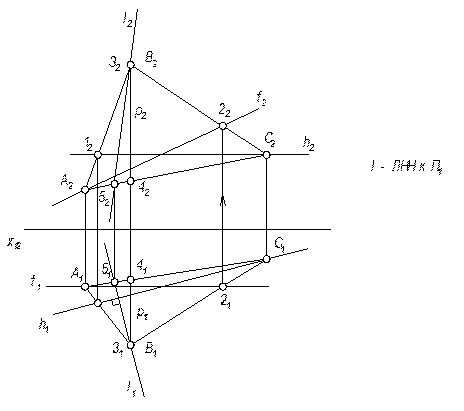
7. Параллельность прямой и плоскости

Прямая // плоскости, если в плоскости можно провести прямую, // данной.

1) Чаще всего приходится отвечать на вопрос: параллельны ли между собой заданная плоскость и прямая. Для этого на одной проекции плоскости проводится проекция прямой // проекции заданной прямой. Затем, из условия принадлежности прямой плоскости строится её вторая проекция и определяется, параллельна ли она второй проекции заданной прямой.

1) 2) не m не и l не АВС

2) построить прямую, // данной плоскости

например, Задача имеет решений

1) через заданную точку провести плоскость // данной прямой

1) m||l Q(m,n)||l

8. Параллельность плоскостей

Плоскости параллельны друг другу, если 2 пересекающиеся прямые одной плоскости //-ы двум пересекающимся прямым другой плоскости.

1) через заданную точку провести плоскость // данной.

2) заданы 2 плоскости, надо определить параллельны ли они между собой.

9. Классификация многогранников

Многогранником называется тело, ограниченное плоскими многоугольниками.

Многогранник называется выпуклым, если весь он лежит по одну сторону от плоскости любой его грани.

Многогранник называется правильным, если его боковые грани являются правильными многоугольниками.

Платон открыл 5 правильных выпуклых многогранников:

1) тетраэдр (четырёхгранник) – правильная треугольная пирамида;

2) гексаэдр (куб) – 8 вершин, 6 граней – квадратов;

3) октаэдр (8^ми-гранник) – 6 вершин, 8 граней – треугольников;

4) икосаэдр (20^ти-гранник) – 12 вершин, 20 граней – треугольников;

5) додекаэдр (12^ти-гранник) – 20 вершин, 12 граней – пятиугольников.

Среди неправильных многогранников наибольший интерес представляют:

1) призмы – боковые рёбра // друг другу, а боковыми гранями являются параллелограммы;

2) пирамиды - боковые рёбра пересекаются в одной точке вершины;

3) призматоиды – многогранники, ограниченные какими-либо двумя многоугольниками, расположенными в //^-ных плоскостях, называемыми основаниями, и треугольниками или трапециями, вершинами которых служат вершины оснований.

10. Изображение многогранников на комплексном чертеже

Многогранник на комплексном чертеже изображается проекциями своих вершин и рёбер.

Для придания однозначности чертежу вершины необходимо пронумеровать, а рёбра обвести с учётом видимости. Для определения видимости рёбер надо воспользоваться конкурирующими точками.

11. Понятие о поверхности

В математике под поверхностью понимается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая в декартовой системе координат уравнением вида F(x,y,z)=0.

Используя понятия «множество» и «точка» можно дать следующее определение: поверхностью называется непрерывное двухпараметрическое множество точек.

12. Способы задания поверхностей

Поверхность считается заданной, если относительно произвольной точки пространства можно однозначно решить вопрос о её принадлежности данной поверхности.

Для поверхности, заданной на чертеже, это условие становится следующим: поверхность считается заданной, если по одной проекции точки, принадлежащей поверхности, можно построить вторую проекцию точки.

Совокупность условий, необходимых для задания поверхности, называется определителем поверхности. Он состоит из геометрической и алгоритмической частей.

Геометрическая часть определителя – перечень геометрических элементов и фигур, которые участвуют в образовании поверхности.

Алгоритмическая часть определителя описывает взаимосвязи между элементами и фигурами, входящими в геометрическую часть, а также составляет совокупность правил, по которым образуется поверхность.

Иногда вместо алгоритмической части задаются параметры поверхности, которые делятся на параметры формы и параметры положения.

Существуют следующие способы задания поверхности:

1) аналитический – поверхность рассматривается как ГМТ, координаты которых удовлетворяют уравнению заданного вида:

F(x,y,z)=0

z=f(x,y)

- параметрическое задание

Главный недостаток – не наглядность,

Достоинство – удобно использовать для моделирования поверхностей на ЭВМ.

2) графический – поверхность задаётся на чертеже проекциями элементов своего определителя и некоторыми наиболее характерными линиями (типа очерк поверхности).

Очерк поверхности – линия, отделяющая проекции поверхности от остальной части плоскости проекций.

3) графоаналитический – часть линий аналитически, часть – графически: например, образующая - графически, направляющая – аналитически (линии – параметроносители).

13. Классификация поверхностей

Поверхности классифицируются по двум признакам:

1) по виду образующей линии

2 класса:

а) линейчатые – образующая - прямая;

б) не линейчатые – образующая – кривая;

2) по виду движения образующей линии:

а) поверхности плоскопараллельного переноса – образующая совершает поступательные движения;

б) поверхности вращения;

в) винтовые поверхности.

14. Поверхности вращения

Поверхностью вращения называется поверхность, образуемая при вращении некоторой линии вокруг неподвижной оси.

Каждая точка образующей при своём вращении будет описывать окружности, плоскости которых ^ к оси вращения. Такие окружности называются параллели. Самая большая параллель – экватор, самая маленькая – горло.

Если поверхность вращения рассекать плоскостями, проходящими через ось вращения, то в сечении будут лежать кривые, называемые меридианами. Все меридианы равны между собой, но меридиан, лежащий в плоскости уровня, называется главным.

Очерком поверхности вращения на одной плоскости проекций служит главный меридиан, а на другой – экватор и горло.

Чтобы построить точку, лежащую на поверхности вращения, нужно сначала взять вспомогательную линию на поверхности (лучше параллель) и расположить проекции точки на одноимённых проекциях вспомогательной линии.

Поверхности, образованные вращением прямой линии

1) цилиндр вращения – вращение прямой вокруг //-ой ей оси;

2) конус вращения – вращение прямой вокруг пересекающейся с ней оси;

3) однополосный гиперболоид вращения – вращение прямой вокруг скрещивающейся с ней оси.