Монотонность функции

Теорема 9.2.1. Достаточный признак монотонности функции. Пусть функция y=f(x) непрерывна и дифференцируема во всех точках отрезка [a;b]. Если:

а) всюду на этом отрезке f'(x)>0, функция f(x) возрастает на [a;b];

б) всюду на этом отрезке f'(x)<0, функция f(x) убывает на [a;b].

Доказательство.

а) Пусть при любых x С [a;b] f'(x)>0. Для любых x₁,x₂ C [a;b] запишем теорему Лагранжа: .

Если , то a <ξ<b. Пусть x₂ > x_{1 ,} то есть x₂ - x₁ >0 и f'(ξ)>0, тогда f(x₂)> f(x₁), то есть функция f(x) возрастает на отрезке [a;b].

б) доказательство аналогично.

Геометрическая интерпретация монотонности: 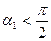, f(x) возрастает, , f(x) убывает (рис. 9.1)

Итак, если f'(x)>0, функция f(x) возрастает; f'(x)<0, функция f(x) убывает. Очевидно, интервалы монотонности определяются точками, в которых f'(x)=0. Назовем эти точки критическими или стационарными. Однако, не всякие стационарные точки разделяют интервалы монотонности (y=x³). Кроме того, интервалы монотонности, могут определяться точками, где производная не существует или функция терпит разрыв.

Рис. 9.1

Итак, при отыскании интервалов монотонности, следует найти критические точки, где f'(x)=0, точки, гдене существует производной (f'(x)=∞) и точки разрыва функции. Эти точки делят область определения функции на несколько интервалов, в каждом из которых производная не меняет знак.

Рис. 9.2

Примеры.

1. , x=0 – точка разрыва

2. y=x³-3x+2- всюду непрерывна и дифференцируема.

y'=3x²-3, x₁=-1, x₂=1 – критические точки.

, , .

В точке x=0 производная не существует.