Зеркальные антенны

Зеркальными называются антенны, у которых поле в раскрыве формируется за счет отражения электромагнитной волны, созданной первичным источником, от металлической поверхности специального рефлектора (зеркала). Первичный источник электромагнитной волны называется в этом случае облучателем.

Существует много разновидностей зеркальных антенн. Их можно классифицировать по количеству зеркал и по геометрии отражающей поверхности. По геометрии отражающей поверхности зеркальные антенны можно разделить на параболоиды вращения (рисунок 7.4, а), симметричные (рисунок 7.4, б,в) и несимметричные (рисунок 7.4, г) вырезки из них, параболические цилиндры (рисунок 7.4, д) и сферические зеркала (рисунок 7.4, е).

Помимо рассмотренных выше однозеркальных антенн, широкое распространение на практике получили двухзеркальные антенны. В этих антеннах для получения синфазного распределения поля в раскрыве используется две отражающие поверхности. Одна из них (большая) является основным зеркалом, которое чаще всего выполняется как параболоид вращения. Вторая (меньшая) может быть гиперболоидом (в частном случае плоскостью) или эллипсоидом. В первом случае (рисунок 7.5, а,б) антенну называют антенной Кассегрена, во втором (рисунок 7.5, в) – антенной Грегори. Эти названия, как и сами схемы антенн, заимствованы из оптики.

В антенне Кассегрена малое зеркало располагают так, чтобы один из фокусов гиперболы совпал с фокусом параболы . Во втором фокусе гиперболы () помещают облучатель. Исходящие из второго фокуса лучи после отражения от малого зеркала принимают такие направления, как будто они исходят из первого фокуса. Особенно наглядно это видно в случае плоского вспомогательного зеркала (рисунок 7.5, б).

В антенне Грегори с фокусом параболы совмещают один из фокусов эллипса. Во втором фокусе эллипса также помещают облучатель. Излученная волна после отражения от малого зеркала фокусируется в точке , которая играет роль фиктивного облучателя параболы.

В схеме Кассегрена малое зеркало помещают между параболой и ее фокусом, в то время как в схеме Грегори – за фокусом параболы. В связи с этим габаритный размер схемы Грегори больше и она используется реже.

Одно из основных преимуществ двухзеркальных антенн перед однозеркальными состоит в том, что наличие двух отражающих поверхностей предоставляет дополнительную степень свободы, которая может быть использована для регулировки амплитудного распределения в раскрыве, уменьшения фазовых ошибок при качании луча и т. п. В связи с этим КИП двухзеркальных антенн выше, чем у однозеркальных, и достигает 0.6–0.65.

Другое преимущество заключается в том, что облучатель может быть размещен вблизи вершины большого зеркала, за которым находятся передатчик и элементы фидерного тракта. При этом существенно сокращается длина волновода, идущего к облучателю. Это упрощает конструкцию фидерного тракта, улучшает согласование, уменьшает потери и шумовую температуру антенно-фидерного устройства.

Основная задача антенны – трансформировать сферическое поле облучателя в поле плоской волны. На рисунке 7.6 даны пояснения процесса преобразования волнового фронта в зеркальных антеннах. Здесь на рисунке 7.6, а показано преобразование волнового фронта при использовании одного зеркала, а на рисунке 7.6, б – двух зеркал. Рисунок 7.6, в поясняет трансформацию волнового поля в двухзеркальной антенне.

Профиль отражающего зеркала можно определить, исходя из условия, что электромагнитная волна, отраженная от рефлектора (зеркала), должна иметь плоский фазовый фронт. Это означает, как следует из рисунка 7.7, что оптическая длина пути между источником и плоским фронтом волны в раскрыве отражателя для любого луча должна быть одинакова.

Из анализа данного рисунка следует, что уравнение профиля зеркала будет определяться соотношением

. (7.24)

Выражение (7.24) является уравнением параболы в полярных координатах. Ось – ось параболы ‑ называется оптической осью зеркала.

В том, что парабола трансформирует сферический фронт волны в плоский, нетрудно убедиться, имея в виду, что параболой называется геометрическое место точек, равноудаленных от точки (фокуса) и прямой (директрисы).

Параболические антенны разделяются на длиннофокусные и короткофокусные. В длиннофокусной антенне фокус находится вне антенны, при этом (т.е. ). В короткофокусной антенне фокус находится внутри антенны, глубина зеркала (т.е. ).

Геометрия параболического зеркала, помимо глубины и фокусного расстояния , характеризуется также размером раскрыва и углом полураскрыва зеркала (см. рисунок 7.4). Найдем связь между , , и . С этой целью воспользуемся уравнением параболы в декартовой системе координат

. (7.25)

Подставив координаты крайней точки раскрыва и 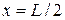в (7.25), получим

. (7.26)

Из находим

. (7.27)

Подставляя (7.27) в (7.24) при , получим

. (7.28а)

. (7.28б)

Формулы (7.11) и (7.13) позволяют по двум любым заданным геометрическим параметрам профиля зеркала найти два остальных.