Правила дифференцирования

1. ;

2. Производная суммы: пусть у=u(x)+ v (x)=u+ v,

Тогда

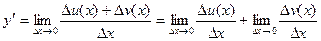
y'= u'+v' (если слагаемые дифференцируемые).

3. Производная произведения. (uv)'= u'v+uv'

Следствие 1. (С u)'=C· u'.

Следствие 2. (uvw)'= u'vw+uv'w+uvw'

4. Производная частного. .

Следствие: .

Производная сложной функции.

Пусть y=f(u), u= (x)- обе функции дифференцируемы,

у=f -сложная функция.

.

Производная обратной функции.

Пусть у= f(x)- непрерывная и однозначная функция.

Тогда х= (у)-обратная функции

Таблица производных основных элементарных функций.

1. y=sin u, u= (x), y'= cos u· ·u'

2. y=cos u, u= (x), y'=-sin u· ·u'

3. y=tg u, u= (x), y'= · u'

4.(ctg u)'=- ·u'

5. (arcsin 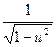u)'= · u'

6. (arcos 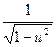u)'= - · u'

7. (arctg 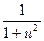u)'= · u'

8. (arcctg u)'=- 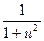· u'

9. y'= · u'

10. y'=

11. y= , y'=

y= u=

12. ,

13. , (p-любое действительное число)

Ln y=pln u,

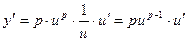
Следствия:

а) х'=1; б) в)

г) д)

Замечание. В некоторых случаях вместо непосредственного дифференцирования удобно провести логарифмическое дифференцирование.

Пример, .