Коэффициенты корреляции. Оценка тесноты связи

Точность коэффициентов регрессии. Построение доверительных интервалов и проверка гипотез относительно коэффициентов регрессии. Статистические критерии проверки значимости Прогноз. Доверитиельные интервалы для функции регрессии.

Оценка качества полученного уравнения регрессии основывается на методах дисперсионного анализа.

Наблюдаемые значения результативного признака можно представить в виде суммы двух составляющих и

. (13.1)

Величина представляет собой расчетное значение переменной у в наблюдении i. Остаток есть расхождение между наблюдаемым и расчетными значениями переменной у, или необъясненная с помощью уравнения регрессии часть переменной у.

Из (13.1) следует следующее соотношение между дисперсиями наблюдаемых значений переменной D(y), ее расчетных значений 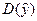и остатков D(е) (остаточной дисперсией D_ост = D(е))

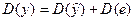(13.2)

Учитывая соотношения ,

и равенство (13.1) можно записать в виде

. (13.3)

Отношение объясненной части дисперсии переменной у ко всей дисперсии D(y)

или (13.4)

называют коэффициентом детерминации и используют для характеристики качества уравнения регрессии или соответствующей модели связи.

Соотношение (13.4) можно представить в альтернативном виде

или . (13.5)

Коэффициент детерминации принимает значения в диапазоне от нуля до единицы .

Коэффициент детерминации показывает, какая часть дисперсии результативного признака y объяснена уравнением регрессии.

Например, значение =0,56 говорит о том, что соответствующее уравнение регрессии объясняет 56 % дисперсии результативного признака.

Чем больше , тем большая часть дисперсии результативного признака y объясняется уравнением регрессии и тем лучше уравнение регрессии описывает исходные данные. При отсутствии зависимости между у и x коэффициент детерминации будет близок к нулю.

Таким образом, коэффициент детерминации может применяться для оценки качества (точности) уравнения регрессии.

Возникает вопрос, при каких значениях уравнение регрессии следует считать статистически незначимым, что делает необоснованным его использование в анализе. Ответ на этот вопрос дает F -критерий Фишера.

Введем следующие обозначения:

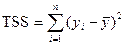- полная сумма квадратов отклонений;

- объясненная сумма квадратов отклонений;

- необъясненная сумма квадратов отклонений.

Известно, что величина

, (13.6)

где k - число независимых переменных в уравнении регрессии (для парной регрессии k = 1), в случае нормально распределенной ошибки 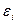является F -статистикой Фишера (случайная величина, распределенная по закону Фишера) с числом степеней свободы , .

Согласно F -критерию Фишера, выдвигается «нулевая» гипотеза 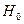о статистической незначимости уравнения регрессии (т. е. о статистически незначимом отличии величины F от нуля). Эта гипотеза отвергается при выполнении условия , где 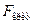определяется по таблицам F -критерия Фишера при числе степеней свободы и заданному уровню значимости α.

Определение 13.1. Уровнем значимости (обозначается α) в статистических гипотезах называется вероятность отвергнуть верную гипотезу (это, так называемая, ошибка первого рода).

Уровень значимости α обычно принимает значения 0,05 и 0,01, что соответствует вероятности совершения ошибки первого рода 5 % и 1 %.

Используя соотношение (13.6), величину F можно выразить через коэффициент детерминации

. (13.7)

Например, по данным 30 наблюдений было получено уравнение регрессии и =0,60

Необходимо проверить его значимость при уровне значимости α = 0,05.

Определим величину F -статистики, учитывая, что k = 1

По таблицам F -критерия Фишера при

и α = 0,05

находим 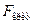= 4,20. Так как , то делаем вывод о статистической значимости уравнения регрессии.

Коэффициенты корреляции. Оценка тесноты связи.

Наряду с построением уравнения регрессии осуществляется оценка тесноты связи между явлениями (между переменными).

Тесноту связи в случае линейной зависимости характеризуют с помощью выборочного коэффициента корреляции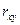

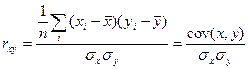(13.8)

или

. (13.9)

Здесь средние квадратические отклонения переменных x и y.

Выборочный коэффициент корреляции 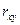связан с коэффициентом линейной регрессии b соотношением

. (13.10)

Выборочный коэффициент корреляции 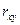принимает значения в диапазоне .

Чем ближе величина к единице, тем теснее линейная связь и тем лучше линейная зависимость согласуется с данными наблюдений. При = 1 связь становится функциональной, т. е. соотношение выполняется для всех наблюдений.

При 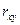> 0 связь является прямой, при 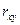< 0 – обратной.

Тесноту нелинейной связи (задаваемой уравнением нелинейной регрессии ) оценивают с помощью индекса корреляции R

. (13.11)

Индекс корреляции R принимает значения в диапазоне 0 ≤ R ≤ 1.

Чем ближе величина R к единице, тем теснее данная связь, тем лучше зависимость согласуется с данными наблюдений. При R = 1 ( = 1) связь становится функциональной, т. е. соотношение выполняется для всех наблюдений.

В случае линейной зависимости выборочный коэффициент корреляции 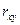и коэффициент детерминации связаны соотношением

(13.12)

Коэффициент детерминации может использоваться для оценки качества (точности) построенной модели регрессии. Чем выше этот показатель, тем лучше модель описывает исходные данные.