Крайний срок сдачи контрольных работ – две недели до начала сессии

Правило определения варианта: если последние две цифры номера зачетной книжки образуют число x Î (1; 30), то ваш вариант соответствует этому числу; если число x Î (31; 60), то ваш вариант x – 30; если число x Î 61; 90), то ваш вариант x – 60; если число x Î (91; 99], то ваш вариант x – 90; если x = 00, то ваш вариант 30.

Контрольное задание

по теории вероятностей и математической статистике

Задача 1

Дана функция распределения

Найти: а) плотность распределения вероятности 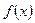; б) построить графики и 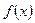; в) найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины ; г) найти вероятность попадания значений случайной величины в промежуток .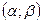

Задача 2

Известны математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины . Требуется: а) написать формулу плотности распределения вероятности; б) найти вероятность попадания этой величины в заданный интервал .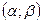

Задача 3

Найти с надежностью P доверительный интервал для оценки математического ожидания нормального распределения, зная выборочную среднюю , объем выборки и среднее квадратическое отклонение .

Задача 4

Методом наименьших квадратов найти зависимость вида 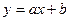между случайными величинами и , значения которых заданы таблицей:

X
Y

Данные для контрольного задания

№   Варианта	Задача1	Задача 2	Задача 3	Задача 4
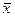
	a	b		a				n		P	y1	y2	y3	y4
	х2			(0,5;1)			(2;13)				0,95		3,4	3,8	5,1
	х3			(0,5;1)			(5;14)				0,94	0,2	1,1	1,8	3,3
				(1;1,5)			(4; 9)				0,93	0,1	1,2	1,9	3,4
	0,2х			(1; 3)			(3;10)				0,92		4,8	7,4	8,7
				(1; 2)			(2;11)				0,95	0,5	3,4	5,2	6,6
				(0,2;1)			(1;11)				0,94		6,3	7,8	9,7
	х4			(0,5;1)			(2;11)				0,93	1,2	2,6		7,4
	3х2 +2х			(0;03)			(3;10)				0,92	0,6		3,4	4,8
	0,5х-1			(2;3,5)			(4; 9)				0,94	5,4	6,6	9,2
				(1;2)			(6;10)				0,98	2,2	4,7	7,4
				(1;2)			(1; 4)				0,92	0,7		7,5	9,8
	sinx						(5;7)				0,95	0,1	2,8	6,4	8,8
	2sinx						(5; 10)				0,94	3,3	1,1	0,2	-2
	tgx			(0;0,4)			(2; 6)				0,93	3,9	2,7	3,2	1,1
	х2			(0; 0,3)			(2;13)				0,92	2,5	2,2	0,8	0,1
	х3			(0; 0,5)			(5;14)				0,95	2,2	5,7	9,8
	х4						(4; 9)				0,94	2,3	3,4	3,6	4,2
							(3; 10)				0,98	1,5	0,9	0,5	-0,3
	0,5х			(0,4; 1)			(2;11)				0,92	1,2	2,4	2,8	2,9
				(0,4; 1)			(1;12)				0,95	2,4	4,2	5,8	7,4
	2х-4			(2; 2,2)			(2;11)				0,93	3,4	5,2	6,8	8,4
	0.5х-1			(1; 3)			(3; 9)				0,92	4,4	6,2	7,8	9,4
				(0,5; 3)			(4; 9)				0,95	4,2	6,4	7,6	9,2
	0,25х2			(0,5; 2)			(6;10)				0,94	3,2	5,4	5,9	7,5
				(1; 2)			(2; 4)				0,95	1,2	2,5	1,7	2,2
	х-1						(7;10)				0,96	1,3	2,4	2,6	3,2
				(4; 5)			(4; 8)				0,98	2,9	1,7	2,3	0,1
				(6,5; 8)			(2; 6)				0,95	1,5		6,2
				(0,5; 2)			(1; 4)				0,92	-1	2,3	5,4
				(1; 3)			(2; 7)				0,95	3,3	5,6	8,1	4,3

Задача 5

1. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что студент знает: а) все три вопроса; б) только два вопроса; в) только один вопрос экзаменационного билета.

2. В каждой из двух урн находятся 5 белых и 10 черных шаров. Из первой урны переложили во вторую наудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется черным.

3. Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что: а) только один из стрелков попал в цель; б) только два стрелка попали в цель; в) все три стрелка попали в цель.

4. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 1600 испытаниях событие наступит 1200 раз.

5. Для сигнализации об аварии установлены три независимо работающие устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,9, второе – 0,95, третье – 0,85. Найти вероятность того, что при аварии сработает: а) только одно устройство; б) только два устройства; в) все три устройства.

6. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,02. Найти вероятность того, что при 150 испытаниях событие наступит 5 раз.

7. В партии из 1000 изделий имеются 10 дефектных. Найти вероятность того, что из 50 изделий, взятых наудачу из этой партии, ровно три окажутся дефектными.

8. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 125 испытаниях событие наступит не менее 75 и не более 90 раз.

9. На трех станках при одинаковых и независимых условиях изготовляются детали одного наименования. На первом станке изготовляют 10%, на втором – 30%, на третьем – 60% всех деталей. Вероятность каждой детали быть бездефектной равна 0,7, если она изготовлена на первом станке, 0,8 – на втором, и 0,9 – на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной.

10. Два брата входят в состав двух спортивных команд, состоящих из 12 человек каждая. В двух урнах имеются по 12 билетов с номерами от 1 до 12. Члены каждой команды вынимают наудачу по одному билету из определенной урны (без возвращения). Найти вероятность того, что оба брата вытащат билет номер 5.

11. Наудачу взяты два положительных числа х и у, каждое из которых не превышает двух. Найти вероятность того, что сумма х + у будет не больше трех, а частное х/y не больше двух.

12. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность.

13. Брошены три игральные кости. Найти вероятности следующих событий: а) на двух выпавших гранях появится одно очко, а на третьей грани – другое число очков; б) на двух выпавших гранях появится одинаковое число очков, а на третьей грани – другое число очков; в) на всех выпавших гранях появится разное число очков.

14. Среди 100 лотерейных билетов есть 5 выигрышных. Сколько надо приобрести билетов, чтобы вероятность выигрыша была не менее 0,5?

15. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг: а) квадрата; б) правильного треугольника; в) прямоугольного равнобедренного треугольника. Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга.

16. Двое бросают поочередно монету. Выигрывает тот, у кого первого выпадет герб. Какова вероятность, что будет произведено более четырех бросаний.

17. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

18. Число грузовых машин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:5. Вероятность, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.

19. Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятность попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,2; 0,3 и 0,4.

20. Две из четырех независимо работающих деталей прибора отказали. Найти вероятность того, что отказали первая и вторая детали, если вероятности отказа первой, второй, третьей и четвертой деталей соответственно равны 0,1; 0,2; 0,3 и 0,4.

21. Два равносильных противника играют в шахматы. Что вероятнее: а) выиграть одну партию из двух или две партии из четырех? б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаются.

22. а) Найти вероятность того, что событие А появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4.

б) событие В появится в случае, если событие А наступит не менее четырех раз. Найти вероятность наступления события В, если будет произведено пять независимых испытаний, в каждом из которых вероятность появления события А равна 0,8.

23. В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.

24. Отрезок разделен на четыре равные части. На отрезок на удачу брошено восемь точек. Найти вероятность того, что на каждую из четырех частей отрезка попадет по две точки. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

25. Вероятность появления события в каждом из независимых испытаний равна 0,3. Найти число испытаний n, при котором наивероятнейшее число появления события в этих испытаниях будет равно 30.

26. Подбрасывается три игральных кубика, подсчитывается сумма очков на верхних гранях. Что вероятнее – получить в сумме 9(событие А) или 10 (событие В) очков?

27. В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрывается 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчины?

28. В ящике 10 шаров, из которых 2 белых, 3 красных и 5 зеленых. Наудачу извлечены 3 шара. Найдите вероятность того, что все 3 шара разного цвета.

29. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают 3 изделия. Найдите вероятность того, что в полученной выборке одно изделие бракованное.

30. Из 10 билетов выигрышными являются два. Чему равна вероятность того, что среди взятых наудачу пяти билетов один выигрышный?

Основные теоремы и формулы теории вероятностей, используемые при решении контрольной работы

Основные теоремы и формулы теории вероятностей, используемые при решении контрольной работы и примеры решения некоторых задач

1.Теоремы сложения и умножения вероятностей.

1.1 Если события А и В несовместны, то вероятность суммы событий равна сумме вероятностей: р(А+В) = р(А)+р(В) (1).

1.2 Для совместных событий имеет место формула

р(А+В) = = р(А) + р(В) – р(АВ) (2),

где АВ – произведение событий.

1.3 Если события А и В независимы, то вероятность произведения событий равна произведению вероятностей событий:

р(АВ)=р(А)р(В) (3).

1.4 Для зависимых событий имеет место следующая формула:

р(АВ) = р(А)р(В/A) (4),

где р(В/А) – условная вероятность события В при условии А.

1.5 Формула полной вероятности p(A) = (5),

где H_i – гипотезы – события, одновременно с которыми может происходить событие А, причем АH₁+AH₂+…+AH_n = A.

1.6 Формула Байеса p(H_i/A) = (6).

2. Законы распределения случайных величин.

2.1 Биномиальный закон (формула Бернулли) Р_n(m)= p^m(1-p)^n-m (7) ,

где = - число сочетаний из n по m. При больших n имеет место формула Р_n(m) f(x) (8),

где f(x)= , x = (Локальная теорема Муавра-Лапласа).

2.2 Распределение Пуассона р(m) = (9).

При больших n (n>100) и малых р (р<0,3) формула Бернулли (5) может асимптотически представлена формулой (7): Р_n(m)» ,

где l=np (среднее число появления события).

2.3 Нормальное распределение f(x) = (10).

3. Основные числовые характеристики случайных величин.

3.1 Дискретные случайные величины:

Математическое ожидание М(Х) = = р₁х₁+ р₂х₂ + …+ р_nх_n=m, (11)

Дисперсия D(X) = = (x₁-m)²p₁+(x₂-m)²p₂+…+(x_n-m)²p_n (12)

где случайная величина Х задана законом распределения

х₁ х₂ …х_n

p₁ p₂… p_n

3.2 Непрерывные случайные величины:

Математическое ожидание М(Х) = (13),

где f(x) – плотность распределения случайной величины Х.

Дисперсия D(X) = 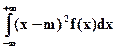(14),

где m – математическое ожидание, полученное по формуле (13).

Среднее квадратичное отклонение (стандартное отклонение)

s(Х) = (15).

4. Формула для оценки математического ожидания нормально распределен- ной случайной величины Х, имеющей дисперсию s(Х), объем выборки n,

(16)

Рассмотрим решение некоторых типовых задач.

Задача 1. Мастер обслуживает 5 станков. 10% рабочего времени он проводит у первого станка, 15% - у второго, 20% - у третьего, 25% - у четвертого и 30% - у пятого. Найти вероятность того, что в наудачу выбранный момент времени он находится 1) у первого или третьего станка; 2) у второго или пятого; 3) у первого или второго, или четвертого.

Решение. Обозначим через А, В, С, D, E – событие, состоящее в том, что в наудачу выбранный момент времени мастер находится у первого, второго, третьего, четвертого или пятого станка соответственно.

Из условия следует, что эти события попарно несовместны и р(А)=0,10, р(В)=0,15, р(С)=0,20, р(D)=0,25, р(E)=0,30. Принимая во внимание определение суммы событий и теорему о сложении вероятностей для несовместных событий (формула 1) находим:

P(A+C) = p(A) + p(C) = 0,10 +0,20 = 0,30;

P(B+E) = p(B) + p(E) = 0,15 +0,30 = 0,45;

P(A+B+D) = p(A) + p(B) + p(D) = 0,10 +0,15+0,25 = 0,50.

Задача 2. Сколько раз нужно подбросить две игральные кости (два игральных кубика), чтобы вероятность выпадения хотя бы один раз двух шестерок была бы больше?

Решение. Пусть событие А_i – “Выпадение двух шестерок при i-том подбрасывании”. Так как с каждой из 6 граней первого кубика может выпасть любая из 6 граней второго кубика, то всего исходов 6×6=36. И только один из них – благоприятный. Следовательно р(А_i)=1/36. Откуда q = 1- p = 1- 1/36 =35/36. То есть вероятность противоположного события В_i ”Не выпадут две шестерки” q = 35/36. А тогда вероятность того, что в n подбрасываниях не будет ни разу двух шестерок равна (35/36)ⁿ,

а вероятность противоположного события “выпадет хотя бы один раз пара шестерок” находится по формуле 1-(35/36)ⁿ и по условию это должно быть больше ½, другими словами 1-(35/36)ⁿ < ½, откуда (35/36)ⁿ > ½,

или n×ln(35/36) < ln(1/2), т.е. n > ln2/(ln35-ln36)» 0,6931/0,0284» 24,4. Итак, для того, чтобы вероятность выпадения двух шестерок была больше?, нужно подбросить кубик не менее 25 раз.

Задача 3. Вероятность появления события в каждом из n независимых испытаний равна 0,7. Найти вероятность того, что событие наступит 1500 раз в 2100 испытаниях.

Решение. По условию n = 2100, m = 1500, р = 0,7, q = 1-p = 1- 0,7 = 0,3. Так как n = 2100 достаточно большое число, воспользуемся локальной теоремой Муавра-Лапласа (8). Для этого вычислим

х = (m-np)/ = (1500-2100×0,7)/ = 30/21» 1,43.

По таблице функции f(x) находим f(1,43)» 0,1435. Искомая вероятность р₂₁₀₀(1500)» 1/ × f(1,43)» 0,0476×0,1435» 0,007.

Задача 4. Устройство состоит из 1000 элементов, работающих независимо. Вероятность отказа любого элемента в течение времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

Решение. По условию n = 1000, p = 0,002, m = 3. Поскольку число n велико, а вероятность р мала и элементы работают независимо, воспользуемся формулой Пуассона (9). Для этого найдем l: l = np =1000×0,002 = 2.

Искомая вероятность р₁₀₀₀(3)= 2³×е^-2/3! = 8×0,1353/6» 0,18.

Задача 5. Случайная величина задана функцией распределения:

Найти плотность распределения вероятностей, математическое ожидание, дисперсию и вероятность попадания случайной величины в интервал (1/4; 1).

Решение. Найдем плотность распределения вероятностей f(x). Для этого продифференцируем по х интегральную функцию распределения F(x):

f(x) = F^¢(x) =

Математическое ожидание М(Х) для непрерывной случайной величины находится по формуле (13) М(Х) = , а так как f(x) вне интервала (0;2] принимает значение ноль, то М(Х) = 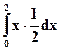= = 1.

По определению дисперсия D(Х) = , последнее выражение можно вычислить в виде разности М(Х²) – М²(Х), то есть

D(X) = = .

Вероятность попадания значений случайной величины X в интервал (1/4; 1] равна определенному интегралу в пределах от 1/4 до 1 от функции плотности распределения вероятнотей:

P(1/4<X<1) = .

Задача 6. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной следующим законом распределения:

X
p	0,2	0,8

Решение. Найдем искомое математическое ожидание:

М(Х) = х₁р₁ + х₂р₂ = 1×0,2+2×0,8 = 1,8.

Напишем закон распределения случайной величины Х²:

Х² 1² 2²

р 0,2 0,8

Найдем математическое ожидание М(Х²) = = 1×0,2+4×0,8 = 3,4.

Найдем искомую дисперсию D(X) = М(Х²) – М²(Х) = 3,4 – 1,8² = 0,16.

Вычислим среднее квадратичное отклонение:

s(X) = = = 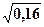0,4.

Задача 9. Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 0,95, зная выборочную среднюю =10,43(статистическую среднюю m_x), объем выборки (число наблюдений) n и среднее квадратическое отклонение =5.

Решение. Воспользуемся формулой (16) . Подставляя данные, получаем 10,43 – 1,96×(5/10)<a<10,43 + 1,96×(5/10), или окончательно 9,45 < a < 11,41.

Практическое задание

1) Подсчитать число появления буквы z в каждой их 32 строк указанных четырех строф поэмы А.С.Пушкина «Домик в Коломне» и составить статистический ряд (выборку) из 32 чисел;

2) Составить вариационный ряд, соответствующий полученному статистическому ряду;

3) Составить таблицу частот;

4) Построить полигон частот:

5) Вычислить выборочную среднюю;

6) Вычислить смещенную оценку дисперсии;

7) Вычислить несмещенную оценку дисперсии.

Данные по вариантам