The geometric interpretation of complex numbers

The study of complex numbers is greatly facilitated by interpreting then geometrically. Insofar as a complex number is defined as a pair of real numbers, it is natural to depict the complex number z=a+b as a point in the x, у - plane with Cartesian coordinates x=a and у=b, the number z = 0 corresponding to the origin of the plane. We shall call it the complex plane; the axis of abscissae is the real axis, the axis of ordinates is the imaginary axis of the complex plane. Thus we establish a one-to-one correspondence between the set of all complex numbers and the set of points of the complex plane, and also between the set of all complex numbers z=a+ib and the set of free vectors.

There is another extremely important form of representing complex numbers. It is possible to define the position of a point in the plane by means of polar coordinates (ρ, φ), where ρ is the distance of the point from the coordinate origin, and φ is the angle which the radius vector of the given point makes with the positive direction of the axis of abscissae. The positive direction of the variation of the angle φ is the counterclockwise direction (- 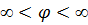). We get the so-called trigonometric form (or polar form) of a complex number: z =ρ(соs + i sin ).

Here, ρ is usually called the modulus (or absolute value) and the argument of the complex number and =|z|, φ =Arg z. These formulae express the real and imaginary parts of the complex number in terms of its modulus and argument. It is easy to express the modulus and argument of a complex number in terms of its real and imaginary parts. The argument of the complex number x= 0 is not defined and its modulus is zero. Two nonzero complex numbers are equal if and only if their moduli are equal and the values of their arguments are either equal or differ by a multiple of 2 .