 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Аналитическая геометрия. Прямая линия на плоскости
|
|
Задача 1.
Вычислить определитель.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
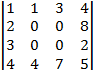
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
Задача 2.
Найти матрицу C, если
1. 
2. 
3. 
4. 
5. 
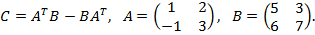
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
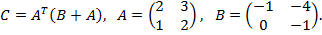
18. 
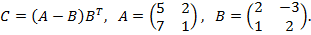
19. 
20. 
21. 
22. 
23. 
24. 
25. 
Задача 3.
Решить систему матричным методом.
1. 
2. 
3. 
4. 
5. 
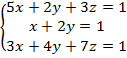
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
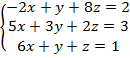
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
Задача 4.
Решить матричное уравнение.
1. 
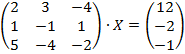
2. Даны матрица A= 
B= 
. Решить уравнения AX=B и YA=B.
3. y 
4. 
5. 
6. 
7. 
8. 
= 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
= 
23. 
24. 
25. 
Задача 5.
Коллинеарны ли векторы 
и 
, построенные по векторам a и b?
1. 
2. 
, 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
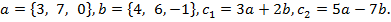
21. 
22. 
23. 
24. 
25. 
26. 
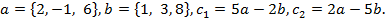
27. 
28. 
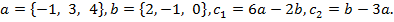
29. 
30. 
31. 
Задача 6.
Вычислить объём тетраэдра с вершинами в точках 
, 
, 
, 
и его высоту, опущенную из вершины на грань 
.
1. (1, 3, 6), (2, 2, 1), (-1, 6, -3), (-4, 6, -3).
2. (-4, 2, 6), (2, -3, 0), (-1-, 5, 8), (-5, 2, -4).
3. (7, 2, 4), (7, -1, -2), (3, 3, 1), (-4, 2, -1).
4. (2, 1, 4), (-1, 5, -2), (-7, -3, 2), (-6, -3, 6).
5. (0, -1, -1), (-2, 3, 5), (1, -5, -9), (-1, -6, -3).
6. (-1, -5, 2), (-6, 0, -3), (3, 6, -3), (-10, 6, 7).
7. (5, 2, 0), (2, 5, 0), (1, 2, 4), (-1, 1, 1).
8. (2, -1, -2), (1, 2, 1), (5, 0, -6), (-10, 9, -7).
9. (-2, 0, -4), (-1, 7, 1), (4, -8, -4), (1, -4, 6).
10. (14, 4, 5), (-5, -3, 2), (-2, -6, -3), (-2, 2, -1).
11. (1, 2, 0), (3, 0, -3), (5, 2, 6), (8, 4, -9).
12. (2, -1, 2), (1, 2, -1), (3, 2, 1), (-4, 2, 5).
13. (1, 1, 2), (-1, 1, 3), (2, -2, 4), (-1, 0, -2).
14. (2, 3, 1), (4, 1, -2), (6, 3, 7), (7, 5, -3).
15. (1, 1, -1), (2, 3, 1), (3, 2, 1), (5, 9, -8).
16. (1, 5, -7), (-3, 6, 3), (-2, 7, 3), (-4, 8, -12).
17. (-3, 4, -7), (1, 5, -4), (-5, -2, 0), (2, 5, 4).
18. (-1, 2, 6-3), (4, -1, 0), (2, 1, -2), (3, 4, 5).
19. (4, -1, 3), (-2, 1, 0), (0, -5, 1), (3, 2, -6).
20. (1, -1, 1), (-2, 0, 3), (2, 1, -1), (2, -2, -4).
21. (1, 2, 0), (1, -1, 2), (0, 1, -1), (-3, 0, 1).
22. (1, 0, 2), (1, 2, -1), (-2, -1, 6), (2, 1, 0).
23. (1, 2, -3), (1, 0, 1), (-2, -1, 6), (0, -5, -4).
24. (3, 10, -1), (-2, 3, -5), (-6, 0, -3), (1, -1, 2).
25. (-1, 2, 4), (-1, -2, -4), (3, 0, -1), (7, -3, 1).
26. (0, -3, 1), (-4, 1, 2), (2,-1, 5), (3, 1, -4).
27. (1, 3, 0), (4, -1, 2), (3, 0, 1), (-4, 3, 5).
28. (-2, -1, -1), (0, 3, 2), (3, 1, -4), (-4, 7, 3).
29. (-3, -5, 6), (2, 1, -4), (0, -3, -1), (-5, 2, -8).
30. (2, -4, -3), (5, 2-6, 0), (-1, 3, -3), (-10, -8, 7).
31. (1, -1, 2), (2, 1, 2), (1, 1, 4), (6, -3, 8).
Задача 7.
Аналитическая геометрия. Прямая линия на плоскости.
Дан треугольник с вершинами А(х1,у1),В(х2,у2),С(х3,у3).
Требуется найти 1.) Сравнения высоты и медианы, проведенные из вершины В;
2) угол между этими прямыми;
3) уравнение прямой, проходящей через вершину А, параллельно противоположной стороне; 4) длину высоты BD.
Координаты вершин треугольника даны в таблице.
| А | В | С | |
| (3;-2) | (1;2) | (-5;4) | |
| (2;4) | (-1;3) | (-2;-2) | |
| (1;0) | (-3;6) | (-1;-4) | |
| (2;2) | (-3;5) | (-2;8) | |
| (0;-4) | (1;3) | (2;-1) | |
| (3;-2) | (1;6) | (5;2) | |
| (0;1) | (-3;0) | (2;-3) | |
| (4;-3) | (2;1) | (0;-5) | |
| (-3;2) | (4;3) | (1;-2) | |
| (5;2) | (0;1) | (-1;3) | |
| (-2;-3) | (4;6) | (-4;1) | |
| (4-1) | (3;2) | (2;-5) | |
| (0;-4) | (3;7) | (6;4) | |
| (2;-3) | (1;1) | (-4;5) | |
| (6;-3) | (0;3) | (-2;3) | |
| (3;-6) | (4;2) | (1;4) | |
| (0;-1) | (5;1) | (2;5) | |
| (0;2) | (-3;7) | (-4;-4) | |
| (-4;-4) | (3;1) | (2;6) | |
| (5;3) | (0;-2) | (-l;l) | |
| (2;-4) | (1;5) | (-2;0) | |
| (6;-3) | (0;-5) | (2;5) | |
| (1;3) | (-4;-3) | (3;-5) | |
| (-3;4) | (4;1) | (1;-2) | |
| (2;6) | (-4;3) | (4;-4) | |
| (0;-7) | (2;1) | (5;-2 | |
| (2;-4) | (1;4) | (0;-2) | |
| (6;1) | (2;-5) | (0;3) | |
| (4;-3) | (5;6) | (0;1) | |
| (-5;-5) | (2:4) | (3;1) |
Задача 8.
Написать канонические уравнения прямой.
1. 
, 
.
2. 
, 
.
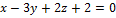3. 
, 
.
4. 
, 
.
5. 
, 
.
6. 
, 
.
7. 
, 
.
8. 
, 
.
9. 
, 
.
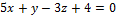10. 
, 
.
11. 
, 
.
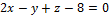12. 
, 
.
13. 
, 
.
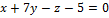14. 
, 
.
15. 
, 
.
16. 
, 
.
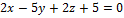17. , .
18. 
, 
.
19. 
, 
.
20. 
, 
.
21. 
, 
.
22. 
, 
.
23. 
, 
.
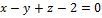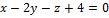24. 
, 
.
25. 
, 
.
Задача 9.
Найти точку пересечения прямой и плоскости.
1. 
, 
.
2. 
, 
.
3. 
, 
.
4. 
, 
.
5. 
, 
.
6. 
, 
.
7. 
, 
.
8. 
, 
.
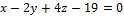9. 
, 
.
10. 
, 
.
11. 
, 
.
12. 
, 
.
13. 
, 
.
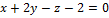14. 
, 
.
15. 
, 
.
16. 
, 
.
17. 
, 
.
18. 
, 
.
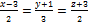19. , .
20. 
, 
.
21. 
, 
.
22. 
, 
.
23. 
, 
.
24. 
, 
.
25. 
, 
Дата публикования: 2015-10-09; Прочитано: 152 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
