Действия над матрицами

Суммой двух матриц А =(а_ij) _m,n и В =(b_ij) _m,n называется матрица С = А+В, элементы которой с_ij равны сумме соответствующих элементов а_ij и b_ij матриц А и В.

Например:

Для суммы матриц справедливы следующие свойства:

1. А+В = В+А — коммутативность;

2. А +(В+С)=(А+В)+ С — ассоциативность;

3. А+ 0 = А, 0 — нулевая матрица.

Произведением матрицы А= (а_ij) _m,n на число называется матрица В = А, элементы которой b_ij вычисляются следующим образом: b_ij = a_ij, i=1..m; j=1..n. Например, если то

Из определения произведения матрицы на число вытекают следующие свойства:

1. А=А 4.

2. 1· А =А 5.

3. 0 ·А = 0 6.

Определение: Матрица (- А) = (-1)· А называется противоположной матрице А.

Разность двух матриц одинакового размера определяется через предыдущие операции: A-B = A +(-1)· B.

Произведением матрицы А порядка m k на матрицу В порядка k n (т.е. количество столбцов первой матрицы равно числу строк второй) называется матрица С = А·В порядка m n, элементы которой с_ij вычисляются по формуле:

с_ij = a_i1b_1j + a_i2b_2j +... + a_ikb_ki, i =1.. m; j =1 ..n.

Из данного выражения следует правило умножения матриц: чтобы получить элемент, стоящий на пересечении i -й строки и j -го столбца матрицы С, необходимо все элементы i -й строки матрицы А умножить на соответствующие элементы j -го столбца матрицы В и полученные произведения сложить.

Для произведения матриц справедливы следующие свойства:

1. А (ВС) = (АВ) С 3. (А + В) С = АС + ВС

2. (АВ) = ( А) В 4. С (А + В) = СА + СВ

Произведение двух матриц не коммутативно, т.е. в общем случае АВ ВА. Если АВ = ВА, то матрицы А и В называются коммутативными. Так, например, единичная матрица Е коммутативна с любой квадратной матрицей того же порядка, причем АЕ = ЕА = А.

Пример 2.1. Найти произведения АВ и ВА матриц:

Решение:

Пример 2.2. Найти произведение AB двух векторов:

Решение. При умножении матрицы-строки на вектор-столбец получаем число :

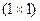Пример 2.3. Найти произведение KL следующих матриц:

Решение:

Транспонирование матрицы — это такое преобразование, при котором строки заменяются соответствующими столбцами. Обозначение транспонированной матрицы: .

Транспонированная матрица обладает следующими свойствами:

1. (А `)` = A

2. (A + B)` = A ` + B `

3. (AB)` = B ` A `

Матрица А =(а_ij) _m,n называется симметрической, если она совпадает со своей транспонированной.

Квадратная матрица А ^-1 порядка n называется обратной к матрице А, если она удовлетворяет соотношению:

А ^-1 А = АА ^-1 = Е.

Обратную матрицу можно вычислить на основании следующих элементарных преобразований (преобразований Жордана-Гаусса) над строками матрицы:

1. умножение строки матрицы на любое число, отличное от нуля;

2. прибавление к одной строке матрицы другой строки, умноженной на любое число.

Для того, чтобы вычислить обратную матрицу для матрицы А, необходимо составить матрицу , затем с помощью элементарных преобразований преобразовать матрицу А к виду единичной матрицы Е, тогда на месте единичной матрицы получим матрицу А ^-1.

Пример 2.5. Вычислить обратную матрицу для матрицы A:

Решение. Составим матрицу В⁽⁰⁾ вида:

Элемент и первую строку, содержащую данный элемент, назовем направляющими. Осуществим элементарные преобразования, в результате которых первый столбец преобразуется в единичный, с единицей в первой строке. Для этого к второй и третьей строкам прибавим первую строку, соответственно умноженную на 1 и (-2). В результате данных преобразований получим матрицу:

В матрице В ⁽¹⁾ преобразуем второй столбец в единичный. В качестве направляющего элемента выберем элемент Так как направляющий элемент , то разделим вторую (направляющую) строку на 3. Затем к первой строке прибавим вторую, умноженную на -3. Получим матрицу

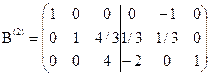
Третий столбец матрицы В ⁽²⁾ преобразуем в единичный. В качестве направляющего элемента выбираем Делим направляющую (третью) строку на 4 и ко второй строке прибавляем третью, умноженную на (–4/3). Получим матрицу

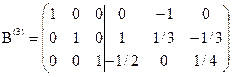
откуда

Выполним проверку:

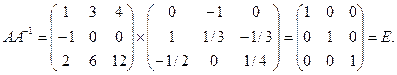
Аналогично A ^-1 A = E.