Трехточечная разностная схема. Метод прогонки

Из (4.3) – (4.4) получаем равенства

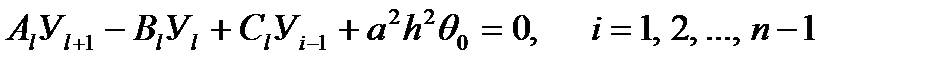(4.6)

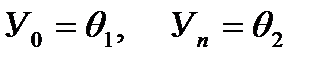
где

.

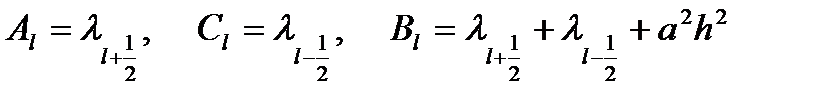(4.6) – называется трехточечной разностной схемой. Это есть система n-1 линейных алгебраических уравнений c неизвестными. Данная система имеет единственное решение.

Система (4.6) решается методом прогонки. Предполагаем, что решение (4.6) имеет вид

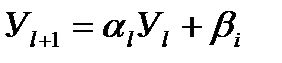(4.7)

Подставляем его в (4.6). Тогда,

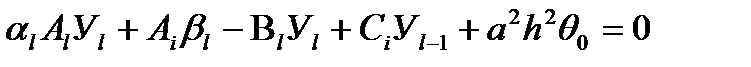
или

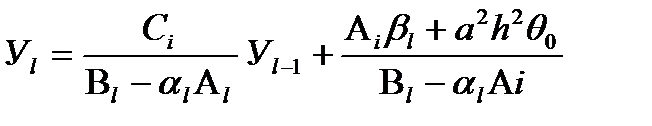(4.8)

Сравнивая (4.7) и (4.8) получим соотношения

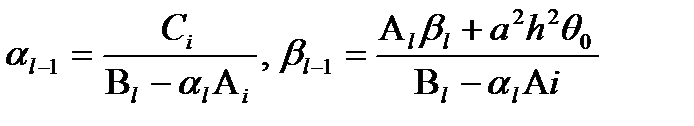(4.9)

Из (4.7) при l = n-1 получим

.

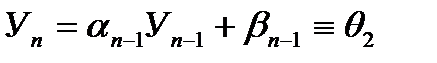Из этого тождества получим

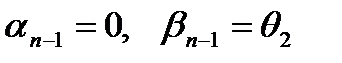. (4.10)

Из (4.9) и (4.10) определяются все

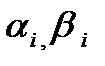i = n-2, n -3, …, 0.

После этого из (4.7) используя 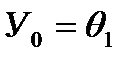определяются все

.

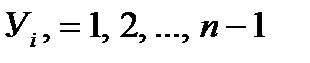Теорема 2. Есл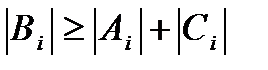и и 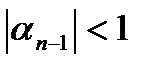, то метод прогонки является устойчивой. То есть, при реализаций схемы ошибки округления не накапливаются.

В нашем случае оба неравенства выполняются, поэтому метод прогонки является устойчивым.