Механизм образования производных величин и производных единиц

Положим, что исследуемая величина Q связана с величинами А, В, С,…, единицы которых предварительно установлены, следующим уравнением:

Q = F (A, B, C,…).

Входящие в уравнение величины можно представить в виде

Q = q[Q]; A = a[A]; B = b[B]; C = c[C]; …

где строчными буквами обозначены числовые значения, а буквами в квадратных скобках – единицы величин Q, А, В, С, …. Уменьшим единицы величин А, В, С, … в 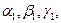… раз. Тогда числовое значение исследуемой величины Q увеличится в увеличится в ε число раз, зависящее от 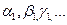, и будет составлять . Теперь снова уменьшим единицы исходных величин в 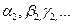раз. Тогда числовое значение 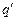увеличится в 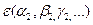раз, следовательно,

Но такое последовательное уменьшение единиц равносильно их одновременному уменьшению в 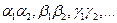раз. Поэтому

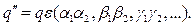
Сравним две последние формулы

.

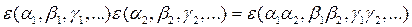Продифференцировав данное выражение по 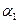и 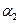получаем:

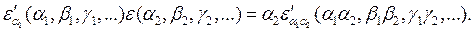
Разделим первое равенство на второе и сгруппируем в разных частях полученного выражения функции с одинаковыми индексами аргументов:

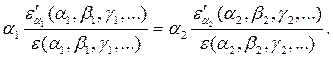
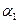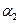Но так как числа и произвольны, то приходится сделать следующий вывод:

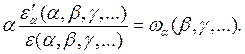
где - некоторая функция, не зависящая от α. Разделив переменные в данном дифференциальном уравнении, приведем его к виду

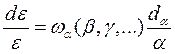
Интегрирование полученной формулы приводит к выражению

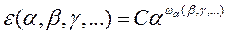
где С – постоянная интегрирования.

Дальнейшие рассуждения приводят нас к выражению:

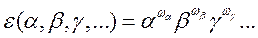
Полученное выражение называется формулой размерности, а его правая часть – размерностью (dimension) величины Q относительно величин А,В,С…. Последнее предложение обычно записывается в виде

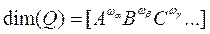
Если величины А, В, С, … являются основными, то формула размерности определяет размерность производной величины относительно основных величин. Размерности же основных величин выражаются через обозначения этих величин. Так, размерности длины, массы, времени, температуры записываются как

, , , .

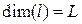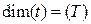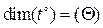Вычисление размерностей существенно упрощается, если принять во внимание два следующих очевидных правила:

1) если P = RQ, то dim (P) = dim (R) dim (Q );

2) если P = R/Q, то dim (P) = dim (R)/dim (Q ).

Пользуясь этими правилами, вычислим размерности некоторых величин:

размерность скорости 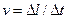составляет

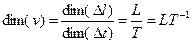
размерность ускорения находим из уравнения :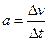

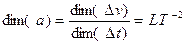
размерность силы определяется вторым законом Ньютона F = ma

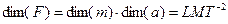
Вопрос №6