 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Сторонние силы – это силы неэлектростатического происхождения, способные поддерживать разность потенциалов на концах проводника
|
|
Понятие «сторонние силы» – это некоторая абстракция, которая обозначает силы разной природы, выполняющие одну и ту же функцию – преобразование различных видов энергии в энергию электрическую.
Главной задачей сторонних сил является генерация электрической энергии, то есть превращение энергии различной природы (механической, химической, тепловой, оптической и пр.) в электрическую. Эта задача решается путем перемещения электрически заряженных частиц против сил электростатического поля.
Если в проводнике создать электрическое поле и не принять мер для его поддержания, то, как было уже установлено, перемещение носителей заряда приведет очень быстро к тому, что поле внутри проводника исчезнет и, следовательно, ток прекратиться. Для того чтобы поддерживать ток достаточно долго, нужно от конца проводника с меньшим потенциалом (носители тока предполагаются положительными) непрерывно отводить приносимые сюда током заряды, а к концу с большим потенциалом непрерывно их подводить. Т.е. необходимо осуществить круговорот зарядов, при котором они двигались бы по замкнутому пути (рис. 4). Циркуляция вектора напряженности электростатического поля, как известно равна нулю. Поэтому в замкнутой цепи наряду с участками, на которых положительные заряды движутся в сторону убывания потенциала, должны иметься участки, на которых перенос положительных зарядов происходит в направлении возрастания потенциала  , т.е. против сил электростатического поля. Перемещение, зарядов на этих участках возможно лишь с помощью сил не электростатического происхождения, называемых сторонними силами. Таким образом, для поддержания тока необходимы сторонние силы, действующие либо на всем протяжении цепи, либо на отдельных ее участках.
, т.е. против сил электростатического поля. Перемещение, зарядов на этих участках возможно лишь с помощью сил не электростатического происхождения, называемых сторонними силами. Таким образом, для поддержания тока необходимы сторонние силы, действующие либо на всем протяжении цепи, либо на отдельных ее участках.
Природа сторонних сил может быть различной. Всякое устройство, в котором возникают сторонние силы, называется источником электрического тока. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля (рис. 4), благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
Сторонние силы можно охарактеризовать работой, которую они совершают над перемещающимися по цепи зарядами. Эта работа складывается из работы, совершаемой против электрического поля внутри источника тока  и работы, совершаемой против сил сопротивления среды
и работы, совершаемой против сил сопротивления среды  , т.е.
, т.е.  . Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы не потенциальные и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.
. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы не потенциальные и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.
1.5. Внутреннее сопротивление источника тока
В электрической цепи, состоящей из источника тока и проводников с электрическим сопротивлением  , электрический ток совершает работу не только на внешнем, но и на внутреннем участке цепи. Например, при подключении лампы накаливания к гальванической батарее карманного фонаря электрическим током нагреваются не только спираль лампы и подводящие провода, но и сама батарея. Электрическое сопротивление источника тока называется внутренним сопротивлением. В электромагнитном генераторе внутренним сопротивлением является электрическое сопротивление провода обмотки генератора. На внутреннем участке электрической цепи выделяется количество теплоты, равное:
, электрический ток совершает работу не только на внешнем, но и на внутреннем участке цепи. Например, при подключении лампы накаливания к гальванической батарее карманного фонаря электрическим током нагреваются не только спираль лампы и подводящие провода, но и сама батарея. Электрическое сопротивление источника тока называется внутренним сопротивлением. В электромагнитном генераторе внутренним сопротивлением является электрическое сопротивление провода обмотки генератора. На внутреннем участке электрической цепи выделяется количество теплоты, равное:
 ,
,
где  – внутреннее сопротивление источника тока. Полное количество теплоты, выделяющееся при протекании постоянного тока в замкнутой цепи, внешний и внутренний участки которой имеют сопротивления, соответственно равные
– внутреннее сопротивление источника тока. Полное количество теплоты, выделяющееся при протекании постоянного тока в замкнутой цепи, внешний и внутренний участки которой имеют сопротивления, соответственно равные  и
и  , равно:
, равно:
 .
.
1.6. Электродвижущая сила
Полная работа сил электростатического поля при движении зарядов по замкнутой цепи постоянного тока равна нулю. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток. При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Следовательно, вся работа электрического тока в замкнутой электрической цепи оказывается совершенной за счет действия сторонних сил, вызывающих разделение зарядов внутри источника и поддерживающих постоянное напряжение на выходе источника тока. Электродвижущая сила (ЭДС) – характеристика способности сторонних сил создавать большую или меньшую разность потенциалов на полюсах источника тока, величина скалярная.
Физическая величина, равная отношению работы  сторонних (не потенциальных) сил при перемещении положительного электрического заряда
сторонних (не потенциальных) сил при перемещении положительного электрического заряда  вдоль всей цепи (включая и источник тока) к величине этого заряда, называется электродвижущей силой источника (ЭДС):
вдоль всей цепи (включая и источник тока) к величине этого заряда, называется электродвижущей силой источника (ЭДС):
 .
.
Электродвижущая сила выражается в СИ тех же единицах, что и напряжение или разность потенциалов, т. е. в вольтах (В).
При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.
Стороннюю силу  , действующую на заряд, можно представить в виде:
, действующую на заряд, можно представить в виде:
 .
.
Векторную величину  называют напряженностью поля сторонних сил. Работу сторонних сил над зарядом
называют напряженностью поля сторонних сил. Работу сторонних сил над зарядом  на всём протяжении замкнутой цепи можно выразить следующим образом:
на всём протяжении замкнутой цепи можно выразить следующим образом:

Разделив эту работу на  , получим эдс, действующую в цепи:
, получим эдс, действующую в цепи:
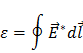
Таким образом, эдс, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил.
Последнее выражение дает самое общее определение ЭДС и пригодно для любых случаев. Если известно, какие силы вызывают движение зарядов в данном источнике, то всегда можно найти напряженность поля сторонних сил и вычислить ЭДС источника.
Для участка цепи электродвижущая сила, действующая на некотором участке 1 – 2, очевидно равна:
 .
.
Кроме сторонних сил на заряд действуют силы электростатического поля:
 .
.
Следовательно, результирующая сила, действующая в каждой точке цепи на заряд  , равна:
, равна:
 .
.
Работа, совершаемая этой силой над зарядом  на участке цепи 1 – 2, дается выражением:
на участке цепи 1 – 2, дается выражением:
 .
.
Для замкнутой цепи работа электростатических сил равна нулю, так что:
 .
.
Величина, численно равная работе, совершаемой электростатическими и сторонними силами при перемещении единичного положительного заряда, называется падением напряжения или просто напряжением  на данном участке цепи. Из уравнения:
на данном участке цепи. Из уравнения:  следует, что:
следует, что:
 .
.
При отсутствии сторонних сил напряжение  совпадает с разностью потенциалов:
совпадает с разностью потенциалов:
 .
.
Работа против сил электрического поля, по определению равна:
 .
.
Если полюсы источника разомкнуты, то  и тогда:
и тогда:
 ,
,
т.е. эдс источника тока при разомкнутой внешней цепи равна разности потенциалов, которая создается на его полюсах. Таким образом, размерность эдс совпадает с размерностью потенциала. Поэтому  измеряется в тех же единицах, что и
измеряется в тех же единицах, что и  – в вольтах.
– в вольтах.
 Рис. 7.
Рис. 7.
|
 ; если ток внутри источника идёт от «+» к «–» (рис. 7 б),
; если ток внутри источника идёт от «+» к «–» (рис. 7 б),  .
.Таким образом, ЭДС контура равна алгебраической сумме ЭДС каждого источника, а ЭДС источника равна разности потенциалов на его полюсах при разомкнутой внешней цепи.
Физическая природа электродвижущих сил в разных источниках различна.
 Рис. 8.
Рис. 8.
|
 . Диск включен в электрическую цепь при помощи скользящих контактов, касающихся оси диска и его окружности.
. Диск включен в электрическую цепь при помощи скользящих контактов, касающихся оси диска и его окружности.
Центростремительная сила  , где
, где  – масса электрона;
– масса электрона;  – расстояние от оси диска. Эта сила действует на электрон и поэтому
– расстояние от оси диска. Эта сила действует на электрон и поэтому  , возникающая ЭДС равна:
, возникающая ЭДС равна:
 .
.
1.7. Соединение источников тока
Источники тока соединить в батарею можно также двумя способами: параллельным и последовательным
Параллельное соединение источников тока
Параллельное соединение источников тока первым способом, показано на рис. 9.
При параллельном способе соединения источников тока соединяют между собой все положительные и все отрицательные полюсы. Напряжение на разомкнутой батарее будет равно напряжению на каждом отдельном источнике, т. е. при параллельном способе соединения ЭДС батареи равна ЭДС одного источника. Сопротивление батареи при параллельном включении источников будет меньше сопротивления одного элемента, потому что в этом случае их проводимости суммируются.
 Рис. 9. Параллельное соединение источников тока
Рис. 9. Параллельное соединение источников тока
|
При соединении
 источников тока с
источников тока с  и сопротивлениями
и сопротивлениями  параллельно одноименными полюсами, если
параллельно одноименными полюсами, если  , то:
, то:

 .
.
Последовательное соединение источников тока
 Рис. 10. Последовательное соединение источников тока
Рис. 10. Последовательное соединение источников тока
|
При последовательном соединении источников тока (рис. 10) два соседних источника соединяются между собой противоположными полюсами.
Разность потенциалов между положительным полюсом последнего источника и отрицательным полюсом первого будет равна сумме разностей потенциалов между полюсами каждого источника. Из этого вытекает, что при последовательном соединении ЭДС батареи равна сумме ЭДС источников, включенных в батарею. Общее сопротивление батареи при последовательном включении источников равняется сумме внутренних сопротивлений отдельных элементов.
При соединении  источников тока с
источников тока с  и сопротивлениями
и сопротивлениями  последовательно:
последовательно:

 .
.
Параллельное соединение источников тока применяют тогда, когда нужно получить источник тока с малым внутренним сопротивлением или когда для нормальной работы потребителя электроэнергии в цепи должен протекать ток больший, чем допустимый ток одного источника. Параллельное соединение выгодно, когда  невелико по сравнению с
невелико по сравнению с  . Иногда применяют смешанное соединение источников.
. Иногда применяют смешанное соединение источников.
 Рис. 11.
Рис. 11.
|
1.8. Напряжение на неоднородном участке цепи
Рассмотрим вначале однородный участок цепи (рис. 11, а). В этом случае работу по перемещению заряда совершают только силы стационарного электрического поля, и этот участок характеризуют разностью потенциалов  . Разность потенциалов на концах участка
. Разность потенциалов на концах участка  , где
, где  – работа сил стационарного электрического поля. Т.о., напряжение на концах участка цепи совпадает с разностью потенциалов только в случае, если на этом участке нет ЭДС, т.е. на однородном участке цепи
– работа сил стационарного электрического поля. Т.о., напряжение на концах участка цепи совпадает с разностью потенциалов только в случае, если на этом участке нет ЭДС, т.е. на однородном участке цепи 
 .
.
Уточним понятие напряжения для участка цепи. Напряженность  поля в любой точке неоднородного участка цепи равна векторной сумме поля кулоновских сил и поля сторонних сил, т.е.
поля в любой точке неоднородного участка цепи равна векторной сумме поля кулоновских сил и поля сторонних сил, т.е.
 .
.
Величина, численно равная работе по переносу единичного положительного заряда суммарным полем кулоновских и сторонних сил на участке цепи (1 – 2), называется напряжением на этом участке  .
.
Так как  , или
, или  , тогда
, тогда  .
.
В электротехнике часто используют термин падение напряжения – изменение напряжения вследствие переноса заряда через сопротивление:  .
.
Неоднородный участок цепи (рис. 9, б) содержит в отличие от однородного участка источник ЭДС, и к работе сил электростатического поля на этом участке добавляется работа сторонних сил:
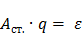 ,
,
где  – эдс источника тока этого участка цепи. По определению,
– эдс источника тока этого участка цепи. По определению,  , где
, где  – положительный заряд, который перемещается между любыми двумя точками цепи;
– положительный заряд, который перемещается между любыми двумя точками цепи;  – разность потенциалов точек в начале и конце рассматриваемого участка. Тогда напряжение
– разность потенциалов точек в начале и конце рассматриваемого участка. Тогда напряжение  на участке цепи представляет собой физическую скалярную величину, равную суммарной работе сторонних сил и сил электростатического поля по перемещению единичного положительного заряда на этом участке:
на участке цепи представляет собой физическую скалярную величину, равную суммарной работе сторонних сил и сил электростатического поля по перемещению единичного положительного заряда на этом участке:
 . (1)
. (1)
Из этой формулы видно, что в общем случае напряжение на неоднородном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке.
Если же на участке действуют только электрические силы  , то:
, то:
 .
.
Таким образом, только для однородного участка цепи понятия напряжения и разности потенциалов совпадают.
Закон Ома для неоднородного участка цепи
Из выражения (1) следует закон Ома для неоднородного участка цепи (обобщенный закон Ома для участка цепи содержащей источник ЭДС):
 , (2)
, (2)
где 
 общее сопротивление неоднородного участка.
общее сопротивление неоднородного участка.
Обобщенный закон Ома выражает закон сохранения энергии применительно к участку цепи постоянного тока. Он в равной мере справедлив как для пассивных участков (не содержащих ЭДС), так и для активных.
1.9. Закон Ома для замкнутой цепи
 Рис.12.
Рис.12.
|
 внутренней и внешней. Внутренняя часть цепи представляет собой источник тока, обладающий внутренним сопротивлением
внутренней и внешней. Внутренняя часть цепи представляет собой источник тока, обладающий внутренним сопротивлением  ; внешняя
; внешняя  различные потребители, соединительные провода, приборы и т.д. Общее сопротивление внешней части обозначается
различные потребители, соединительные провода, приборы и т.д. Общее сопротивление внешней части обозначается  . Тогда полное сопротивление цепи равно
. Тогда полное сопротивление цепи равно  .
.
Электрические носители во внешней цепи движутся от точки большего потенциала к точке меньшего потенциала. А так как ток  замкнут и представляет собой движение зарядов, которые нигде не накапливаются, то внутри источника тока заряды движутся от точки меньшего потенциала
замкнут и представляет собой движение зарядов, которые нигде не накапливаются, то внутри источника тока заряды движутся от точки меньшего потенциала  к точке большего потенциала
к точке большего потенциала  .
.
По закону Ома для внешнего (однородного) участка цепи имеем:
 .
.
Внутренний участок цепи является неоднородным. Согласно закону Ома для неоднородного участка цепи:
 .
.
Сложив эти равенства, получим:
 . (3)
. (3)
Из формулы (3) получаем:
 , (4)
, (4)
где: 
 ЭДС источника напряжения (В),
ЭДС источника напряжения (В),  сила тока в цепи (А),
сила тока в цепи (А),  сопротивление всех внешних элементов цепи (Ом),
сопротивление всех внешних элементов цепи (Ом), 
 внутреннее сопротивление источника напряжения (Ом).
внутреннее сопротивление источника напряжения (Ом).
Последняя формула (4) представляет собой закон Ома для замкнутой цепи постоянного тока:
Сила тока в цепи прямо пропорциональна ЭДС источника и обратно пропорциональна полному сопротивлению цепи.
Формулу (3) можно представить в виде:
 , (5)
, (5)
где 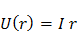 – напряжение на внутреннем участке цепи,
– напряжение на внутреннем участке цепи,  – напряжение во внешней цепи.
– напряжение во внешней цепи.
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника.
Из формулы (5) следует:
 . (6)
. (6)
Из формулы (6) видно, что напряжение на внешнем участке уменьшается с увеличением силы тока в цепи при  .
.
Подставим в формулу (6) силу тока (4), получим:
 . (7)
. (7)
Проанализируем выражение (7) для некоторых предельных режимов работы цепи.
 Рис. 13.
Рис. 13.
|
 ,
,  , т.е. напряжение на полюсах источника тока при разомкнутой цепи равно ЭДС источника тока.
, т.е. напряжение на полюсах источника тока при разомкнутой цепи равно ЭДС источника тока.
На этом основана возможность приблизительного измерения ЭДС источника тока с помощью вольтметра, сопротивление которого много больше внутреннего сопротивления источника тока  . Для этого вольтметр подключают к клеммам источника тока (рис. 13). То есть, в этом случае всегда
. Для этого вольтметр подключают к клеммам источника тока (рис. 13). То есть, в этом случае всегда  .
.
б) Если к клеммам источника тока подключить проводник, сопротивление которого  , то
, то  , тогда
, тогда  , а сила тока
, а сила тока  – достигает максимального значения.
– достигает максимального значения.
Подключение к полюсам источника тока проводника с ничтожно малым сопротивлением  называется коротким замыканием, а максимальную для данного источника силу тока называют током короткого замыкания:
называется коротким замыканием, а максимальную для данного источника силу тока называют током короткого замыкания:
 .
.
Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой  и внутренним сопротивлением
и внутренним сопротивлением  . У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов
. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов  , используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей. В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику подсоединяется некоторое внешнее балластное сопротивление.
, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей. В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику подсоединяется некоторое внешнее балластное сопротивление.
На рис.14 дано схематическое изображение источника постоянного тока с ЭДС равной  и внутренним сопротивлением
и внутренним сопротивлением  в трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к.з.). Указаны напряженность
в трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к.з.). Указаны напряженность  электрического поля внутри батареи и силы, действующие на положительные заряды:
электрического поля внутри батареи и силы, действующие на положительные заряды:  – электрическая сила и
– электрическая сила и  – сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.
– сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.
Работа и мощность постоянного электрического тока на однородном участке цепи.
Рассмотрим однородный участок цепи (рис. 11 а).
При протекании тока по однородному участку цепи электрическое поле совершает работу, называемую работой тока.
Работа тока – это работа электрического поля по переносу электрических зарядов вдоль проводника.
За время  по цепи протекает заряд
по цепи протекает заряд  . Электрическое поле на выделенном участке совершает работу:
. Электрическое поле на выделенном участке совершает работу:
 ,
,
где  – напряжение.
– напряжение.
 Рис. 14. Схематическое изображение источника постоянного тока:
1 – батарея разомкнута;
2 – батарея замкнута на внешнее сопротивление R;
3 – режим короткого замыкания.
Рис. 14. Схематическое изображение источника постоянного тока:
1 – батарея разомкнута;
2 – батарея замкнута на внешнее сопротивление R;
3 – режим короткого замыкания.
|
Это соотношение выражает закон сохранения энергии для однородного участка цепи: работа равна изменению энергии участка цепи, поэтому выделяемая проводником энергия равна работе тока.
Мощность электрического тока равна отношению работы тока  ко времени
ко времени  , за которое эта работа совершена:
, за которое эта работа совершена:
 .
.
Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт). Существует внесистемная единица работы тока:  .
.
1.10. Закон Джоуля – Ленца
Если на участке цепи под действием электрического поля не совершается механическая работа и не происходят химические превращения веществ, то работа электрического поля приводит только к нагреванию проводника. При этом работа электрического тока равна количеству теплоты, выделяемому проводником с током:
 . (8)
. (8)
Работа  электрического тока
электрического тока  , протекающего по неподвижному проводнику с сопротивлением
, протекающего по неподвижному проводнику с сопротивлением  , преобразуется в тепло
, преобразуется в тепло  , выделяющееся на проводнике.
, выделяющееся на проводнике.
Закон (8) был экспериментально установлен английским ученым Джеймсом Джоулем (1818 – 1889) и русским ученым Эмилием Христиановичем Ленцем (1804 – 1865), поэтому носит название закона Джоуля – Ленца.
1.11. Работа и мощность постоянного тока в замкнутой цепи
Рассмотрим теперь полную (замкнутую) цепь постоянного тока, состоящую из источника с электродвижущей силой  и внутренним сопротивлением
и внутренним сопротивлением  и внешнего однородного участка с сопротивлением
и внешнего однородного участка с сопротивлением  , т.е. неоднородный участок цепи (рис. 12). Закон Ома для замкнутой цепи записывается в виде:
, т.е. неоднородный участок цепи (рис. 12). Закон Ома для замкнутой цепи записывается в виде:
 .
.
Умножив обе части этой формулы на  , мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:
, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:

Первый член в левой части  – тепло, выделяющееся на внешнем участке цепи за время
– тепло, выделяющееся на внешнем участке цепи за время  , второй член
, второй член  – тепло, выделяющееся внутри источника за то же время.
– тепло, выделяющееся внутри источника за то же время.
Выражение  равно работе сторонних сил
равно работе сторонних сил  , действующих внутри источника.
, действующих внутри источника.
При протекании электрического тока по замкнутой цепи работа сторонних сил  преобразуется в тепло, выделяющееся во внешней цепи
преобразуется в тепло, выделяющееся во внешней цепи 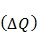 и внутри источника
и внутри источника  .
.
 .
.
Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами, действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными участками цепи.
Внешняя цепь может представлять собой не только проводник с сопротивлением  , но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под
, но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под  нужно понимать эквивалентное сопротивление нагрузки. Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, но и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.
нужно понимать эквивалентное сопротивление нагрузки. Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, но и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.
Рассмотрим также замкнутую электрическую цепь, с точки зрения развиваемой источником мощности. Как известно, мощность, выделяемая в виде тепла при прохождении электрического тока через сопротивление, определяется законом Джоуля–Ленца:
 . (9)
. (9)
Соотношение (9) определяет полезную мощность, развиваемую источником на внешнем сопротивлении  . Аналогичное соотношение, но с сопротивлением
. Аналогичное соотношение, но с сопротивлением 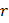 ;
;  – определяет мощность, выделяющуюся в виде тепла на внутреннее сопротивление источника.
– определяет мощность, выделяющуюся в виде тепла на внутреннее сопротивление источника.
С учетом закона Ома для участка цепи  полезную мощность можно найти, если известны любые две величины из трех:
полезную мощность можно найти, если известны любые две величины из трех: 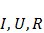 .
.
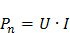 ,
,  ,
,  .
.
Полная мощность (т.е. работа, совершаемая сторонними силами за единицу времени) является суммой полезной мощности и мощности, выделяющейся на внутреннее сопротивление:
 (10)
(10)
Тогда полезная мощность может быть так же представлена в виде:

Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность  прибавляется к поглощаемой или вычитается из отдаваемой.
прибавляется к поглощаемой или вычитается из отдаваемой.
Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра и амперметра.
Для измерения коэффициента реактивной мощности применяют фазометры.
Государственный эталон – ГЭТ 153-2012 Государственный первичный эталон единицы электрической мощности в диапазоне частот от 1 до 2500 Гц. Институт-хранитель: ВНИИМ.
1.12. КПД источника тока
Коэффициент полезного действия (КПД) источника постоянного тока равен:
 . (11)
. (11)
Используя соотношения (10), (11) можно показать, что
 ;
;  ;
;  . (12)
. (12)
Полная мощность, развиваемая источником тока, достигает максимума в режиме короткого замыкания, т.е. при  . В этом случае вся тепловая мощность выделяется внутри источника тока на его внутренне сопротивление. С ростом внешнего сопротивления полная мощность уменьшается, асимптотически приближаясь к нулевому значению.
. В этом случае вся тепловая мощность выделяется внутри источника тока на его внутренне сопротивление. С ростом внешнего сопротивления полная мощность уменьшается, асимптотически приближаясь к нулевому значению.
Полезная мощность изменяется в зависимости от внешнего сопротивления более сложным образом. Действительно, из формулы (12) следует, что  при крайних значениях внешнего сопротивления: при
при крайних значениях внешнего сопротивления: при  и
и  . Таким образом, максимум полезной мощности должен приходиться на промежуточные значения внешнего сопротивления.
. Таким образом, максимум полезной мощности должен приходиться на промежуточные значения внешнего сопротивления.
Величину внешнего сопротивления, соответствующую максимуму полезной мощности, можно найти, используя метод дифференциального исчисления. Можно показать, что максимум полезной мощности соответствует 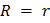 , т.е. равенству внешнего и внутреннего сопротивлений.
, т.е. равенству внешнего и внутреннего сопротивлений.
Чтобы убедиться в этом возьмем производную от  по внешнему сопротивлению
по внешнему сопротивлению  :
:
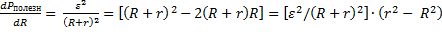 .
.
По условию максимума требуется 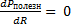 , откуда
, откуда  .
.
Определив знак второй производной, легко убедиться, что это действительно условие максимума.
В электротехнике режим максимальной полезной мощности называется режимом согласования источника тока с его нагрузкой.
На рис. 15 графически представлены зависимости мощности источника  (полной мощности), полезной мощности
(полной мощности), полезной мощности  , выделяемой во внешней цепи, и коэффициента полезного действия
, выделяемой во внешней цепи, и коэффициента полезного действия  от тока в цепи
от тока в цепи  для источника с ЭДС, равной
для источника с ЭДС, равной  , и внутренним сопротивлением
, и внутренним сопротивлением  . Ток в цепи может изменяться в пределах от
. Ток в цепи может изменяться в пределах от  (при
(при  ) до
) до  (при
(при  ).
).
Из приведенных графиков видно, что максимальная мощность во внешней цепи  , равная:
, равная:
 ,
,
достигается при  .
.
При этом ток в цепи:  ,
,
 Рис. 15.
Зависимость мощности источника
Рис. 15.
Зависимость мощности источника  ,
мощности во внешней цепи ,
мощности во внешней цепи 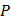 и КПД источника
и КПД источника  от силы тока. от силы тока.
|
а КПД источника равен
 . Максимальное значение КПД источника достигается при
. Максимальное значение КПД источника достигается при  , т.е. при
, т.е. при  . В случае короткого замыкания полезная мощность
. В случае короткого замыкания полезная мощность  и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль.
и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль. Дата публикования: 2015-10-09; Прочитано: 4985 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
