 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Задания для домашней контрольной работы
|
|
ЗАДАНИЕ 1 Найти неопределенный интеграл
| Вариант | Интеграл | Вариант | Интеграл |
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
| а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
| ||
а)  б)
б)  в)
в) 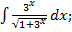 г)
г)  д)
д)  е)
е) 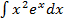
| а) 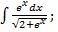 б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
| ||
а) 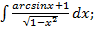 б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
| а)  б)
б)  в)
в) 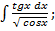 г)
г)  д)
д)  е)
е) 
| ||
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
| а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
| ||
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
| а)  б)
б)  в)
в)  г)
г)  д)
д) 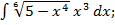 е)
е) 
|
ЗАДАНИЕ 2 Вычислить определенный интеграл
| Вариант | Интеграл | Вариант | Интеграл |
а)  б)
б)  в)
в) 
| а) 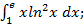 б)
б)  в)
в) 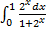
| ||
а)  б)
б)  в)
в) 
| а)  б)
б)  в)
в) 
| ||
а)  б)
б) 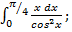 в)
в) 
| а)  б)
б)  в)
в) 
| ||
а)  б)
б)  в)
в) 
| а) 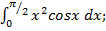 б)
б)  в)
в) 
| ||
а)  б)
б)  в)
в) 
| а)  б)
б)  в)
в) 
|
ЗАДАНИЕ 3 Вычислить площадь фигуры, ограниченной линиями
| Вариант | Уравнение линий | Вариант | Уравнение линий |
а)  ;
б) ;
б)  ;
в) ;
в) 
| а)  б)
б)  ;
в) ;
в) 
| ||
а)  ;
б) ;
б)  в)
в) 
| а)  ;
б) ;
б)  в)
в)  . .
| ||
а)  ;
б) ;
б)  ;
в) ;
в) 
| а)  ;
б) ;
б)  ;
в) ;
в) 
| ||
а)  ;
б) ;
б)  в) y=
в) y=  . .
| а)  ;
б) y= ;
б) y=  в)
в)  . .
| ||
а)  б) y=x+1, y=
б) y=x+1, y=  в)
в) 
| а)  б)
б)  ;
в) ;
в) 
|
ЗАДАНИЕ 4 Вычислить несобственный интеграл
| Вариант | Интеграл | Вариант | Интеграл |
а)  б)
б) 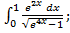 в)
в)  . .
| а) 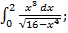 б)
б)  ;
в) ;
в)  . .
| ||
а)  б)
б)  в)
в)  . .
| а)  б)
б)  в)
в)  . .
| ||
а)  б)
б)  ;
в) ;
в)  . .
| а)  б)
б)  в)
в) 
| ||
а) 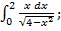 б)
б)  в)
в)  . .
| а)  б)
б)  ;
в) ;
в) 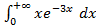 . .
| ||
а) 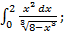 б)
б)  в)
в)  . .
| а)  б)
б)  ;
в) ;
в) 
|
ЗАДАНИЕ 5 Исследовать сходимость несобственного интеграла
| Вариант | Интеграл | Вариант | Интеграл |
а)  б)
б)  ;
в) ;
в)  . .
| а)  ;
б) ;
б) 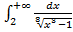 ;
в) ;
в) 
| ||
а)  б)
б) 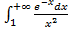 ;
в) ;
в) 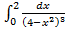 . .
| а)  б)
б)  в)
в)  . .
| ||
а)  ;
б) ;
б)  в)
в) 
| а)  ;
б) ;
б)  ;
в) ;
в) 
| ||
а)  ;
б) ;
б)  ;
в) ;
в) 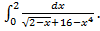
| а)  б)
б)  в)
в) 
| ||
а)  б)
б)  в)
в) 
| а) 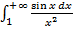 ;
б) ;
б)  ;
в) ;
в) 
|
ЗАДАНИЕ 6 Вычислить объем тела, ограниченного поверхностями
| Вариант | Уравнение поверхностей | Вариант | Уравнение поверхностей |

| 
| ||

|

| ||

| 
| ||

| 
| ||

| 
|
ВОПРОСЫ К ЭКЗАМЕНУ
1. Непосредственное интегрирование.
2. Интегрирование путем подведения под знак интеграла и методом подстановки.
3. Интегрирование по частям.
4. Интегрирование рациональных функций.
5. Интегрирование тригонометрических функций.
6. Вычисление определенного интеграла.
7. Замена переменных в определенном интеграле.
8. Интегрирование по частям в определенном интеграле.
9. Вычисление площади плоской фигуры.
10. Вычисление длины дуги плоской кривой.
11. Вычисление объема тела.
12. Двойной интеграл в прямоугольных координатах.
13. Замена переменных в двойном интеграле.
14. Вычисление площади плоской фигуры.
15. Вычисление объема тела.
16. Вычисление площади поверхности.
17. Физические приложения двойного интеграла.
18. Криволинейный интеграл по длине дуги (криволинейный интеграл 1-го рода).
19. Криволинейный интеграл по координатам (криволинейный интеграл 2-го рода).вычисление площади фигуры, ограниченной замкнутым контуром.
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ
1. Мышкис А.Д. Математика для технических вузов. Специальные курсы: учеб. пособие / А. Д. Мышкис. - 3-е изд., стер. - СПб.; М.; Краснодар: Лань, 2009. - 632 с.
2. Берман Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г. Н. Берман. - 22-е изд., перераб. - СПб.: Профессия, 2005. - 432 с.
3. Математический анализ и линейная алгебра. Учебное–методическое пособие. / Под ред. Н.Ш.Кремера - М.: ВЗФЭИ, 2002.
Дата публикования: 2015-10-09; Прочитано: 168 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
