ФАЛ двух аргументов

n=2, m=2²=4, количество функций = 2^m=2⁴=16

Функция	А= 1 0 1 0 B= 1 1 0 0	Название функции	УГО
f0 (В,А)	0 0 0 0	константа 0 f0=0
f1 (В,А)	0 0 0 1	отрицание дизъюнкции f1= , стрелка Пирса f1= или ф-ция Вебба f1=
f2 (В,А)	0 0 1 0	запрет f2=
f3 (В,А)	0 0 1 1	отрицание В f3=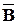
f4(В,А)	0 1 0 0	запрет f4=
f5 (В,А)	0 1 0 1	отрицание А f5=
f6 (В,А)	0 1 1 0	неравнозначность, сумма по mod2 f6=
f7 (В,А)	0 1 1 1	отрицание конъюнкции f7= 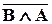, функция Шеффера f7=
f8 (В,А)	1 0 0 0	конъюнкция f8=
f9 (В,А)	1 0 0 1	равнозначность f9=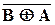
f10 (В,А)	1 0 1 0	ф-ция сохранения переменной А f10=А
f11 (В,А)	1 0 1 1	импликация f11=
f12 (В,А)	1 1 0 0	ф-ция сохранения переменной В f12=В
f13 (В,А)	1 1 0 1	импликация f13=
f14 (В,А)	1 1 1 0	дизъюнкция f14=
f15 (В,А)	1 1 1 1	константа 1 f15=1

Дадим такие определения:

ФАЛ, принимающие одинаковые значения на всех наборах аргументов, называются равными.

ФАЛ существенно зависит от аргумента Хi, если

F(X₁,X₂,...,Х_i-1, 0,X_i+1,...,X_n) и F(X₁,X₂,...,Х_i-1, 1,X_i+1,...,X_n)

В противном случае она зависит не существенно, а соответствующий аргумент называется фиктивным.

Например:

Х1 Х2 Х3 F(X1,X2,Х3)

0 0 0 0

0 0 1 0

0 1 0 1

0 1 1 1

1 0 0 0

1 0 1 0

1 1 0 1

1 1 1 1

Видно, что Х3 – фиктивный аргумент. Это показывает, что в функцию можно ввести любое число фиктивных аргументов, от которых она существенно не зависит. Этот прием в дальнейшем потребуется для выполнения ряда преобразований.

Рассмотренные логические функции введены формально. Однако им можно придавать определенный "логический" смысл. Алгебра логики часто называется исчислением высказываний.

Рассмотрим, какое смысловое содержание можно вложить в некоторые сложные высказывания на примере ФАЛ одного и двух аргументов.

1. Отрицание. НЕ (NOT)

Унарная, т. е. одноместная операция. Записывается в виде А.

Отрицанием некоторого высказывания А является такое высказывание, которое истинно, когда А ложно, и ложно, когда А истинно.

Например, отрицанием высказывания "Точка М лежит на прямой a" будет высказывание "Точка М не лежит на прямой а".

Определение отрицания может быть записано в виде следующей истинностной таблицы:

А	А
и	л
л	и

2. Конъюнкция. И (AND)

Conjunctio (лат.) – соединяю. В математической логике обозначают Ù или &. Это бинарная, т.е. двухместная операция.

Конъюнкцией двух высказываний A и B называют такое высказывание, которое истинно тогда и только тогда, когда истинны оба высказывания A и B.

Записывается как A Ù B.

Например, высказывание "Число 2 – простое и число 2 – четное".

Неравенство | x-1| < 2, которое своим решением имеет конъюнкцию (-1< x) и (х < 3).

Решим:

,объединив эти решения, получим ответ

Решением уравнения | x-1| + | y-2| = 0 будет конъюнкция x=1 Ù y=2.

Всякая система уравнений, например: представляет собой по существу конъюнкцию f (x,y)=0 Ù g (x,y)=0.

Определение конъюнкции может быть записано в виде следующей истинностной таблицы:

A	B	A ÙB
и	и	и
и	л	л
л	и	л
л	л	л

3. Дизъюнкция. ИЛИ (OR)

Disjunctio (лат.) – разбиение, различие. В математической логике обозначают Ú. Это бинарная, т.е. двухместная операция.

Дизъюнкцией двух высказываний A и B называют такое высказывание, которое истинно тогда и только тогда, когда истинно хотя бы одно из этих высказываний.

Записывается как A Ú B.

Например, высказывание "2 < 3 или 2 = 3" является истинным, высказывание "2 > 3 или 2 = 3" всегда ложно.

Неравенство | x-1| > 2 в качестве своего решения дает нам совокупность неравенств:

ответ:

Решая неравенство , используем конъюнкцию совместно с дизъюнкцией:

.

Определение дизъюнкции может быть записано в виде следующей истинностной таблицы:

A	B	A ÚB
и	и	и
и	л	и
л	и	и
л	л	л

Дизъюнкции ставится в соответствие схема, состоящая из параллельного соединения контактов, а конъюнкции – из последовательного. Нетрудно убедиться в выполнимости аксиом 1-8.

4. Импликация (условное высказывание).

В русском языке выражается с помощью высказывательных форм " если А, то В ", " когда А, тогда В ", " из А следует В ", " В при условии, что А " и т.п.

Выражение А называется посылкой или основанием, выражение В называется следствием или заключением.

Это бинарная операция. Обозначается А Þ В (А ® В).

Если импликация А Þ В истинна, то говорят, что

а) В – следствие из А, или

б) В следует из А, или

в) А достаточное условие для В, или

г) В необходимое условие для А.

Импликацией "если А, то В" называется такое высказывание, которое ложно тогда и только тогда, когда А истинно, а В ложно.

Например, высказывание "Если x делится на 3, то х+9 делится на 3" является истинным при любом целом значении переменной х (по теореме: если слагаемые делятся на некоторое число, то и их сумма делится на это число).

Высказывание: "Если многоугольник правильный, то возле него можно описать окружность". Это теорема, доказываемая в школьном курсе математики. Истинность этого высказывания обозначает, что мы не можем найти такой правильный многоугольник, около которого нельзя описать окружность.

Определение импликации может быть записано в виде следующей истинностной таблицы:

A	B	А Þ В
и	и	и
и	л	л
л	и	и
л	л	и