 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Основные теоретические сведения. Наряду с вопросами движения жидкостей по трубам и каналам, на практике приходится решать задачи, связанные с истечением жидкости из отверстий и насадков
|
|
Наряду с вопросами движения жидкостей по трубам и каналам, на практике приходится решать задачи, связанные с истечением жидкости из отверстий и насадков.
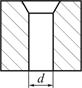
Насадком называют короткий патрубок, присоединенный к отверстию. Различают следующие основные типы насадков (рис. 1.10).

| 
| 
|
| а | б | в |
| Рисунок Рисунок 1.10 – Типы насадков: Рисунок а – внешний цилиндрический насадок (насадок Вентури); б – внутренний цилиндрический насадок (Насадок Борда); в – конический сходящийся насадок |
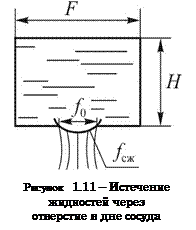
При истечении жидкости через отверстие в дне сосуда (рис. 1.11) сила напора  затрачивается на создание скорости истечения жидкости w и преодоления сопротивления в отверстии. Если это сопротивление отсутствует, т.е. происходит истечение идеальной жидкости, то согласно уравнению Бернулли весь статический напор в отверстии переходит в скоростной, м3/с:
затрачивается на создание скорости истечения жидкости w и преодоления сопротивления в отверстии. Если это сопротивление отсутствует, т.е. происходит истечение идеальной жидкости, то согласно уравнению Бернулли весь статический напор в отверстии переходит в скоростной, м3/с:
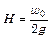 , м или
, м или  . (1.37)
. (1.37)
 При этом объем идеальной жидкости, вытекающей из сосуда за одну секунду,
При этом объем идеальной жидкости, вытекающей из сосуда за одну секунду,
 (1.38)
(1.38)
где 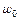 – скорость движения жидкости в отверстии, м/с;
– скорость движения жидкости в отверстии, м/с; 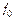 – площадь отверстия, м2.
– площадь отверстия, м2.
Однако в действительности количество вытекающей жидкости меньше вычисленного по уравнению (1.38) вследствие двух причин:
Во-первых, фактическая скорость истечения жидкости из отверстия вследствие потери напора на преодоление трения в отверстии меньше теоретической  :
:
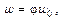
где j – коэффициент скорости, представляющей собой отношение действительной скорости истечения к теоретической: значение его определяется по опытным данным и находится в пределах 0,99—0,96.
Во-вторых, площадь сечения струи f меньше площади отверстия 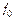 вследствие сжатия струи на выходе из отверстия:
вследствие сжатия струи на выходе из отверстия:
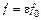 ,
,
где e – коэффициент сжатия струи: отношение площади сечения струи в месте ее наибольшего сжатия 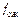 к сечению отверстия
к сечению отверстия 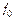 .
.
Таким образом, расход реальной жидкости при истечении из отверстия при постоянном уровне жидкости в сосуде определяется уравнением
 . (1.39)
. (1.39)
Произведение коэффициента сжатия струи  на коэффициент скорости j называется коэффициентом расхода и обозначается a . Следовательно,
на коэффициент скорости j называется коэффициентом расхода и обозначается a . Следовательно, 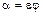 и уравнение расхода через отверстие принимает следующий вид:
и уравнение расхода через отверстие принимает следующий вид:
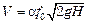 . (1.40)
. (1.40)
Коэффициент расхода a показывает, во сколько раз расход реальной жидкости через отверстие меньше теоретического расхода идеальной жидкости, и его величина всегда меньше единицы.
 При истечении жидкости через отверстие в боковой стенке (рис. 1.12) напор не будет одинаковым для всех точек по сечению отверстия и уравнение расхода, строго говоря, будет применимо только для элемента сечения высотой
При истечении жидкости через отверстие в боковой стенке (рис. 1.12) напор не будет одинаковым для всех точек по сечению отверстия и уравнение расхода, строго говоря, будет применимо только для элемента сечения высотой 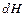 . В этом случае расход жидкости может быть точно определен только путем суммирования, т.е. интегрирования элементарных расходов по всему сечению отверстия. Однако в технических расчетах для отверстия в тонкой боковой стенке можно с достаточной точностью пользоваться теми же расчетными уравнениями, что и для отверстия в дне сосуда. Лишь для отверстий больших размеров следует учитывать изменения коэффициента расхода, значения которых приводятся в справочниках.
. В этом случае расход жидкости может быть точно определен только путем суммирования, т.е. интегрирования элементарных расходов по всему сечению отверстия. Однако в технических расчетах для отверстия в тонкой боковой стенке можно с достаточной точностью пользоваться теми же расчетными уравнениями, что и для отверстия в дне сосуда. Лишь для отверстий больших размеров следует учитывать изменения коэффициента расхода, значения которых приводятся в справочниках.
При истечении жидкости через короткий цилиндрический патрубок (насадок) происходит дополнительная потеря энергии, главным образом вследствие внезапного расширения струи в патрубке. Поэтому скорость истечения жидкости через патрубок меньше скорости ее истечения через отверстие в тонкой стенке. Вместе с тем, расход жидкости, вытекающей через патрубок, больше, чем при истечении через отверстие, так как струя в патрубке сначала сжимается, а затем расширяется и вытекает, заполняя все его сечение. Поэтому коэффициент сжатия струи на выходе из патрубка e = 1, что приводит к значительному возрастанию коэффициента расхода и, соответственно, к увеличению расхода жидкости.
Насадки различной геометрической формы при одной и той же площади отверстий имеют разные численные значения коэффициентов скорости и коэффициентов расхода. При этом коэффициент расхода a в случае достаточно больших значений критерия Рейнольдса не зависит от режима движения жидкости. При малых же числах Re (Re < 50) коэффициент расхода a существенно зависит от Re: с уменьшением критерия Рейнольдса величина a также уменьшается. Для круглых отверстий эта зависимость может быть представлена в виде следующих уравнений:
при Re < 25 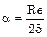 ;
при 25 < Re < 300 ;
при 25 < Re < 300 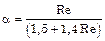 ;
при 300 < Re < 10000 ;
при 300 < Re < 10000 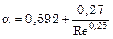 ;
при Re > 10000 ;
при Re > 10000 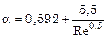 . .
| (1.41) |
В том случае, когда уровень жидкости в сосуде переменный, справедливо балансовое равенство
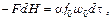
где 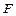 – площадь поперечного сечения сосуда, м2; t – время истечения жидкости из сосуда, с.
– площадь поперечного сечения сосуда, м2; t – время истечения жидкости из сосуда, с.
Если в это равенство подставить значение скорости из уравнения (1.37) и решить его относительно t, то получим выражение для определения времени истечения жидкости из сосуда с переменным уровнем ее в нем:
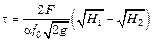 . (1.42)
. (1.42)
Пользуясь выражением (1.42), можно определить коэффициент расхода, если известно время, за которое понизился уровень жидкости в сосуде от 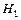 до
до  :
:
 . (1.43)
. (1.43)
При этом время полного опорожнения сосуда
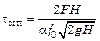 , (1.44)
, (1.44)
где  – первоначальный уровень жидкости в сосуде.
– первоначальный уровень жидкости в сосуде.
Дата публикования: 2015-10-09; Прочитано: 319 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
