П.2 Предел функции

Часть I. Последовательности, пределы, производная.

П.1. Числовые последовательности и пределы.

Пусть задано такое множество {c1,c2,¼,c4,¼} пронумерованных действительных чисел, что по номеру элемента мы можем назвать числовое значение данного элемента, а по числовому значению элемента его номер в данном множестве. Тогда говорят, что задана числовая последовательность.

Числовая последовательность обозначается {c_n} или просто c_n.

Существуют различные способы задания числовых последовательностей.

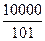1) Формулой общего члена c_n=(-1)ⁿ Откуда c₁= , c₂= , c₃= , c₄= , ¼c₁₀₀= ,¼

2) перечислением элементов последовательности 1, , , ¼ Откуда c_n=

Определение1. Число а называется пределом последовательности {c_n}, если
"e>0 $ n₀ "n>n₀ ½c_n-а½<e (Для любого положительного числа e, существует такой номер n₀, что для всех номеров n>n₀ модуль ½c_n-а½<e). Обозначается

Пример1. c_n= . Покажем, что данная последовательность имеет своим пределом число 0. Пусть e- произвольное число большее 0 (на самом деле очень малое). Надо найти такой номер n₀, что все элементы c_n0+1, c_n0+2, ¼, c_n0+k,¼(т.е. n>n₀) удовлетворяют условию ½c_n-а ½< e (c_n= , а=0). Решим это неравенство: ½ -0 ½<e, <e, n> , достаточно взять n₀= [1/e]- целая часть числа 1/e. Тогда для всех n 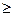[1/e]+1 неравенство выполняется. Следовательно

Определение2. Последовательность {c_n} называется бесконечно малой, если

, т.е. "e>0 $ n₀ "n>n₀ êc_n½< e.

Определение3. Последовательность {c_n} называется бесконечно большой, если

т.е."E>0 $ n₀ "_n>n₀ ½c_n½>E

Пример 2. Последовательности {a_n}= 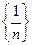, { b_n}= , {g_n}= , {d_n}= - бесконечно малые. Здесь n!=1,2,3¼n. 0!=1, 1!=1, 2!=1×2=2, 3!=1×2×3=6, 4!=1×2×3×4=24 и т.д.

Последовательности {c_n}={n}, {y_n}={n²},{z_n}={2ⁿ}- бесконечно большие.

Свойства предела последовательности.

1°. Если и а > r (а < r), то начиная с некоторого номера х_n> r (x_n< r).

Доказательство. Т.к. , то "e>0 $ n₀ "n>n₀ ½x_n-a ½<e или -e< x_n-a <e или а-e< х_n<a+e.

Т.е. в e- окрестности точки а (в интервале (а-e, а+e)) cодержатся все элементы последовательности , начиная с номера n₀+1.

Пусть а>r. Т.к. e- любое число, положительное, выберем его так, чтобы а-Е было больше r

а-e

r а х (Можно взять e= )

Тогда " n>n₀ r< а-e < х_n< a+e, т.е. х_n>r. Аналогично для случая а< r.

2°. Если последовательность имеет предел, то он единственный.

3°. Если {х_n}={у_n}, то

4°. Если х_n< у_n, то

5°. Если х_n у_n, то

6°. (Лемма о двух милиционерах) Пусть х_n у_n z_n (или х_n< у_n< z_n), ,

Тогда последовательность у_n имеет предел

Доказательство. Т.к. , то "e< 0 $ n₁ "n>n₁ a-e< x_n< a+e (1)

Т.к. , то "e>0 $ n₂ "n>n₂ a-e< z_n < a+e (2).

Пусть n₀=max {n_1, n₂ }, тогда " n>n₀ выполнено и неравенство (1) и неравенство (2), т.е." n>n₀ a-e<x_n£ у_n£ z_n< a+e, т.е. a-e< у_n<a+e, т.е.

Теорема 1. 1. (Связь между сходящимисяи бесконечно малыми)Последовательность {a_n}- бесконечно малая тогда и только тогда, когда последовательность - бесконечно большая (схематически это будет означать =¥).

2. Последовательность {x_n}- бесконечно большая тогда и только тогда, когда последовательность -бесконечно малая (схематически =0).

Определение4. Последовательность{x_n} называется сходящейся, если она имеет конечный предел, последовательность{x_n} называется расходящейся если она не имеет предела или её предел равен ¥. Говорят, что сходящаяся последовательность сходится к числу

Теорема2. Последовательность{x_n} является сходящейся (сходится к числу а) тогда и только тогда, когда последовательность {х_n-a}-бесконечно малая.

Из этой теоремы получаем, если , то a-x_n=a_n, где a_n- бесконечно малая, тогда а=х_n+a_n. Т.е. Û a=x_n+a,где a_n-бесконечно малая.

Теорема3. (арифметические операции над сходящимися последовательностями)

Пусть , , тогда

1. =a±b

2. =a×b

3. при b¹0 =

П.2 Предел функции.

Определение1. Число а называется пределом функции у=f(х), при х стремящемся к х₀ (), если для любой последовательности{x_n} сходящейся к x₀ последовательность{f(x_n)=y_n} сходится к а.

Из определения 1 следует, что для предела функции справедливы все теоремы, справедливые для предела последовательности.

Определение2. Число а называется пределом функции у=f(x) при х стремящимся к х₀ (),если "e>0 $ d>0 "х ½х-х₀½<dÞ½f(x)-a½<e. Легко показать, что определение1 равносильно определению2. Мы будем пользоваться обоими этими определениями.

Теорема1. (1-ый замечательный предел)

Доказательство.1)Пусть х>0, т.е. х-угол, измеренный в радианах, лежащий в 1-ой четверти. Дан тригонометрический круг (окружность радиуса R=1). Рассмотрим треугольник ОАВ, сектор ОАВ и треугольник ОСВ.

S_OAB< S_{сектора}< S_OCB

ОВ ·АН< хR< ОВ·СВ

OB·AH<xR<OB·CB

OB=R=1, AH=sinx, CB=tgx.

Таким образом 0<sinx<x<tgx. Поделим все части этого неравенства на sinx>0.

0<1< < . Перевернём все дроби

0<cosx< 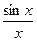<1. (1)

При х®0, cosx®1, 1®1.

По лемме о 2-х милиционерах 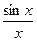®1при х®0.

2) Пусть -х<0, т.е. –х-угол в IV четверти. В неравенстве (1) везде вместо х подставим -х

cos(-x)=cosx, = =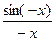

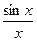
Ни одна величина в (1) не изменилась, значит неравенство справедливо при -хÎIV четверти. Теорема1 доказана.

Теорема2. (2-ой замечательный предел)

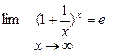(или в равносильной формулировке ).

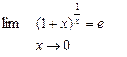Теорема3. (Бином Ньютона)

, где

или в более подробной записи

(а+b)ⁿ=aⁿ+na^n-1b+C_n²a^n-2b²+C_n³a^n-3b³+¼+C_n^n-2a²b^n-2+na^n-1b+bⁿ.

П.3 Определение производной. Таблица производных.

Определение1. Пусть у=f(x)-произвольная функция, х₀-значение аргумента получило приращение х и стало равным х. х=х-х₀ (приращение может быть отрицательным), тогда функция изменила своё значение с у₀=f(x₀) до y₁=f(x₁),т.е. функцияy=f(x) получила приращение у= f(x)=f(x)-f(x₀). Если существует конечный предел , то он называется производной функции в точке х₀.

Из определения производной и теоремы о связи между сходящейся и бесконечно малой следует

=f¢(x₀)+a(x), где a(x)®0 при x®0 или f(x)=f¢(x₀) x+a(x) x (1)

Определение2. Функция f(x) непрерывна в точке х₀, если =f(x₀) (2)

Из (1) следует что если функция имеет производную в точке х₀, то она в этой точке непрерывна.

Теорема 1. Сумма, разность, произведение 2-х функций, непрерывных в точке х₀, непрерывно в точке х=х₀. Частное 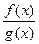двух непрерывных в точке х₀ функций непрерывно в точке х₀, если g(x₀)¹0.

Доказательство этой теоремы следует из теоремы об арифметических операциях над сходящимися последовательностями (функциями) и определения непрерывной функции (формула(2)).

Определение3. Пусть даны две функции у=f(u) и U=Y(x), y=F(x)=f(Y(x)) называется их суперпозицией (у=F(x) называется сложной функцией).

Пример1. y=cosx², y=cosu, u=x²,

y=e^tgx y=e^u u=tgx

Теорема2.(о производной сложной функции)

Пусть у=f(u) и u=Y(x) имеют производные в точках u₀ и х₀ соответственно, причём u₀=Y(x₀), то y=F(x)=f(Y(x)) имеет производную в точке х₀ и

F¢(x₀)=f(Y(x₀))¢=f¢(u₀)Y¢(x₀).

Доказательство. Из(1) Df=f¢(u₀)Du+a₁(u)Du, (4)

DY=Y¢(x₀)Dx+a₂(x)Dx, (5)

a₁(u)-бесконечно малая при Du®0, a₂(х)-бесконечно малая при Dх®0

Т.к. функция u=Y(x) имеет производную в точке х₀, то Y(x) непрерывна в точке х₀, следовательно при Dх®0 Du=DY(x)®0,т.е.a₁(u) будет бесконечно малой при Dх®0.

Разделим (4) на Dх, получим =f¢(x₀) +a₁(u) , u=Y(x), значит

=f¢(x₀) +a₁(Y) .

Перейдём к пределу при Dх®0

lim =F¢(x)=f¢(u₀)lim +lima₁(Y) =f¢(x₀)Y¢(x₀)+0=f¢(x₀)Y¢(x₀).

Определение4. Пусть у=f(x) определена, непрерывна и строго убывает (возрастает) в некоторой окрестности точки х₀, тогда существует функция х=f ^-1(y)- которая называется обратной к у=f(x) в некоторой окрестности точки у₀₌f(x₀), при этом f(f^-1(y))=y, f^-1(f(x))=x.