Тема 2.4.2. Логические элементы, цифровые устройства

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным вам правилам.

Сложение. Рассмотрим сложение чисел в двоичной системе счисления. В его основе лежит таблица сложения одноразрядных двоичных чисел:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10

Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания.

Сложение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов в старшие. В качестве примера сложим в столбик двоичные числа 110₂ и 11₂:

Проверим правильность вычислений сложением в десятичной системе счисления. Переведем двоичные числа в десятичную систему счисления и затем их сложим:

110₂ = 1 × 2² + 1 × 2¹ + 0 × 2⁰ = 6₁₀;

11₂ = 1 × 2¹ + 1 × 2⁰ = 3₁₀;

6₁₀ + 3₁₀ = 9₁₀.

Теперь переведем результат двоичного сложения в десятичное число:

1001₂ = 1 × 2³ + 0 × 2² + 0 × 2¹ + 1 × 2⁰ = 9₁₀.

Сравним результаты - сложение выполнено правильно.

Вычитание. Рассмотрим вычитание двоичных чисел. В его основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой:

Вычитание многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей вычитания с учетом возможных займов из старших разрядов. В качестве примера произведем вычитание двоичных чисел 110₂ и 11₂:

Умножение. В основе умножения лежит таблица умножения одноразрядных двоичных чисел:

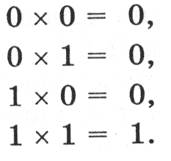
Умножение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на цифры множителя. В качестве примера произведем умножение двоичных чисел 110₂ и 11₂:

Деление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. В качестве примера произведем деление двоичного числа 110₂ на 11₂:

Арифметические операции в восьмеричной и шестнадцатеричной системах счисления. Аналогично можно выполнять арифметические действия в восьмеричной и шестнадцатеричной системах счисления. Необходимо только помнить, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления:

Для проведения арифметических операций над числами, выраженными в различных системах счисления, необходимо предварительно перевести их в одну и ту же систему.

Задания

1. Провести сложение, вычитание, умножение и деление двоичных чисел 10102 и 102 и проверить правильность выполнения арифметических действий с помощью электронного калькулятора.

1. Сложить восьмеричные числа: 5₈ и 4₈, 17₈ и 41₈.

1. Провести вычитание шестнадцатеричных чисел: F16 и А16, 4116 и 1716.

1. Сложить числа: 17₈ и 17₁₆, 41₈ и 41₁₆

Лабораторная работа № 3. Системы счисления: перевод чисел

Лабораторная работа № 4. Арифметические операции над двоичными числами

Лабораторная работа № 5. Логические основы работы ПК