 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Энтропия, среднее количество информации в принятом сообщении
|
|
При передаче дискретных сообщений по ДКС различают следующие энтропии:
ü 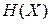 - безусловная энтропия источника, или среднее количество информации на символ, выдаваемое источником.
- безусловная энтропия источника, или среднее количество информации на символ, выдаваемое источником.
ü  – безусловная энтропия приемника или среднее количество информации на символ, получаемое приемником.
– безусловная энтропия приемника или среднее количество информации на символ, получаемое приемником.
ü  – условная энтропия Y относительно Х, или мера количества информации в приемнике, когда известно, что передается Х. Эта энтропия характеризует количество ложной информации, создаваемой помехами:
– условная энтропия Y относительно Х, или мера количества информации в приемнике, когда известно, что передается Х. Эта энтропия характеризует количество ложной информации, создаваемой помехами:
 (7.21)
(7.21)
ü 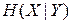 – условная энтропия X относительно Y, или мера количества информации об источнике, когда известно, что принимается Y. Характеризует количество информации, потерянной за счет помех:
– условная энтропия X относительно Y, или мера количества информации об источнике, когда известно, что принимается Y. Характеризует количество информации, потерянной за счет помех:
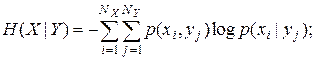 (7.22)
(7.22)
Условную энтропию можно так же представить в виде
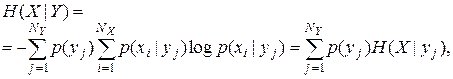
где величина
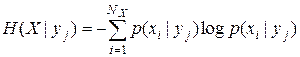 (7.23)
(7.23)
называется частной условной энтропией. Она характеризует неопределенность состояния системы А (передатчика) в случае, когда известно состояние  у наблюдаемой системы В (приемника). Зафиксировав состояние
у наблюдаемой системы В (приемника). Зафиксировав состояние  системы В, мы тем самым изменяем комплекс условий, при которых может реализоваться событие
системы В, мы тем самым изменяем комплекс условий, при которых может реализоваться событие 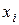 . Это обнаруживается как изменение вероятности реализации события
. Это обнаруживается как изменение вероятности реализации события 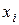
 (имеет место статистическая зависимость). Если до изменения условий указанная вероятность была равна безусловной (полной) вероятности
(имеет место статистическая зависимость). Если до изменения условий указанная вероятность была равна безусловной (полной) вероятности  , то после изменения условий она стала равной условной вероятности
, то после изменения условий она стала равной условной вероятности 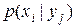 . При отсутствии статистической зависимости
. При отсутствии статистической зависимости
 , поскольку
, поскольку

При наличии статистической зависимости энтропия 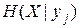 может оказаться как меньше, так и больше
может оказаться как меньше, так и больше  . Напомним, что для энтропии
. Напомним, что для энтропии 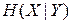 всегда справедливо неравенство
всегда справедливо неравенство
.
ü  – совместная энтропия системы передачи (энтропия объединения) – средняя информация на пару (переданного и принятого) символов:
– совместная энтропия системы передачи (энтропия объединения) – средняя информация на пару (переданного и принятого) символов:
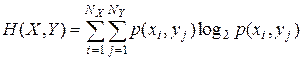 . (7.24)
. (7.24)
Для независимых систем


Для зависимых систем
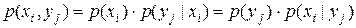
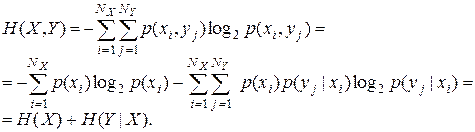
В качестве примера вычислим энтропии  ,
, 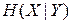 ,
, 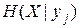 и взаимную информацию
и взаимную информацию 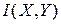 , когда системы А и В описываются двумерным распределением
, когда системы А и В описываются двумерным распределением 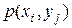 , заданным в виде табл. 7.1. Вычисленные значения условной вероятности
, заданным в виде табл. 7.1. Вычисленные значения условной вероятности 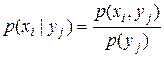 записаны в табл. 7.2
записаны в табл. 7.2
Таблица 7.1. Двумерное распределение 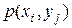
 X
y X
y
| x1 | x2 | p (yj) |
| y1 y2 |  =0,5 =0,5
 =0,25 =0,25
| 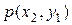 =0 =0
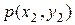 =0,25 =0,25
| 0,5 0,5 |
| p (xi) | 0,75 | 0,25 |
Таблица 7.2. Условные вероятности
 X
y X
y
| x1 | x2 |
| y1 y2 | 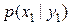 =1 =1
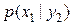 =0,5 =0,5
|  =0 =0
 =0,5 =0,5
|
Используя записанные в таблицах значения вероятностей, получим
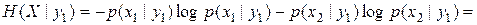



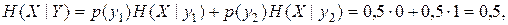

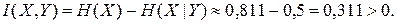
Отсюда
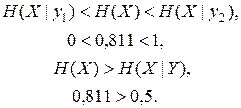
Дата публикования: 2015-09-17; Прочитано: 880 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
