Нахождение корней алгебраических уравнений

1. Алгебраическое уравнение нулевой степени 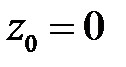корней не имеет.

2. Алгебраическое уравнение первой степени 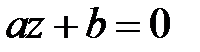имеет один корень , .

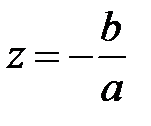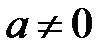3. Корни алгебраического уравнения второй степени 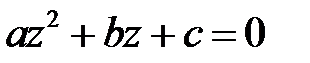находятся по формулам:

а) ,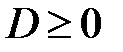

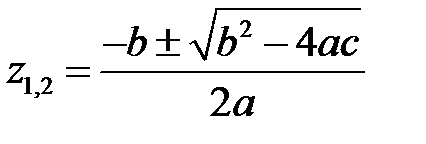
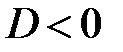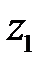б) , , причём и 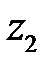взаимно сопряженные числа.

4. Корни двучленного алгебраического уравнения 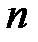-го порядка 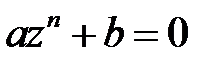находят по формуле .

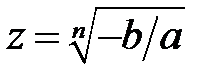Определение 2.3. Корень 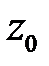многочлена 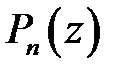называется корнем кратности 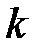, если 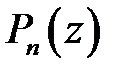делится (без остатка) на 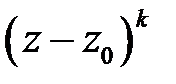, но не делится на .

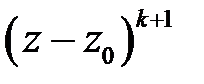Если 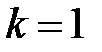, то корень называется простым.

Теорема 2.2. (теорема Гаусса, основная теорема алгебры). Уравнени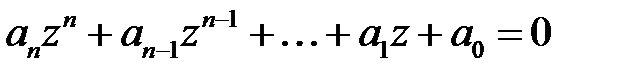е , где 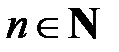, 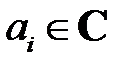имеет хотя бы один корень (в общем случае комплексный).

Следствие 2.1. Многочлен степени 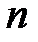с комплексными коэффициентами и со старшим коэффициентом 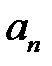имеет ровно 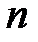корней и разлагается в произведение 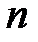сомножителей вида 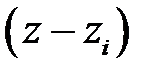, т. е. 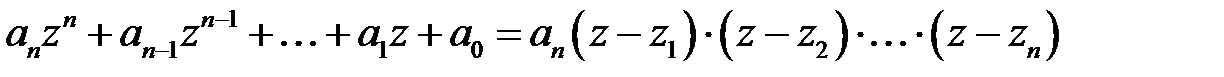, и это представление единственно с точностью до перестановки сомножителей.