Пример решения задания

Дан ПИ-регулятор с ПФ вида W_p = 2 + и объект управления, описываемый дифференциальным уравнением

.

Определяется передаточная функция объекта:

.

Тогда передаточная функция разомкнутой системы имеет вид

.

ХВЗС:

D(s) = A(s) + B(s) = 2s⁴ + 3s³ + s² + 2s³ + 9s² + 6s + 1 = 2s⁴ + 5s³ + 10s² + 6s + 1.

Передаточные функции замкнутой системы:

- по заданию,

- по ошибке,

- по возмущению.

По передаточным функциям определяются коэффициенты усиления путем подстановки в них s = 0:

К_з = Ф_з(0) = 1 – по заданию;

К_Е = Ф_Е(0) = 0 – по ошибке;

К_в = Ф_в(0) = 0 – по возмущению.

Устойчивость АСР определяется по критерию Гурвица.

Поскольку коэффициенты ХВЗС а₄ = 2, а₃ = 5, а₂ = 10, а₁ = 6, а₀ = 1 (степень полинома n = 4), то матрица Гурвица имеет вид

(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители:

Δ₁ = 5 > 0,

,

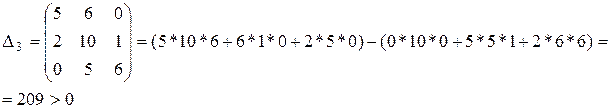
Δ₄ = 1* Δ₃ = 1*209 > 0.

Поскольку все определители положительны, то АСР устойчива. ♦

Варианты заданий

Вариант	ПФ регулятора	Дифференциальное уравнение ОУ
	Wp = 4 + ;
	Wp = 5 + ;
	Wp = 0,5
	Wp = 2 + ;
	Wp = 1 + ;
	Wp = 4
	Wp = 5 + ;
	Wp = 8
	Wp = 4 + ;
	Wp =
	Wp = 1 + ;
	Wp = 1 +
	Wp = 5 + ;
	Wp = 1 + ;
	Wp = ;
	Wp = 1 + ;
	Wp = 1 + ;
	Wp = 2
	Wp = 4
	Wp = ;
	Wp = 2 + ;
	Wp = 1 + ;
	Wp = 0,5 + ;
	Wp = 0,1
	Wp = 0,2 + ;
	Wp = 2 + ;