Примеры решения задач Коши

Таблица 1

x	x 0	x 1	…	xn = b
y	y 0	y 1	…	yn» y (b)

при этом расчётными точками метода служат узлы сетки: x _i = x ₀ + ih (i = 1, …, n).

Геометрический способ – метод ломаных Эйлера.

Пользуясь тем, что для задачи Коши:

y ¢(x) = f (x, y), x Î(r 1, r 2) = [ x 0, b ] y (x 0) = y 0

(3) (4)

в точке x ₀ известно и значение решения y (x ₀) = y ₀ и значение его производной
y ¢(x ₀) = f (x ₀, y ₀), можно записать уравнение касательной к графику искомой функции y = y (x) в точке (x ₀, y ₀).

Напомним, что уравнение касательной к кривой y = f (x) в точке (x ₀, y ₀) имеет вид:

y - y ₀ = y ¢₀(x - x ₀), где y ¢₀ = y ¢(x ₀). (14)

В данном случае в соответствие с (3) y ¢(x ₀) = f (x ₀, y ₀), поэтому уравнение касательной к графику искомой функции y = y (x) в точке (x ₀, y ₀) имеет вид:

y - y ₀ = f (x ₀, y ₀)×(x - x ₀) или

y = y ₀ + f (x ₀, y ₀)×(x - x ₀) (15)

В соответствии с уравнением (15) ордината рассматриваемой касательной в ближайшем к x ₀ узле x ₁ = x ₀ + ih будет равна:

y ₁ = y ₀ + f (x ₀, y ₀)×(x ₁ - x ₀) или

y ₁ = y ₀ + h f (x ₀, y ₀) (16)

Поскольку мы считаем функцию y (x) непрерывной по условию, то при достаточно малом шаге h ордината y ₁ рассматриваемой касательной в ближайшем к x ₀ узле x ₁ должна мало отличаться от значения ординаты y (x ₁) решения y (x) задачи (3), (4) в точке x ₁. Следовательно, точка (x ₁, y ₁), лежащая на касательной y = y ₀ + y ¢₀(x - x ₀) и являющаяся её точкой пересечения с линией x = x ₁, может быть приближенно принята за приближённое значение решения y = y (x) в узле x ₁ (рис. 3) или может быть приближённо принята за новую начальную точку.

Далее через точку (x ₁, y ₁) снова проведём прямую:

y = y ₁ + f (x ₁, y ₁)×(x - x ₁) (17)

которая уже приближённо отражает поведение касательной к решению y = y (x) в точке (x ₁, y (x ₁)).

Рисунок - 3 Метод ломаных Эйлера

Далее, как и на предыдущем шаге, ищем точку пересечения (y ₂) прямой (17) и линии x = x ₂. Для этого в уравнение прямой (17) вместо x подставляем значение
x ₂ = x ₁ + h.

y ₂ = y ₁ + f (x ₁, y ₁)×(x ₂ - x ₁) или

y ₂ = y ₁ + hf (x ₁, y ₁) (18)

Точка y ₂ принимается за приближённое значение решения y = y (x) в узле x ₂.

Продолжая этот процесс далее по схеме (15) - (18) вплоть до точки x_n = b мы сможем сформировать искомую таблицу 1 приближённых значений решения y = y (x) в узлах x_i = x ₀ + ih (i = 1, …, n).

y_{i +1} = y_i + h f (x_i, y_i) (19)

В итоге, при реализации схемы (19), называемой методом Эйлера, график решения y = y (x) данной задачи коши (3), (4) приближённо представляется ломаной, составленной из отрезков «приближённых касательных» (рис. 3), что оправдывает другое название метода Эйлера, как метода ломаных.

Квадратурный способ вывода метода Эйлера.

Как было показано ранее, начальную задачу для ОДУ:

y ¢(x) = f (x, y), x Î(r 1, r 2) = [ x 0, b ] y (x 0) = y 0

(3) (4)

можно заменить эквивалентным интегральным уравнением:

(5)

Подставим в формулу (5) вместо x значение x ₁ первого узла сетки, в результате получим равенство:

(20)

Применяя к интегралу на интервале [ x ₀, x ₁] простейшую (одношаговую) формулу левых прямоугольников:

,

получим следующую приближённую формулу:

или

(21)

которая совпадает с формулой (16), описывающей первую итерацию метода ломаных Эйлера.

Далее приближённо сформулируем начальную задачу (т.е. задачу Коши) уже для узла x ₁:

y ¢(x) = f (x, y), x Î [ x 1, b ] y (x 1)» y 1 = y 0 + h f (x 0, y 0)

(22)

которая (вследствие приближённого характера начального условия y (x ₁)» y ₁ приближённо эквивалентна следующему интегральному уравнению:

(23)

Подставляя в формулу (23) вместо x значение x ₂ второго узла сетки получаем:

(23)

Вычисляя интеграл в выражении (23) по формуле левых прямоугольников на интервале [ x ₁, x ₂], получим:

.

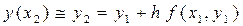Продолжая этот процесс далее, и предполагая, что на каждом i -м шаге в роли начальной точки (x ₀, y ₀) выступает точка (x_i, y_i), для приближённого значения решения y (x) на (i + 1) -м шаге сетки, получим:

(24)

И вычисляя интеграл в выражении (24) по формуле левых прямоугольников на интервале [ x_{i+ 1}, x_i ], получим формулу метода Эйлера:

(25)

Зная ошибку квадратурной формулы прямоугольников, можно оценить ошибку, получаемую на каждом шаге данной процедуры вычисления таблицы решений ОДУ.

Замечание.

В отличие от метода последовательных приближений, являющегося итерационным по сути, все рассматриваемые численные схемы решения задачи Коши для ОДУ, и в частности, метод Эйлера, являются итерационным лишь по форме. В действительности, это шаговые методы, в которых на каждом шаге выполняются однотипные действия; а характерного для сути итерационных методов уточнения решения здесь не происходит (т.е. на каждом очередном шаге метода Эйлера мы не уточняем решение, а находим его приближённое значение в другой точке сетки).

§5. Модификации метода Эйлера.

Рассмотрим квадратурную реализацию метода Эйлера, которая выражается формулами (21) - (25). Очевидно, что при применении к интегральному равенству (24) других простейших квадратурных формул (кроме уже рассмотренной квадратурной формулы левых прямоугольников), будут получаться новые численные методы решения задачи Коши (3), (4).

Модификация по формуле правых прямоугольников.

Если в равенстве (24) использовать простейшую квадратурную формулу правых прямоугольников, то получаем следующую схему решения задачи Коши:

, (i = 0,1, …, n) (26)

Метод (26) называют неявным или обратным методом Эйлера, поскольку для вычисления неизвестного значения по известному (приближённому!) значению требуется решать, в общем случае, не линейное относительно уравнение (26).

Модификация по формуле трапеций. Если в формуле

(24)

на каждом шаге использовать простейшую квадратурную формулу трапеций:

,

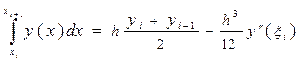где x _i – некоторая, вообще говоря, неизвестная точка интервала (x_i, x_{i+ 1}), то, отбросив слагаемое 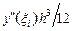приходим к следующему приближённому и также неявному методу решения задачи Коши, который называется неявным методом трапеций.

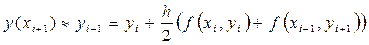, (i = 0,1, …, n) (27)

При построении квадратурных формул отмечалось, что погрешность численного интегрирования функции по формулам левых и правых прямоугольников убывает по линейному закону, т.е. пропорционально шагу h, а ошибка квадратурной формулы трапеций убывает пропорционально h ². Отсюда следует, что порядок точности неявного метода трапеций выше на единицу, чем порядка точности явного и неявного метода Эйлера (т.е. метода левых и правых прямоугольников).

Метод Хьюна - комбинация метода Эйлера и неявного метода трапеций.

Рассмотрим выражение (27) определяющее неявный метод трапеций. Если в правую часть формулы (27) вместо неизвестного значения y_{i +1} подставить значение найденного для него хорошего приближения, например, по формуле Эйлера:

, (25)

то получаем гибридный метод решения задачи Коши:

, (i = 0,1, …, n) (28)

который называют методом Хьюна.

§6. Постановка задачи Коши для ОДУ n - го порядка.

Напомним, что в соответствии с определением, приведённым в начале данной лекции дифференциальным уравнением n -го порядка называется уравнение, связывающее одну независимую переменную x, функцию y (x) и её производные до порядка n – включительно y ¢(x), y ¢¢(x), …, y ^{( n )}(x).

Наивысший порядок входящих в уравнение производных неизвестной функции y (x) называется порядком дифференциального уравнения.

Дифференциальное уравнение называется обыкновенным, если неизвестная функция, входящая в это уравнение, является функцией одного переменного, в противном случае дифференциальное уравнение называется уравнением в частных производных.

Общий вид обыкновенного дифференциального уравнения n -го порядка представляют в виде неявной функциональной зависимости:

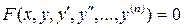(29)

Общим решением или интегралом ОДУ (1) является функция независимой переменной x и n - постоянных интегрирования С ₁, С ₂, …, С_n:

y = j (x, С ₁, С ₂, …, С_n).

Для определения постоянных интегрирования С ₁, С ₂, …, С_n с целью выделения из общего множества (т.е. из общего многопараметрического семейства) интегральных кривых единственной кривой, проходящей через заданную точку
М (x ₀, y ₀, y ₁, y ₂, …, y_{n- 1}) в пространстве решений R ^{n +1}, необходимо задать n дополнительных условий в виде значений производных искомой функции в точке x ₀ до порядка n - 1 включительно. Эти дополнительные условия называют начальными условиями:

(30)

Задача нахождения решения уравнения (29), удовлетворяющего n начальным условиям (30), называется задачей Коши для ОДУ n -го порядка (29).

Если старшая производная y ^{( n )}(x) искомой функции y (x), входящая в ОДУ (29), выражается явно через производные меньших порядков (такие ОДУ называются каноническими), то задача Коши будет иметь вид:

(31)

§7. Постановка задачи Коши для нормальных систем n - го порядка.

Система ОДУ называется нормальной, если каждое уравнение, входящее в систему, слева содержит производную первого порядка от соответствующей искомой функции, а правая часть зависит от независимой переменной x и n искомых функций y ₁(x), y ₂(x), y ₃(x),..., y _n (x):

(32)

Для того чтобы сформулировать задачу Коши для нормальной системы ОДУ (32), к системе (32) необходимо добавить n начальных условий (по количеству неизвестных функций), задаваемых в одной и той же точке x ₀:

(33)

Порядком нормальной системы (32) называют число уравнений в этой системе.

§8. Сведение задачи Коши для ОДУ n - го порядка к задаче Коши для системы ОДУ n - го порядка.

Одним из способов численного решения начальных задач для ОДУ высших порядков является сведение их к соответствующим задачам Коши для нормальных систем ОДУ дифференциальных уравнений того же порядка. Данный подход является следствием следующего общего утверждения:

Задачу Коши (31) для ОДУ n -го порядка всегда можно привести к задаче Коши (32), (33) для нормальной системы ОДУ того же порядка.

Общее доказательство данного утверждения вполне элементарно и не составляет труда [6, стр. 152 ], здесь проиллюстрируем его на примере задачи кроши для канонического ОДУ второго порядка.

Рассмотрим задачу Коши для ДУ второго порядка:

. (34)

(35)

отметим, что в этом случае задаётся начальное значения искомого решения и значение его первой производной .

Введя новую переменную z (x) = y ¢, от уравнения (34) переходим к эквивалентной ему системе уравнений:

(36)

Очевидно, что начальные условия для системы (36) перепишутся в виде:

(37)

Таким образом, задача Коши (34), (35) для уравнения второго порядка (34) сведена к системе (36) уравнений первого порядка с соответствующими начальными условиями (37).

В связи с этим в нашем курсе будут рассмотрены численные методы решения задач Коши для ОДУ первого порядка и задач Коши для нормальных систем ОДУ.

§9. Метод Эйлера для нормальных систем ОДУ.

Как известно задача Коши для ОДУ первого порядка имеет вид:

,

Если ввести на отрезке равномерную сетку x_i = x ₀ + ih, то вычислительная схема получения приближенного решения задачи Коши, порождаемая методом Эйлера, определяется соотношением:

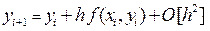, i = 0, 1, 2,… (38)

Адаптируем данный метод Эйлера для решения нормальных систем ОДУ второго порядка:

Выбирая шаг h численного интегрирования h = x_{i +1} - x_i, запишем алгоритм (38) отдельно для каждого уравнения системы ОДУ (39), (40) i = 0, 1, 2,…

, (43)

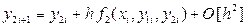, (44)

Выражения (43), (44) описывают алгоритм метода Эйлера для нормальной системы ОДУ (39) – (42)

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КОШИ

ПРИМЕР 1. Решить задачу Коши для линейного ДУ:

y ¢(x) = 2 x – 3 y; y (0) = 1;

т.е. необходимо найти решение данного ДУ, проходящее через точку (x ₀ = 0, y ₀ = 1).

На примере этой задачи Коши проследим за вычислениями, полученными при реализации различных представленных выше численных методов решения задачи Коши для ОДУ.

Поскольку для данного случая известно точное решение задачи Коши,

то это даёт возможность сравнить результаты приближённых вычислений, полученные при реализации различных рассмотренных выше схем численного решения и проверить насколько изложенные представления о их точности соответствуют полученным практическим результатам.

1. Метод последовательных приближений Пикара.

В данном случае итерационная формула поиска решения начальной задачи для ОДУ имеет вид:

Применительно к условиям данной задачи имеем:

, т.е.

Подставляя в это итерационное соотношение y ₀ = 1, для n = 0, 1, 2 последовательно получаем:

Полученные результаты удобно сравнить с точным решением данного ДУ:

если фигурирующую там экспоненту предварительно разложить в ряд Тейлора по степеням x, т.е. в окрестности точки x = 0:

f (x) = f (0) +

f (x) = ½ _{x = 0} = 1.

½ _{x = 0} = -3.

½ _{x = 0} = 9.

½ _{x = 0} = - 27.

½ _{x = 0} = 81.

В результате имеем: =

Сравнивая с точным решением полученные выше результаты видно что, приближения y ₁, y ₂, y ₃, полученные с использованием метода последовательных приближений Пикара хорошо согласуются с точным решением.

Далее проведём подсчёт приближённых значений решения y (x) данной задачи по методу Эйлера и его модификациям в точках x ₁ = 0.1, x ₂ = 0.2, т.е. с шагом h = 0.1; результаты сравнения найденных значений и фактические ошибки, найденные сравнением с точным значением y (0.2) = 0.581881 приведём в итоговой таблице 2.

2. Метод Эйлера.

В данном случае процесс отыскания таблицы решений, определяется следующей пошаговой последовательностью:

,

……………………………………………………………

Подставляя сюда величины h = 0.1; x ₁ = 0.1, x ₂ = 0.2, и начальное условие x ₀ = 0, y ₀ = 1, получим следующие приближённые значения для решения y (x) рассматриваемой задачи Коши: y¢ (x) = 2 x – 3 y; y (0) = 1.

;

;

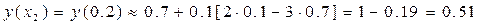3. Неявный метод Эйлера.

В данном случае процесс пошагового отыскания таблицы решений, определяется соотношениями:

,

……………………………………………………………

Подставляя сюда величины h = 0.1; x ₁ = 0.1, x ₂ = 0.2, и начальное условие x ₀ = 0, y ₀ = 1, получим следующие приближённые значения для решения y (x) рассматриваемой задачи Коши:

y¢ (x) = 2 x – 3 y; y (0) = 1.

;

.

0.6343;

4. Метод трапеций – модификация метода Эйлера.

В данном случае процесс пошагового отыскания таблицы решений, определяется соотношениями:

…………………………………………………………………………………

Подставляя сюда величины h = 0.1; x ₁ = 0.1, x ₂ = 0.2, и начальное условие x ₀ = 0, y ₀ = 1, получим следующие приближённые значения для решения y (x) рассматриваемой задачи Коши: y¢ (x) = 2 x – 3 y; y (0) = 1.

;

;

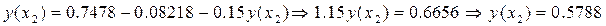5. Метод Хьюна – модификация метода Эйлера.

В данном случае процесс пошагового отыскания таблицы решений, определяется соотношениями:

……………………………………………………………………………………………………………………

Подставляя сюда величины h = 0.1; x ₁ = 0.1, x ₂ = 0.2, и начальное условие x ₀ = 0, y ₀ = 1, получим следующие приближённые значения для решения y (x) рассматриваемой задачи Коши: y¢ (x) = 2 x – 3 y; y (0) = 1.

Здесь при вычислении y (x ₁) по формуле:

мы воспользуемся результатом, полученным ранее в п. 2 при реализации метода Эйлера, т.е. учтём, что: ;

В этом случае при реализации вычислительной схемы для метода Хьюна, получаем:

;

Аналогично перед вычислением по формуле:

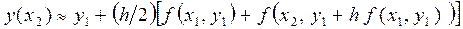
предварительно вычислим, что .

В результате для y¢ (x) = f (x, y) = 2 x – 3 y; h = 0.1; x ₁ = 0.1, x ₂ = 0.2, y ₁ = 0.755, окончательно имеем:

Таблица 2 -Сводные результаты решения задачи Коши по пунктам 1 - 5

Наименование метода	y 1 » y (0.1)	y 2 » y (0.2)	y (0.2) - y 2(истинное)
Метод Эйлера	0.7	0.51	0.07
Неявный метод Эйлера	0.7846	0.6343	- 0.05
Метод трапеций - Эйлера	0.7478	0.5788	0.003
Метод Хьюна	0.755	0.5895	- 0.008

Из таблицы 2 видно, что большей точностью обладают методы второго порядка, результаты которых представлены в двух последних строчках.

ПРИМЕР 2.

Методом Эйлера с шагом h = 0.1 численно проинтегрировать следующую задачу Коши для нормальной системы второго порядка до значения x = 0.2 включительно:

Для решения данной задачи Коши необходимо вычислить значения искомых функций y ₁(x) и y ₂(x) в узлах x ₀ = 0; x ₁ = 0.1 и x ₂ = 0.2 равномерной сетки с шагом h = 0.1; выполнив два шага по схеме Эйлера:

, (43)

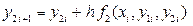, (44)

Очевидно, что для данного случая схема (43 - 44) будет переписана в виде:

(43)

(44)

Отсюда на первом шаге, при i = 0; x ₀ = 0; y ₁₀ = 1; y ₂₀ = 1 имеем:

Далее на втором шаге, при i = 1; x ₁ = 0.1; y ₁₁ = 1.3; y ₂₁ = 1.3 в соответствии со схемой (43 - 44) получим:

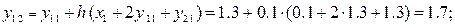
Для оценки качества полученного численного решения отметим, что данная задача Коши допускает точное (т.е. аналитическое) решение следующего вида:

и

откуда легко найти точные значения искомых решений y ₁(x) и y ₂(x) в заданных узлах

x ₀ = 0; x ₁ = 0.1 и x ₂ = 0.2:

и

Заключение (план - аннотация лекции №22).

В качестве справочного материала приведены основные определения теории дифференциальных уравнений и дана их геометрическая интерпретация. Дана формулировка начальной задачи (задачи Коши) для обыкновенного дифференциального уравнения первого порядка.

Обоснована необходимость разработки численных (приближённых) методов решения начальных задач для обыкновенных дифференциальных уравнений. Приведена постановка задачи численного решения задачи Коши и дана классификация приближенных методов решения начальных задач для обыкновенных ДУ. В зависимости от того, ищется ли приближенное решение в аналитическом виде или в виде таблицы чисел, приближенные методы поделены соответственно на аналитические и численные.

В виду того, что исходным моментом построения ряда численных схем решения начальных задач является преобразование исходной задачи Коши в интегральное уравнение, приведено доказательство теоремы об эквивалентности начальной задачи для ОДУ первого порядка соответствующему интегральному уравнению.

В качестве примера приближённо-аналитических методов решения задачи Коши для ОДУ первого порядка дан вывод метода последовательных приближений Пикара и приведены его вычислительные свойства.

Приведены геометрический и квадратурный вывод метода Эйлера, занимающего оду из ключевых позиций в ряду численных методов решения ОДУ. В качестве модификаций метода Эйлера рассмотрены методы:

– неявный метод Эйлера (модификация по методу прямоугольников);

– неявный метод трапеций (модификация по методу трапеций);

– метод Хьюна (комбинация метода Эйлера и неявного метода трапеций).

Дана постановка задачи Коши для ОДУ n -го порядка и нормальных систем n -го порядка. Рассмотрен метод Эйлера для нормальных систем ОДУ. Показан алгоритм сведения задачи Коши для ОДУ n -го порядка к задаче Коши для нормальной системы ОДУ соответствующего порядка.

Приведены примеры решения типовых задач.

Литература:

1. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002. – 840 стр.

2. Мастяева И.Н., Семенихина О.Н. Численные методы: Учебное пособие / Московский международный институт эконометрики, информатики, финансов и права. – М.: МЭСИ М., 2003. – 102 стр.

3. Л.Э. Эльсгольц. Дифференциальные уравнения и вариационное исчисление.
– М.: Наука, 1965. – 424 стр.

4. И.Г. Петровский. Лекции по теории обыкновенных дифференциальных уравнений. – М.: Наука, 1970. – 280 стр.

5. Приклонский В.И. Численные методы. Лекционный курс, читаемый в МГУ. Адрес в Интернете ttp://afrodita.phys.msu.ru/download/priklonsky/lections/

6. В.Ф. Формалёв, Д.Л. Ревизников. Численные методы. – М.: Физматлит, 2004. 400 с.