Аппроксимации производных в виде разностных отношений различного порядка точности на основе формулы Тейлора

3.1 Вводные замечания.

При получении простейших аппроксимаций производных в виде разностных отношений различного порядка точности предполагаем, что функция y = f (x) обладает гладкостью, необходимой для получения остаточных членов соответствующего порядка малости. При этом для наглядности будем пользоваться рис. 2.

При построении простейших аппроксимаций производных в виде разностных отношений пользуются следующей терминологией [2, стр. 514 - 515].

- аппроксимация производной f¢ (x_i) в узле x_i сетки, выраженная только через значения функции в узлах x _{i- 1}; x_i или только через значения функции в узлах x_i, x _{i+ 1}, называется несимметричной аппроксимацией.

- аппроксимация производной f¢ (x_i) в узле x_i сетки, выраженная через значения функции в узлах x_{i- 1}, x_i, x _{i+ 1}, называется симметричной аппроксимацией.

Рисунок - 2 построение простейших аппроксимаций производных

При выводе формул для простейших аппроксимаций производных мы будем использовать разложение функции y = f (x) в ряд Тейлора с остаточным членом в форме Лагранжа. Поэтому кратко напомним некоторые моменты, связанные с разложением функции в ряд Тейлора.

1. Пусть P_n (x) – полином степени n: P_n (x) = a ₀ + a ₁ x + a ₂ x ² +… + a_n xⁿ

тогда, как известно, его можно представить следующим рядом Тейлора [3, стр. 183]:

где x ₀ – некоторая фиксированная точка.

2. Если вместо полинома P_n (x) взять функцию y = f (x), которая в окрестности некоторой точки x ₀ (включая саму точку x ₀) имеет все производные до n- го порядка включительно, то в окрестности точки x ₀ функция f (x) представима рядом Тейлора [3, стр. 185 - 187]:

где с – некоторая точка, лежащая между точками x 0 и x: с Î(x 0, x).

(25)

В отличие от полинома P_n (x) степени n, выражение (25) для представления функции f (x) рядом Тейлора является точным, только при наличии в этом представлении слагаемого (остаточного члена):

, ~ о ((x - x ₀) ⁿ), при x ® x ₀.

который при постоянном n и при x ® x ₀ является величиной о ((x - x ₀) ⁿ), т.е. величиной бесконечно малой порядка выше n- го по сравнению с разностью (x - x ₀).

3.2 Аппроксимации первой производной.

Несимметричная аппроксимация f¢ (x) первого порядка точности.

Пусть дважды дифференцируемая функция y = f (x), задана на сетке равноотстоящих узлов с шагом h. Запишем данную функцию y = f (x) в виде ряда Тейлора в окрестности узла x_i с точностью до слагаемых второго порядка малости:

, где x Î(x; x_i).

Отсюда для f¢ (x_i), получим:

(26)

Выражение (26) является точным и выражает производную f¢ (x_i) функции f (x) в узле x_i через f (x_i) и значение f (x) в окрестности узла x_i.

Первым слагаемым правой части равенства (26) является разностное отношение, аппроксимирующее производную вблизи точки x_i, а второе слагаемое – это остаточный член (ошибка аппроксимации), характеризующий точность такой аппроксимации.

Зафиксируем в формуле (26) x = x_{i– 1}, при этом величина x = x _{i– 1} Î(x _{i– 1}; x_i). В этом случае получаем формулу левой аппроксимации производной f¢ (x_i):

(27)

Аналогично при x = x_{i+ 1}, x = x _{i+ 1} Î(x _i; x_{i+ 1}) и из формулы (26) получаем формулу правой аппроксимации производной f¢ (x_i):

(28)

При i = 1 и i = 0 из формул (27) и (28) соответственно получаем приближённые равенства:

, x₀ Î(x ₀; x ₁) (29)

, x₀ Î(x ₀; x ₁) (30)

Остаточные члены в формулах (29) и (30) указывают на то, что, пользуясь аппроксимацией (29), (30), мы совершаем ошибку, величина которой ведёт себя как о (h), т.е. эти аппроксимации первой производной имеют первый порядок точности.

Симметричная аппроксимация f¢ (x) второго порядка точности.

Пусть трижды дифференцируемая функция y = f (x), задана на сетке равноотстоящих узлов с шагом h. Запишем данную функцию y = f (x) в виде ряда Тейлора в окрестности узла x_i с точностью до слагаемых третьего порядка малости:

, где x Î(x; x_i).

При x = x _{i+ 1} и x = x _{i– 1} из предыдущего соотношения получим:

, x _{i+ 1}Î(x_i; x _{i+ 1})

, x _{i- 1}Î(x _{i– 1}; x _i)

Вычитая почленно второе равенство из первого, получим:

откуда Þ

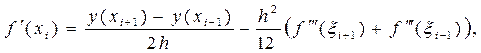или

(31)

Далее, считаем, что f¢¢¢ (x) является непрерывной на промежутке [ x _{i- 1}; x _{i+ 1}].
Поэтому, если f¢¢¢ (x _{i- 1}) и f¢¢¢ (x _{i+ 1}) значения функции f¢¢¢ (x) в некоторых точках промежутков (x_{i- 1}; x _i) и (x_i; x _{i+ 1}) соответственно, то на [ x _{i- 1}; x _{i+ 1}] функция f¢¢¢ (x) принимает и все промежуточные значения между величинами f¢¢¢ (x _{i- 1}) и f¢¢¢ (x _{i+ 1}), а значит, существует такая точка x _i Î(x_{i- 1}; x _{i+ 1}), где функция f¢¢¢ (x) равна:

(32).

Следовательно, используя в формуле (31) равенство (32), приходим к формуле симметричной аппроксимации f¢ (x_i) с остаточным членом второго порядка малости:

, x _i Î(x _{i- 1}; x _{i+ 1}). (33)

Полученная формула (33) симметричной аппроксимации f¢ (x_i) имеет второй порядок точности относительно шага h. При этом «основная» часть формулы (33)

при i = 1 совпадает с формулой (19):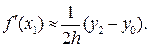

3.3 Аппроксимации второй производной.

a) Симметричная аппроксимация f ¢¢ (x) второго порядка точности.

Пусть достаточно гладкая функция y = f (x), задана на сетке равноотстоящих узлов с шагом h. Запишем представление функции y = f (x) рядом Тейлора в окрестности точки x_i с точностью до слагаемых четвёртого порядка малости:

, где x Î(x; x_i).

При x = x _{i+ 1} и x = x _{i- 1} из предыдущего соотношения получим:

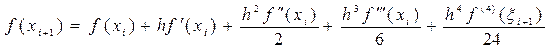, x _{i+ 1}Î(x_i; x_{i+ 1}).

, x _{i– 1}Î(x _{i– 1}; x_i).

Складывая почленно два последних равенства, получим:

(34)

Далее, считаем, что f ⁽⁴⁾(x) является непрерывной на промежутке [ x_{i– 1}; x_{i+ 1}]. Поэтому, если f ⁽⁴⁾(x _{i– 1}) и f ⁽⁴⁾(x _{i+ 1}) значения производной f ⁽⁴⁾(x) в некоторых точках смежных промежутков (x_{i– 1}; x_i) и (x_i; x_{i+ 1}) соответственно, то на [ x_{i– 1}; x_{i+ 1}] производная f ⁽⁴⁾(x) принимает и все промежуточные значения между величинами f ⁽⁴⁾(x _{i– 1}) и f ⁽⁴⁾(x _{i+ 1}), следовательно, существует такая точка x _i Î(x_{i– 1}; x_{i+ 1}), где производная f ⁽⁴⁾(x _{i– 1}) равна:

, следовательно,

, x _i Î(x_{i– 1}; x_{i+ 1})

Поэтому соотношение (34) можно переписать в виде:

(35)

Выражая из равенства (35) величину f¢¢ (x_i) приходим к формуле:

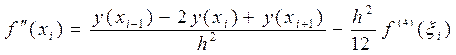, x _i Î(x_{i– 1}; x_{i+ 1}) (36)

Таким образом, формула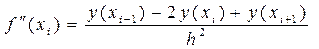

определяет симметричную аппроксимацию второго порядка точности для второй производной, погрешность которой определяется остаточным членом:
и является величиной о (h ²).

b) Несимметричная аппроксимация f ¢¢ (x) первого порядка точности.

Пусть достаточно гладкая функция y = f (x), задана на сетке равноотстоящих узлов с шагом h.

Покажем, что соотношение (36), используемое в качестве несимметричной аппроксимации для второй производной f¢¢ (x), т.е. для f¢¢ (x_{i+ 1}) или для f¢¢ (x_{i- 1}), является аппроксимацией первого порядка точности (а не второго).

Действительно, при всех необходимых оговорках о гладкости функции
y = f (x), в окрестности узла x_i вторую производную, т.е. функцию f¢¢ (x) также можно представить рядом Тейлора:

x Î(x; x_i) (37)

Подставляя в (37) вместо f¢¢ (x_i) правую часть равенства (36) получаем:

(38)

x _i Î(x_{i– 1}; x_{i+ 1}), x Î(x; x_i).

Из (38) при x = x_{i- 1} и x = x_{i+ 1} получаются следующие частные формулы для несимметричной аппроксимации второй производной:

, x _{i- 1} Î(x_{i- 1}; x_i) (39)

x _{i+ 1} Î(x_i; x_{i+ 1}) (40)

погрешности формул (39), (40) определяется выражениями:

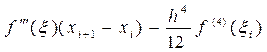, x _i Î(x_{i– 1}; x_{i+ 1}), x Î(x_i; x_{i+ 1}),

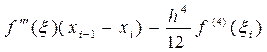, x _i Î(x_{i– 1}; x_{i+ 1}), x Î(x_{i- 1}; x_i),

и имеют порядок малости о (h).

§4. Погрешность формул численного дифференцирования.

При выводе формул численного дифференцирования исходную функцию
y = f (x) на интересующем интервале значений [ a, b ] заменяют интерполирующим полиномом P_n (x), а затем полагают, что при a £ x £ b f¢ (x) = P_n ¢(x). Аналогично поступают и при нахождении производных высших порядков.

Если для используемой интерполирующей функции P_n (x) известно выражение для ошибки (погрешности) интерполяции R (x) = f (x) - P_n (x), то, как отмечалось выше, погрешность аппроксимации производной выражается формулой:

R ¢(x) = [ f (x) - P_n (x) ]¢ = f¢ (x) - P_n ¢(x)

Считаем, что дифференцируемая функция y = f (x) задана своими значениями
y (x ₀), y (x ₁), y (x ₂), …, y (x_n), на сетке равноотстоящих узлов : x ₀, x ₁, x ₂, …, x_n отрезка [ a, b ], т.е. x_i = x ₀ + ih, где i = 1, 2, …, n, где h > 0 - шаг сетки.

Пусть далее на сетке узлов функцию y = f (x) заменяют первым интерполяционным полиномом Ньютона k – го порядка P_k (x) с базовым узлом x_i.

y (x)» P_k (x_i + qh) = y (x_i) + q D y_i + + + +

+…+ , .

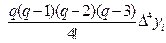В этом случае ошибка аппроксимации определяется выражением R_k (x) = f (x) - P_k (x), и, следовательно, для погрешности аппроксимации производной f¢ (x), которая обусловлена подменой функции f¢ (x) её интерполирующим полиномом P_k (x) имеем:

R¢_k (x) = f¢ (x) - P¢_k (x).

Как известно, погрешность первой интерполяционной формулы Ньютона определяется выражением:

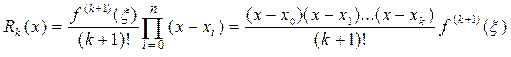(41)

где x - некоторая (вообще говоря, неизвестная, и, причём, зависящая от x) точка промежутка интерполяции (a, b).

Переходя в выражении (1) от переменной x к переменной имеем:

(42)

Напомним, что выражение (42) получено при условии, что f (x) Î , т.е. функция y = f (x) имеет на [ a, b ] все производные включительно. Поскольку мы получаем выражение для R¢_k (x), то необходимо дополнительно потребовать, чтобы на [ a, b ] функция f (x) имела уже все производные до включительно, т.е. чтобы f (x) Î . Поэтому из (42), полагая, что
f (x) Î и учитывая, что , получим:

(43)

Далее подставим значение базового узла x_i вместо переменной x в выражение (43). При x = x_i переменная , следовательно, сомножитель во втором слагаемом выражения (43) обращается в нуль. Поэтому если предположить, что является величиной ограниченной на [ a, b ], то можно считать, что при x = x_i

.

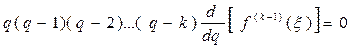Далее следует учесть, что , действительно

= .

Поэтому при q = 0 из последнего выражения получаем:

Таким образом, из (43) для значения погрешности производной в точке x = x_i получаем выражение:

(44)

Из выражения (44) следует, что для расчёта значения необходимо знать величину , которую трудно оценить, поскольку x - некоторая (вообще говоря, неизвестная, причём зависящая от x_i) точка промежутка интерполяции (a, b).

На практике для оценки величины пользуются связью между производными функции f (x) и её конечными разностями D ^{k+ 1} y_i соответствующих порядков, считая, что

D ^{k+ 1} y_i» f ^{( k+ 1)}(x_i)× h^{k+ 1}.

Поскольку в формуле (44) нам необходимо оценить величину , где x некоторое (заранее неизвестное и зависящее от x_i) промежуточное значение с интервала интерполяции (a, b), то вместо величины в формулу (44) подставляют значение:

или соответствующую ему величину 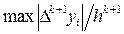, рассчитанную для i = 0, …, k. Следовательно, заменяя в формуле (44) величину на выражение:

(45)

окончательно имеем:

(46)

или

(47)

Аналогично может быть получено выражение и для оценки погрешности 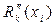аппроксимации второй производной .

Воспользуемся формулой (44) чтобы получить выражения для ошибок полученных выше несимметричных аппроксимаций первых производных:

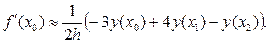(18)

(20)

Поскольку аппроксимации (18), (20) получены при интерполировании функции f (x) первым интерполяционным полиномом Ньютона второй степени (n = 2), построенным по трём точкам x ₀, x ₁, x ₂ (см. выше п. 2.3), то, полагая в формуле (44) k = 2, i = 0 и i = 2 получаем:

, x₀Î(x ₀, x ₂). (48)

, x₂Î(x ₀, x ₂). (49)

С учётом выражений (48), (49) формулы (18), (20) перепишем в окончательном и более общем виде.

, x _{i- 1}Î(x _{i- 1}, x _{i+ 1}) (50)

, x _{i+ 1}Î(x _{i- 1}, x _{i+ 1}) (51)

Заметим, что формулы (50), (51) для несимметричной аппроксимации f¢ (x_{i- 1}) и f¢ (x_{i+ 1}) второго порядка точности имеют в остаточном члене вдвое больший коэффициент, чем формула симметричной аппроксимации

, x _i Î(x _{i- 1}; x _{i+ 1}). (33)

т.е. (50), (51) имеют коэффициент вместо коэффициента в случае симметричной аппроксимации (33).