Применение критерия Стьюдента для сравнения генеральных совокупностей

Например, нам надо оценить эффективность действия рекламы какого-то товара. До запуска рекламы продажа товара по неделям (в шт.) имела следующий вид:

После выпуска рекламы продажа этого же товара по неделям стала иметь вид:

Следовательно, доверительный интервал с надежностью для первой выборки равен

А для второй

Таким образом, если по средним мы можем сделать положительный вывод о влиянии рекламы товара, то по доверительным интервалам мы вправе сомневаться: уж очень велики интервалы и они значительно перекрывают друг друга (см. рис. 5.3).

Однако нам необходимо со всей определенностью истолковать результаты эксперимента.

Мы можем высказать два предположения (статистические гипотезы).

1. Нулевая гипотеза. Между генеральными совокупностями с параметрами и , и разница равна нулю, т.е. . Следовательно, разница между выборочными средними возникла случайно, в процессе группировки данных.

2. Альтернативная гипотеза, т.е. противоположная.

Для проверки этих гипотез существуют специальные параметры, которые табулированы и приводятся в соответствующих справочниках.

В частности, если сравниваемые генеральные совокупности имеют нормальный закон распределения, то сравнение выборочных средних проводят с помощью или критерия Стьюдента:

.

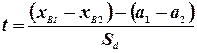
Согласно нулевой гипотезе , отсюда:

(5.9)

Нулевая гипотеза (разницы нет) отвергается, если для заданной надежности и числа (степеней свободы) . Здесь 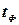- фактический коэффициент Стьюдента, найденный по формуле (5.9), а - теоретический коэффициент, найденный по специальным таблицам.

Для нашего примера , . Следовательно, . По таблицам, для надежности и числа , находим . Итак, и нулевая гипотеза сохраняется: разница между результатами опыта и контроля оказалась статистически недостоверной.

Таблица Стьюдента.

k	Уровни надежности
95 %	99 %	99,9 %
	2,37	3,50	5,51
	2,31	3,36	5,04
	2,26	3,25	4,78
	2,23	3,17	4,59