 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
I. Строительная теплофизика, теплотехника
|
|
1.1.  ;
; 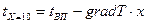 ;
; 
1.2. 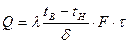

1.3. 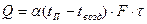
1.4.  ;
; 
1.5.  ;
; 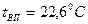 ;
; 
1.6. 

1.7.  ,
,  ,
, 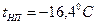 ,
,  ,
,  ,
,

1.8.  ;
; 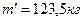 ;
;  ;
; 
1.9. -
1.10. 
1.11. 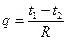
1.12. 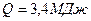
1.13. 
1.14. 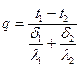
1.15. 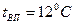 ;
; 
1.16.  ;
; 
1.17. 
1.18. 
1.19. 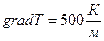 ;
; 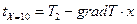 ;
; 
1.20. -
1.21.  ;
; 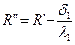
1.22.  ;
;  ;
; 

1.23.  ;
; 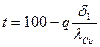
1.24. 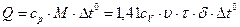
1.25. 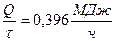
1.26. 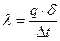
1.27. 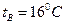
1.28..
 Введем обозначения: длина пластинок а, ширина с, толщины пластинок
Введем обозначения: длина пластинок а, ширина с, толщины пластинок 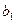 ;
;  ;
;  . Из уравнения Фурье
. Из уравнения Фурье 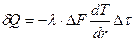 , преобразуем
, преобразуем 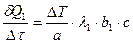 ;
;  ;
;  .
. 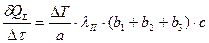 .
. 
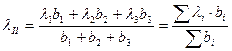
1.29.  ;
; 
1.30.  ;
; 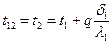 ;
; 
1.31.  ;
; 
1.32. 
1.33.  ;
;  ;
; 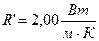
1.34. 
1.35. 
1.36. 
1.37. Считая режим стационарным можно записать:
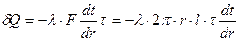 (1).
(1).
Разделяя переменные, получим  (2). Интегрируем выражение
(2). Интегрируем выражение
 (3).
(3).
При  ,
,  ;
; 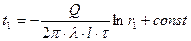 (4)
(4)
При  ,
,  ;
; 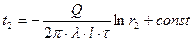 (5)
(5)
 (6) или
(6) или  (7). Закон распределения температуры
(7). Закон распределения температуры  : Из (4) определим значение const;
: Из (4) определим значение const; 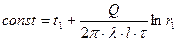 (8), а значение Q из (7) и подставим в (3).
(8), а значение Q из (7) и подставим в (3).
Получим 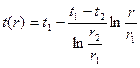 .
.
В инженерном деле вводят так же понятие  .
.
 это выражение более удобно при рассмотрении
это выражение более удобно при рассмотрении
задач теплопроводности многослойных стенок
1.38.  (1), разделяя переменные, получим
(1), разделяя переменные, получим 
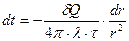 ;
;
следовательно 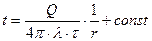 (2)
(2)
При  ,
,  тогда
тогда  (3).
(3).
При  ,
,  тогда
тогда 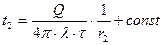 (4).
(4).
 (5). Выразим Q, получим
(5). Выразим Q, получим 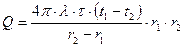 (6)
(6)
Выразим из уравнения (3) значение const: 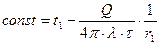 (7).
(7).
Подставим (6) и(7) в (3), получим значение  :
:
 . В инженерном деле вводят так же понятие плотности потока тепла через поверхность радиуса
. В инженерном деле вводят так же понятие плотности потока тепла через поверхность радиуса 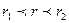

1.39. Температура поверхности льда практически совпадает с температурой воздуха. Пусть слой воды толщиной х замерз до льда, при этом выделилось тепло  . Удельная мощность теплового источника
. Удельная мощность теплового источника 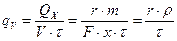 , при допущении, что толщина льда нарастает с постоянной скоростью. Уравнение Фурье для этого случая имеет вид
, при допущении, что толщина льда нарастает с постоянной скоростью. Уравнение Фурье для этого случая имеет вид  ;(1)
;(1)  (2)
(2)
Если  ,
,  ;
;  ,
,  . Подставим (2) в (1)
. Подставим (2) в (1) 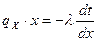 , разделяя переменные, получим
, разделяя переменные, получим 
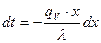 , следовательно
, следовательно  (3).
(3).
При  ,
, 
 ,
,  ,
, 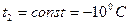
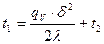
 ; подставляем значение
; подставляем значение 
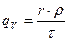 , получаем
, получаем 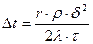 .
.
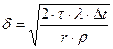 ;
;  .
.
1.40.  ;
; 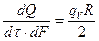
1.41. Увеличится на 
1.42.  ;
; 
Дата публикования: 2015-09-18; Прочитано: 325 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
