Источники опасности и повреждающие факторы

Источник опасности	Опасность (потенциальное чепе)	Повреждающий фактор
Сосуд с газом под давлением   Электрическая установка Подъемный кран Нагретый коллектор Ядерная установка Взрывоопасная смесь	Механический взрыв Утечка из сосуда Замыкание на корпус Обрыв троса Повреждение изоляции Вход в зону Химический взрыв	Летящие осколки Токсичный газ Электрический ток Движущийся груз Теплота Радиация Ударная волна

Следует отметить, что деление на источник, потенциальное чепе и повреждающий фактор производится в зависимости от тех задач, которые ставятся. Например, летящие осколки (см. табл. 4.4) можно при необходимости отнести к понятию источник опасности. Тогда потенциальным чепе может стать попадание осколков в человека, а повреждающим фактором — кинетическая энергия.

Чепе-несчастья создают повреждения, которые могут поддаваться или не поддаваться количественной оценке, например, смертельные случаи, уменьшение продолжительности жизни, вред здоровью, материальный ущерб, ущерб окружающей среде, неспокойное воздействие на общество, дезорганизация работы. Последствия или «количество нанесенного вреда» зависит от многих факторов, например, от числа людей, находившихся в опасной зоне, или количества и качества находившихся там материальных ценностей. С целью унификации различные последствия и вред обозначают термином ущерб. Ущерб измеряют денежным эквивалентом или числом летальных исходов, или количеством травмированных людей и т. п. Как это ни кощунственно, но между этими единицами измерения желательно найти эквивалент, чтобы ущерб можно было измерять в стоимостном выражении.

Техника вычисления вероятностей чепе. Через Р{Е} будем обозначать вероятность чепе Е^*. Вероятность достоверного события Р{1} = 1, вероятность невозможного события. Р{Æ} = 0, вероятность суммы попарно совместимых чепе (Е_iЕ_j = Æ, если i ≠ j) равна**

Рис. 4.4. Генерирование

полной группы событий

Когда число чепе превышает пять, картами Карт пользоваться неудобно. Тогда полную группу собы тий можно генерировать с помощью двоичных чисел. Делают это следующим образом. Для п чепе записывают десятичные числа от 0 до (2ⁿ - 1) и их пред ставления в двоичной системе счисления так, как этo сделано на рис. 4.4. Здесь, например, номер три дает набор 011, который соответствует чепе X* Y* Z.

На практике часто пользуются формулой объективной вероятности:

где п и n_E — соответственно общее число случаев и число случаев, при которых наступает чепе Е; при этом, если п не конечно, то оно должно быть достаточно большим (n ® ¥).

Определим вероятность чепе-несчастий. Н-чепе есть сумма

S=A+N (4.9)

Несчастный случай N и авария А могут наступать совместно. Поэтому формула (4.3) для определения вероятности P{S} не пригодна. Однако с помощью карты Карно (рис. 4.5) можно выделить полную группу событий: A̅N̅, AN̅, A̅N. AN. Тогда для аварии А= AN̅ + AN, несчастного случая N= NA̅ +AN и н-чепе S= N + А =AN̅ + NA̅ + AN можно записать:

P{A} = P{AN̅} + P{AN}, (4.10)

P{N} = P{A̅N} + P{AN}, (4.11)

P{S} =P[AN̅} + P{NA̅} + P{AN}. (4.12)

Из этих соотношений находим вероятность н-чепе:

Р{А + N} = Р{А} + P{N} — P{AN). (4.13)

Если катастрофа невозможна К= AN = Æ, то P[AN} = 0. формула (4.13) останется справедливой, если вместо чепе А и N в нее подставить любые другие события Х и Y. Заметим также, что при использовании понятия объективной вероятности (4.8) выражению (4.12) будет соответствовать соотношение

Рис 4.5. Вычисление вероятностей н-чепе с помощью карт Карно

Вероятность чепе Е₁ при условии E₂ обозначают Р{Е₁|Е₂}.Справедливы следующие соотношения (P{E₁} ≠0, P{E₂} ≠ 0):

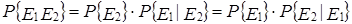(4.15)

Вычислим условную вероятность несчастного случая N при условии, что произошла авария А. Чтобы вычислить Р{N|А}, выделим на карте Карно (рис. 4.5, 6) только ту область, в которой осуществилось чепе А. Общее число случаев, в которых наступает авария А, равно n_A = n_AN̅ + n_AN. Тогда вероятность

( 4.16)

Если чепе E₁ и Е₂. независимые, т. е. если и , то

(4.17)

Распространяя эту.формулу на п взаимно независимых чепе E₁, E₂,…E_n получим

Если события нельзя считать независимыми, то справедливо более сложное выражение

Условные вероятности, входящие в выражение (4.19), эмпирически определить трудно или невозможно. Поэтому всегда стараются поставить задачу так, чтобы воспользоваться более простой формулой (4.18).