Частотные критерии устойчивости

Позволяют судить об устойчивости САР по виду ее ЧХ. Наиболее распространенные – критерии Михайлова, Найквиста. Более изящным является критерий Найквиста, который используется для исследования устойчивости замкнутых САР, судя о ней по виду известной ЧХ разомкнутой системы.

Все частотные критерии устойчивости базируются на принципе аргумента.

Принцип аргумента

Рассмотрим полином с действительными коэффициентами

,

имеющий n нулей, среди которых m являются правыми (имеют положительную вещественную часть), а остальные n–m – левыми.

Теорема. Приращение аргумента вектора при изменении частоты w от –¥ до +¥ равно разности между числом левых и правых нулей полинома , умноженной на p. т.е.

,

где – общее число нулей (равное порядку полинома ); – число правых нулей.

Доказательство. Разложим полином на множители:

и выполним подстановку :

.

Модуль этого вектора равен:

,

а аргумент –

. (*)

Каждый из элементарных векторов может быть изображен на комплексной плоскости в виде стрелки, выходящей из точки 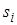и приходящей в точку . Пусть 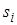– левый нуль полинома , а – правый. Их изображение на комплексной плоскости показано на рис.7.8.

Положительным направлением вращения есть вращение против часовой стрелки.

Из рис.7.8 видно, что изменяя w от –¥ до +¥, точка будет перемещаться вверх по мнимой оси, а аргумент вектора , соответствующего левому нулю, изменится от –p/2 до +p/2, т.е. на +p. Аналогично, аргумент вектора , соответствующего правому нулю, изменится от 3p/2 до p/2, т.е. на – p.

Таким образом, учитывая количество левых и правых нулей, из (*) получим:

.

Теорема доказана.

Следствие. Обычно рассматривают только положительные частоты, т.е. w изменяется от 0 до +¥. В этом случае приращение аргумента будет вдвое меньше и равно

.

Доказательство выполняется отдельно для действительных и комплексных нулей с учетом того, что последние в общем случае образуют комплексно-сопряженные пары.

Предварительные физические соображения

Считаем, что САР (рис.7.9) в разомкнутом состоянии устойчива (связь, проведенная пунктиром, отсутствует).

Частотная характеристика разомкнутой САР представлена на рис.7.10 (кривая 1).

Назовем частоту, при которой фазовый сдвиг равен , граничной (w_гр).

Изменим параметры САР таким образом, чтобы частотная характеристика разомкнутой системы прошла через точку с координатами (–1; j0). В этом случае коэффициент передачи при равен 1 (вне зависимости от амплитуды гармонического сигнала, т.е. вне зависимости от наличия или отсутствия обратной связи). Система не почувствует, если входной сигнал исчезнет, и в ней установятся незатухающие колебания. Говорят, что в этом случае система находится на границе устойчивости.

Если бы частотная характеристика разомкнутой САР не охватывала точку (–1; j0), как в случае 1 (рис.7.10), то коэффициент передачи при был бы меньше единицы, и колебания с течением времени затухли бы, т.е. САР в замкнутом состоянии была бы устойчивой.

В случае же, когда частотная характеристика разомкнутой САР охватывает точку (–1; j0), как в случае 2 (рис.7.10), коэффициент передачи при больше единицы, имели бы место расходящиеся колебания (с увеличивающейся амплитудой), т.е. САР была бы неустойчивой.

На основании физических соображений можно сделать вывод: Устойчивая в разомкнутом состоянии САР будет устойчива и в замкнутом состоянии, если частотная характеристика разомкнутой системы не охватывает точку с координатами (–1; j0).

Критерий устойчивости Найквиста (Nyqvist, 1932)

Пусть система в разомкнутом состоянии является неустойчивой. Обозначим:

– ПФ разомкнутой САР;

m – порядок неустойчивости разомкнутой САР, равный числу полюсов ПФ разомкнутой САР, находящихся в правой полуплоскости (если , то САР в разомкнутом состоянии устойчива).

Введем вспомогательную функцию:

,

где – характеристический полином разомкнутой САР;

– характеристический полином замкнутой САР.

Подставим :

.

Пусть характеристическое уравнение замкнутой САР имеет l правых корней. Тогда на основании принципа аргумента изменение угла поворота вектора при изменении частоты от 0 до +¥ будет равно:

.

Для устойчивости замкнутой САР необходимо и достаточно, чтобы все нули ее характеристического полинома были левыми, т.е. l=0. Тогда

.

Таким образом, если разомкнутая САР неустойчива и имеет m правых корней, то замкнутая САР будет устойчива тогда и только тогда, когда годограф вспомогательной функции при изменении частоты w от нуля до +¥ охватывает начало координат в положительном направлении m/2 раз.

Легко заметить, что число оборотов вектора вокруг начала координат равно числу оборотов вектора вокруг точки с координатами (–1; j0). Отсюда и вытекает общая формулировка критерия Найквиста.

Общая формулировка критерия. Для устойчивости замкнутой САР необходимо и достаточно, чтобы частотная характеристика разомкнутой САР с порядком неустойчивости m при изменении частоты w от нуля до + охватывала точку с координатами (–1; j0) в положительном направлении (при возрастании частоты) раз.

При сложной форме частотной характеристики бывает затруднительно определять число оборотов годографа вокруг критической точки (–1; j0). В этом случае удобно применять "правило переходов".

Положительным считается переход частотной характеристики через вещественную ось левее точки с координатами (–1; j0) при возрастании частоты w по направлению сверху вниз (рис.7.11). Отрицательным считается аналогичный переход, но по направлению снизу вверх (рис.7.11). Если частотная характеристика начинается или заканчивается на действительной оси левее точки с координатами (–1; j0), то говорят о ½-переходе (рис.7.11).

Формулировка, основанная на понятии переходов. Для устойчивости замкнутой САР необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов частотной характеристики левее точки с координатами (–1; j0) при изменении частоты w от нуля до +¥ была равна половине порядка неустойчивости разомкнутой САР m/2.

Например, замкнутая САР, имеющая в разомкнутом состоянии частотную характеристику 1 (рис.7.12), является неустойчивой, поскольку ЧХ охватывает точку с координатами (–1; j0) в отрицательном направлении, а замкнутая САР, соответствующая ЧХ 2 разомкнутой САР – устойчива, поскольку не охватывает точку с координатами (–1; j0).

Устойчивость астатических систем

Пусть имеется астатическая система -го порядка с ПФ разомкнутой САР

,

где – нормированная ПФ разомкнутой САР.

Частотная характеристика астатической САР

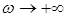стремится к нулю при (т.е. ЧХ заканчивается в начале координат), а при будет стремиться к бесконечности при угле (рис.7.13). Это обстоятельство приводит к неоднозначности использования критерия Найквиста.

Во избежание неопределенности частотные характеристики дополняются дугами длиной бесконечно большого радиуса (рис.7.13, пунктирные линии) и после этого анализируются дополненные ЧХ:

Замкнутая САР будет устойчивой, если ЧХ разомкнутой САР раз охватывает (или, если m=0) не охватывает точку с координатами (–1; j0) (рис.7.13).

Применение критерия Найквиста

к логарифмическим частотным характеристикам

Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) разомкнутой САР, как известно, вычисляется по формуле:

,

а логарифмическая фазо-частотная характеристика (ЛФЧХ) – по формуле

.

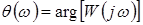Из ЧХ (рис.7.14) следует, что достижению частотной характеристикой окружности радиуса 1 с центром в начале координат при определенной частоте w_С, называемой частотой среза или граничной частотой, соответствует пересечение ЛАЧХ оси частот ().

Переходу годографа через вещественную ось при соответствует переход ЛФЧХ через отметку (В более сложных случаях, когда ЧХ имеет вид спирали – через отметки , , , …). При этом положительному переходу соответствует переход ЛФЧХ снизу вверх, а отрицательному переходу – сверху вниз.

Поэтому на основании критерия Найквиста может быть сформулирован:

Логарифмический частотный критерий устойчивости. Для устойчивости замкнутой САР необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов ЛФЧХ разомкнутой САР через линию (где k = 0, 1, 2, …) при частотах, когда , была равна .

Запас устойчивости

Вид частотной характеристики , как мы знаем, зависит от параметров разомкнутой САР. Путем изменения параметров САР (например, изображенной на рис.7.14) можно из области устойчивости перевести ее в область неустойчивости, и наоборот. Количественные параметры (т.е. степень) изменения параметров устойчивой (функционирующей) САР, необходимые для перевода ее на границу устойчивости (когда ЧХ проходит через точку с координатами (–1; j0)) характеризуют запас устойчивости САР.

Наиболее удобно количественное выражение запаса устойчивости может быть определено с помощью логарифмических частотных характеристик (ЛАЧХ и ЛФЧХ), причем различают запас устойчивости по амплитуде (определяемый по ЛАЧХ) и запас устойчивости по фазе (определяемый по ЛФЧХ).

Пусть имеется разомкнутая САР, логарифмические частотные характеристики которой приведены на рис.7.15.

Параметр A называется запасом устойчивости по амплитуде, определяется как отклонение ЛАЧХ от оси частот при частоте, соответствующей первому отрицательному переходу ЛФЧХ через уровень –p:

.

Предположим, что путем изменения параметров САР (путем увеличения коэффициента передачи) ее ЛАЧХ поднялась на величину A, и пусть при этом ЛФЧХ осталась без изменения. В этом случае САР находится на границе устойчивости.

Параметр y называется запасом устойчивости по фазе, определяется как отклонение ЛФЧХ от уровня –p при значении частоты w, равном частоте среза w_С:

.

Предположим, что также путем изменения параметров САР (путем установки фильтра с коэффициентом передачи, равном 1) ее ЛФЧХ опустилась на угол y, а ЛАЧХ осталась без изменения. И теперь САР находится на границе устойчивости.

В реальных САР в процессе работы под действием внешних факторов их параметры изменяются. При этом изменяются их ЛАЧХ и ЛФЧХ.

Для того, чтобы обеспечить нормальную (устойчивую) работу САР, обычно необходимо обеспечить запас устойчивости по амплитуде

дБ

и запас устойчивости по фазе

.

При невыполнении этих условий в процессе работы системы имеется большая вероятность того, что она окажется неустойчивой.

Пример 1. Исследовать на устойчивость САР, структурная схема которой представлена на рис.7.16.

Решение с помощью критерия устойчивости Гурвица.

ПФ разомкнутой САР:

.

Характеристический полином замкнутой САР:

,

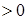т.е. 0,1 , 1,1, , .

Составляем матрицу Гурвица:

.

Находим определители:

; – САР неустойчива.

Решение с помощью логарифмического частотного критерия.

Строим ЛАЧХ и ЛФЧХ разомкнутой САР (рис.7.17). Имеем один отрицательный переход ЛФЧХ через уровень –p, а положительные переходы отсутствуют, т.е. разность между числом положительных и отрицательных переходов равна –1. Характеристический полином разомкнутой САР не имеет правых корней. Таким образом, логарифмический критерий не выполняется: 0 ¹ –1.

Кроме того, из ЛАЧХ и ЛФЧХ также видно, что САР имеет отрицательный запас устойчивости как по амплитуде, так и по фазе. Уже по этому мог бы быть сделан вывод о неустойчивости замкнутой САР.

Пример 2. Исследовать на устойчивость САР, структурная схема которой представлена на рис.7.18, с помощью логарифмического частотного критерия устойчивости.

Решение. Преобразовав структурную схему путем свертки внутреннего замкнутого контура, запишем ПФ разомкнутой САР:

.

Строим ЛАЧХ и ЛФЧХ разомкнутой САР (рис.7.19).

Очевидно, ЛФЧХ при частотах, меньших частоты среза, не пересекает уровень –p. Характеристический полином разомкнутой САР не имеет правых корней. Поэтому критерий устойчивости выполняется – замкнутая САР устойчива.

Отметим, что САР будет иметь недостаточный запас устойчивости по фазе.