Введение. Метод наименьших квадратов был предложен Гауссом и Лежандром в конце XVIII – начале XIX века связи с проблемой обработки экспериментальных данных

Метод наименьших квадратов был предложен Гауссом и Лежандром в конце XVIII – начале XIX века связи с проблемой обработки экспериментальных данных.

В этом случае задача построения функции непрерывного аргумента по дискретной информации , 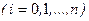характеризуется двумя особенностями.

1. Число точек , в которых производятся измерения, обычно бывает достаточно большим.

2. Значения функции в точках сетки определяются приближенно с неизбежными ошибками измерения.

С учетом этих обстоятельств строить функцию в виде полинома высокой степени и добиваться ее точного равенства в точках сетки величинам , как это делалось при интерполировании, становится нецелесообразным.

В методе наименьших квадратов аппроксимирующая функция ищется в виде полинома невысокой степени

, ,

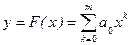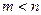в частности, возможен вариант, когда .