Сложные зубчатые механизмы

6.1. Общие сведения о сложных зубчатых механизмах

Различают одноступенчатые и многоступенчатые зубчатые механизмы.

Одноступенчатым называют такой зубчатый механизм, который не может быть расчленен на более простые.

Передаточное отношение одноступенчатого механизма целесообразно принимать не более 6...8. Иначе возрастают габариты колеса и всего механизма, происходит неравномерный износ колеса (шестерня изнашивается быстрее).

Многоступенчатые (сложные) зубчатые механизмы используют для получения больших передаточных отношений. Они образуются путем соединения нескольких одноступенчатых механизмов. Механизмы, понижающие угловую скорость, называются редукторами, повышающие – мультипликаторами.

Классификация сложных зубчатых механизмов

Все сложные зубчатые механизмы можно классифицировать по характеру движения и подвижности осей валов, а также по величине передаточного отношения.

а) классификация по характеру движения (подвижности) осей валов:

б) классификация по величине передаточного отношения U:

		Мультипликаторы (повышающие передачи). Направления вращения входного и выходного вала совпадают.
			Редукторы, уменьшающие величину угловой скорости и не изменяющие направления вращения
		Редукторы, уменьшающие величину угловой скорости и изменяющие направление вращения входного и выходного валов

6.2. Передачи с неподвижными осями колес

Рядовой зубчатый механизм – это последовательно соединенные несколько ступеней зубчатых колес. (рис. 6.1.).

Рис.6.1. Рядовой зубчатый механизм

Согласно определению, передаточное отношение равно отношению угловых скоростей входного и выходного валов , а передаточные отношения ступеней ; ; .

Перемножим левые и правые части этих выражений и приравняем их друг к другу:

.

Отсюда можно записать обобщенную формулу вычисления передаточного отношения

(6.1),

где n – количество валов, k – количество ступеней.

Так как , то формула расчета общего передаточного отношения рядового механизма выглядит так: .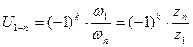

Отсюда следует, что его величина зависит только от количества зубьев входного и выходного колес. Промежуточные колеса служат лишь для увеличения межосевого расстояния и изменения направления вращения.

Ступенчатый механизм

Передаточное отношение ступенчатого зубчатого механизма рассчитывается по формуле (6.1).

Рис. 6.2. Ступенчатый зубчатый механизм

Для механизма, изображенного на рис. 6.2, формула расчета передаточного отношения выглядит так:

.

Ступенчатые механизмы применяются для:

- того же, что и рядовые, т.е. для изменения направления вращения выходного вала по отношению ко входному,

- получения больших передаточных отношений.

Например, с помощью 2х-ступенчатого механизма можно получить , 3х-ступенчатого - , 4х-ступенчатого - .

6.3. Планетарные передачи.

Различают 4 основных типа планетарных ступеней (так называемых механизмов Давида) (рис.6.3, схемы І - ІV):

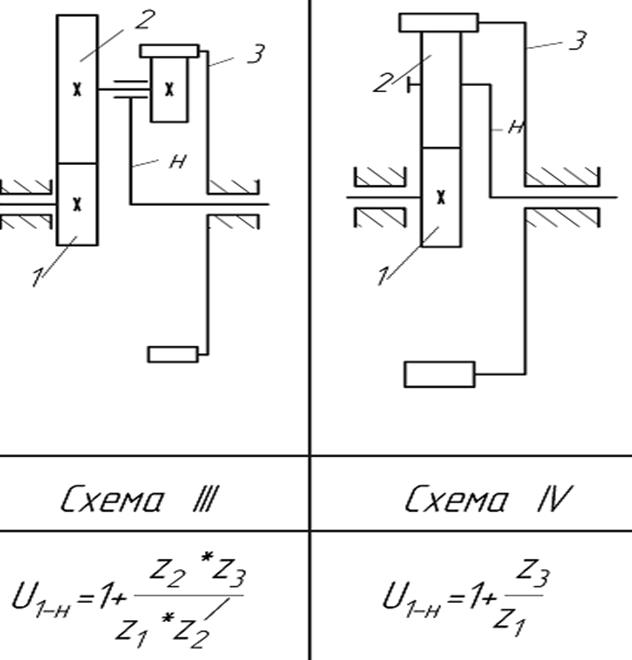
Рис.6.3. Кинематические схемы планетарных передач

Условные обозначения звеньев планетарных механизмов на рис. 6.3: 1 – центральное колесо, 2 – сателлиты, 3 – опорное (неподвижное) колесо; H – водило (от заглавной буквы слова Hedel – рычаг).

Преимущества планетарных передач:

- компактность при больших передаточных отношениях U;

- возможность передачи больших крутящих моментов (т.к. при их передаче используется несколько сателлитов);

Недостатки планетарных передач:

- сложность изготовления;

- требуются высокая точность изготовления и сборки.

6.3.1. Вычисление передаточного отношения планетарной передачи

Аналитический метод. Используем метод обращения движения – т.е. всему механизму, в том числе неподвижному колесу, условно придается (сообщается) угловая скорость - (то есть все звенья в таком механизме уменьшают скорость на величину угловой скорости водила ). Тогда в этом так называемом обращенном механизме водило H станет неподвижным, и мы получим простой ступенчатый механизм с неподвижными осями. Угловые скорости исходного планетарного и обращенного механизма сведем в таблицу:

№№ звеньев	Угловые скорости
В планетарном механизме	В обращенном механизме
H

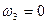
Вычисляем передаточные отношения обращенного механизма (на примере схемы I):

через угловые скорости (6.2)

через числа зубьев колес (6.3)

Из уравнений (6.2) и (6.3) получим:

Для других схем планетарных механизмов (рис. 6.3) выводы формул расчета передаточных отношений аналогично предыдущему.

Общая формула имеет вид

,

где - передаточное отношение обращенного механизма.

Графический метод расчета передаточного отношения планетарной передачи заключается в том, что сначала строят кинематическую схему механизма в масштабе, затем картину (план) линейных скоростей и картину угловых скоростей. Используя геометрические размеры построений, вычисляют передаточное отношение. Рассмотрим последовательность решения на примере механизма, изображенного на рис. 6.4.

Рис. 6.4. План механизма (а), картина линейных скоростей (б) и план угловых скоростей (в)

Последовательность решения

Строится кинематическая схема планетарного механизма в двух проекциях в выбранном масштабе (рис.6.4а). Для этого рекомендуется радиусы зубчатых колес (в мм) на схеме принимать равными числам зубьев (т.е. условно принимать модуль m = 2).

Строится план окружных линейных скоростей механизма в следующей последовательности. Из полюса зацепления 1 и 2 колес (точки Р₁₂ на правой проекции механизма) проводят вектор V_P12 произвольной длины. Он изображает линейную скорость точки P₁₂. Соединив конец этого вектора с точкой O₁, получают треугольник скоростей колеса 1. Здесь гипотенуза изображает изменение линейных скоростей колеса 1 от оси вращения до делительной окружности.

Строится треугольник скоростей звена 2. Для этого конец вектора V_P12 соединяют с неподвижным полюсом P₂₃ зацепления колес 2 и 3.

Строится треугольник скоростей водила Н. Для этого из точки O₂ проводят вектор линейной скорости V₀₂ до гипотенузы (прямой между точками P₂₃ и V_P12) треугольника скоростей сателлита 2. Соединив конец вектора V_O2 с точкой О_H гипотенузой, получают треугольник скоростей водила Н.

Как известно, величина передаточного отношения механизма равна отношению угловых скоростей (U_1-H = w₁/w_Н). Величины угловых скоростей 1-го колеса w₁ и водила w_Н пропорциональны тангенсам углов a₁ и a_Н на плане окружных линейных скоростей. Но так как углами при расчетах пользоваться не совсем удобно, то строится план частот вращения. Для этого проводят вертикальный отрезок ОР произвольной длины. Через точку О проводят горизонтальную линию. Из точки Р проводят под углами a₁, a₂, a_Н к отрезку ОР линии Р1, Р2 и РН, параллельные гипотенузам треугольников окружных скоростей. Отрезки Р1, Р2 и РН пропорциональны частотам вращения звеньев I, 2 и Н. Для вычисления передаточных отношений достаточно измерить длины этих отрезков и подставить в нижеприведенные формулы. Причем, если соотносимые отрезки лежат по одну сторону от точки О, то передаточное отношение берется со знаком плюс, если по разные – со знаком минус:

U^гр_1-Н = О1/ОН, U^гр₁₂ = - О1/О2.

При этих построениях принимается, что окружная линейная скорость точки А, принадлежащей колесу 1, равна

,

скорость точки О₂, принадлежащей сателлиту, равна

,

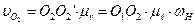угловая скорость центрального колеса 1, равна

,

угловая скорость водила Н

,

а величина передаточного отношения от колеса 1 к водилу Н будет равна

6.3.2. Геометрический синтез планетарных передач

Для создания работоспособной ступени планетарного механизма необходимо соблюдать три условия: соосности, соседства, собираемости.

Условие соосности

Оно обеспечивает достаточное и постоянное межцентровое расстояние между колесами.

Для схемы I (рис. 6.3) межосевые расстояния между осями валов 1 и 2, а также осями 2 и 3 равны:

или , откуда

Для схемы II это условие выглядит так:

Для схемы III:

Для схемы IV: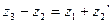

Условие соседства

Оно обеспечивает размещение на одной окружности нескольких сателлитных колес с некоторым зазором между ними (рис. 6.5).

Пусть K – количество сателлитов. Условие соседства можно выразить неравенством

,

где - радиус окружности выступов сателлита.

Рис. 6.5. Размещение соседних сателлитов планетарной передачи.

Так как , , то , или

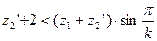. (6.4)

Неравенство (6.4) и представляет собой условие соседства.

Условие собираемости

Оно обеспечивает возможность зацепления всех сателлитных колес с центральными колесами при постоянстве угла между сателлитами. То есть при этом следует обеспечить такое условие, чтобы колеса вошли в зацепление строго в точках В и В’,D и D’ (рис. 6.5). Для вывода условия собираемости рассудим следующим образом. Пусть колесо 1 повернется на угловой шаг .

Так как , то водило повернется на угол

.

В пределах угла 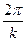угол 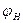должен располагаться целое число раз, т.е. , где C – целое число. Так как , то

. (6.5)

Равенство (6.5) и представляет собой условие собираемости планетарной передачи.

6.4. Дифференциальные механизмы.

Дифференциальные служат для разложения или сложения движения. Степень подвижности их . Например, если звено 3 (рис. 6.3, схема I) планетарного механизма сделать подвижным (дать ему возможность вращаться), то число низших кинематических пар будет равно 4 (они образованы звеньями 0 и 1, 2 и H, H и 3, 3 и 0), а число высших кинематических пар будет равно 2 (они образованы звеньями 1 и 2, 2 и 3). Количество подвижных звеньев n равно 4 (это звенья 1,2,3 и H). Тогда .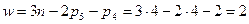

Если ведущим является центральное колесо 1, то мощность с него будет передаваться и распределяться на два звена одновременно – на водило H и колесо 3, которые и будут выходными. И наоборот, любые два из этих звеньев, будучи ведущими, могут передавать мощность на одно ведомое.

6.5. Пространственные зубчатые передачи

Коническая передача

Рис. 6.6. Геометрические параметры конической передачи.

Коническая передача как бы образована качением двух конусов ОР₁Р и ОР₂Р. Они называются начальными конусами. В точке Р окружные скорости обоих конусов равны: ; или ; . Отсюда передаточное отношение конической передачи имеет выражение: .

Для расчета геометрических параметров конических зубчатых колес используют те же формулы, что и для цилиндрических, вводя понятия эквивалентных цилиндрических колес. Для них числа зубьев:

; .

Различают следующие геометрические параметры конических зубчатых колес (рис. 6.7.)

делительная окружность ;

основная окружность ;

окружность выступов ;

окружность впадин ;

высота головки зуба ;

высота ножки зуба ;

конусное расстояние ;

ширина колеса .

Рис. 6.7. Основные геометрические параметры конического колеса.

Достоинства конической передачи:

- возможность передачи вращательного движения между осями под различными углами;

- больший коэффициент перекрытия, чем у цилиндрической (см. размеры эквивалентной цилиндрической передачи, у которой радиусы колес больше, чем у конической, а, значит, и возрастает величина практической линии зацепления ab).

Недостатки конической передачи:

- сложность изготовления зубчатых колес (по сравнению с цилиндрическими);

- повышенная чувствительность к изменению конусного расстояния;

- пониженная нагрузочная способность по сравнению с цилиндрической из-за консольного расположения одного из колес и несимметричного расположения второго относительно опор.

Гиперболоидные передачи

Гиперболоидные передачи образуются условным качением двух гиперболоидов (рис. 6.8).

Рис. 6.8. Принципиальные схемы отдельных разновидностей гиперболоидных передач.

Червячная передача (рис. 6.9) является одной из разновидностей винтовой передачи. Причем чаще всего угол между осями =90⁰.

Рис. 6.9. Кинематическая схема червячной передачи.

Как правило, ведущим звеном является червяк. Передаточное отношение при этом равно

,

где - число зубьев колеса,

- число заходов червяка.

Величина передаточного отношения может составлять U_Ч-К =10…100, что дает преимущество по сравнению с другими зубчатыми передачами. В общем виде у винтовой передачи передаточное отношение равно:

.

Недостатком гиперболоидных передач является невысокий механический КПД. В ряде случаев для его увеличения используют разные материалы, из которых изготовлены зубчатые колеса или их венцы. Это снижает коэффициент трения скольжения в месте контакта зубьев. Например, в червячной передаче червяк изготавливают из стали или чугуна, а венец зубчатого колеса – из бронзы.