Псевдовекторы

Псевдо (от др.-греч. ψεῦδος — ложь): Приставка, означающая ложность, ненастоящесть следующего за ней. Пример: псевдонаука.

В данном разделе используются некоторые сведения из теории определителей и векторной алгебры.

· Произведение определителей одного порядка можно преобразовать по формуле .

· Смешанное произведение следующим образом выражается через координаты векторов:

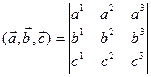
Если векторы заданы координатами относительно правой декартовой системы координат, то смешанное произведение, вычисленное по этой формуле равно объёму параллелепипеда, построенного на векторах 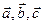, со знаком плюс, если тройка векторов правая, и со знаком минус, если она левая:

(Если векторы заданы координатами относительно произвольного базиса, то при изменении базиса значение может изменяться не только по знаку, но и по абсолютной величине; это значение зависит также от того, контравариантные или ковариантные координаты векторов использованы).

· Пусть векторы заданы координатами относительно правой декартовой системы координат. Тогда при помощи правила умножения определителей можно доказать,
что
.

Определение псевдотензора.

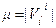Пусть заданы старый базис и новый базис . Определитель называется определителем перехода к новому базису.

Псевдовектором ранга веса называется объект, координаты которого перенумерованы индексами и при переходе к новому базису преобразуются как координаты тензора с дополнительным умножением на .

Например, координаты псевдовектора веса преобразуются по формулам .

Псевдовектор ранга называется псевдоскаляром, ранга 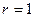– псевдовектором.

Псевдовектор веса является обычным (истинным, абсолютным) тензором.

Геометрический смысл определителя .

Определитель 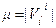равен отношению объёма параллелепипеда, построенного на векторах 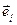, к объёму параллелепипеда, построенного на векторах (объёмы определяются по величине и знаку): .

Действительно, пусть векторы , 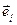заданы координатами относительно правой декартовой системы координат. Тогда, ,

Но .

(При выводе использованы равенства )

Следовательно, .

.

Если оба базиса , 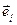– ортогональные, нормированные, то ; при этом , если тройки векторов обе правые или обе левые, в противном случае.

Вес произведения псевдотензоров.

Умножение псевдотензоров производится так же, как умножение тензоров. При этом вес произведения равен сумме весов сомножителей.

Пусть, например, – псевдоскаляр веса , а 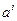– псевдовектор веса .

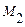Тогда

Как следствие, произведение истинного тензора на псевдотензор есть псевдотензор, произведение двух псевдотензоров с весами, равными по абсолютной величине и противоположными по знаку есть истинный тензор.

Псевдотензоры нужны для того, чтобы образовывать инвариантные векторы и скаляры.

Для этого используют несколько рассмотренных ниже псевдотензоров.

Примеры псевдотензоров.

1. Псевдоскаляр – объём параллелепипеда, построенного на векторах базиса (векторы заданы координатами относительно декартовой прямоугольной системы координат). По доказанному выше, , т.е. . Следовательно, вес псевдоскаляра равен 1.

Если известен метрический тензор 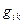, то псевдоскаляр можно выразить через его координаты.
Действительно,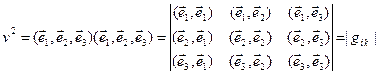

Введём обозначение . Тогда ; корню приписывают знак плюс, если тройка векторов правая, и знак минус, если она левая.

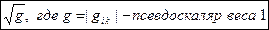
2. Псевдоскаляр . Вес псевдоскаляра равен– 1.

Действительно, .

3. .(символ Леви-Чивита) – ковариантный псевдотензор ранга 3 веса «– 1».

.

По определению координаты данного объекта имеют относительно любого базиса следующие значения:

Для доказательства псевдотензорного характера объекта с весом – 1 нужно проверить справедливость равенства .Проверим его, например, для .

По определению,

При этом

Равенство принимает вид .

Аналогичным образом можно проверить равенство для всех перестановок из индексов .

Равенство справедливо и в том случае, когда среди индексов 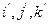есть равные, так как тогда полученный определитель третьего порядка равен нулю.

4. .(символ Леви-Чивита) – контравариантный псевдотензор ранга 3 веса «+ 1».

Для доказательства нужно использовать значение определителя .

Так как , по правилу умножения определителей получаем , или , откуда следует, что .

5. Псевдоскаляр , где – произвольные векторы.

Вес псевдоскаляра равен – 1, так как вес символа равен – 1, а веса векторов равны нулю.

Заметим, что есть истинный скаляр (инвариант), так как сумма весов псевдоскаляра и псевдотензора 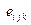равна нулю.

В развёрнутом виде .

Значение , вычисленное по этой формуле, не зависит от системы координат. В правой декартовой системе координат, для которой , оно равно объёму параллелепипеда, построенного на векторах 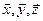, определённому по величине и знаку. Следовательно, получена формула для вычисления объёма параллелепипеда в системе координат с произвольным координатным базисом.

6. Контравариантный псевдовектор .

Вес псевдовектора равен 1. Следовательно, ест полярный (истинный) вектор.

В разложении по векторам базиса этот вектор имеет вид .

В развёрнутом виде:

Таким образом, .

Вектор не зависит от системы координат. В правой декартовой системе координат формула определяет вектор, равный по модулю площади параллелограмма, построенного на векторах , перпендикулярный к , направленный по правилу правого винта.

Полученная формула находит в системе координат с произвольным базисом.

Векторное произведение находится по формуле

.

Векторное произведение, которое находится по этой формуле, является псевдовектором веса 1, так как , где – полярный вектор, – псевдовектор веса 1.

Используя векторное произведение, можно представить в виде .