Вынужденные электромагнитные колебания

Вынужденными колебаниями называют такие колебания, которые вызываются действием на систему внешних сил, периодически изменяющихся с течением времени. В случае электромагнитных колебаний такой внешней силой является периодически изменяющаяся э.д.с. источника тока.

Отличительные особенности вынужденных колебаний: вынужденные колебания - незатухающие колебания; частота вынужденных колебаний равна частоте внешнего периодического воздействия на колебательную систему, т.е., в данном случае, равна частоте изменения э.д.с. источника тока.

Амплитуда вынужденных колебаний зависит от частоты изменения э.д.с. источника тока. Для вынужденных колебаний характерно явление электрического резонанса, при котором амплитуда вынужденных колебаний становится максимальной. Это физическое явление наблюдается при совпадении частоты изменения э.д.с. источника тока с собственной частотой колебаний данного контура, т.е.:

, (1)

где: i - мгновенное значение тока, т.е. его значение в момент времени t = 0;

J0 - амплитудное или максимальное значение силы тока;

w - частота изменения тока, численно равная частоте изменения э.д.с. источника тока.

Амперметры и вольтметры в цепи переменного тока измеряют так называемые действующие или эффективные значения переменного тока, которые связаны с амплитудными значениями тока по формулам:

, (4)

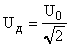. (5)

Действующими значениями силы тока и напряжения переменного тока называют значения этих величин для такого постоянного тока, который на том же активном сопротивлении выделяет за время, равное периоду Т переменного тока, такое же количество теплоты, как и данный переменный ток.

Источником переменного тока является генератор переменного тока, физический принцип действия которого основан на равномерном вращении с угловой скоростью w плоской рамки площадью S, состоящей из N витков, в однородном магнитном поле с индукцией В. При этом рамку пронизывает переменный магнитный поток:

, (6)

где: Ф0 - максимальное значение магнитного потока;

a - угол между нормалью к рамке и вектором магнитной индукции В;

w - угловая скорость вращения рамки.

Согласно закону электромагнитной индукции, в рамке будет возбуждаться мгновенное значение э.д.с., изменяющееся по закону:

, (7)

где: e - мгновенное значение э.д.с.;

e0 - амплитудное значение э.д.с.;

w - угловая скорость вращения рамки.

В общем случае цепь переменного тока представляет собой колебательный контур:

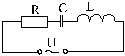
Напряжение на зажимах источника тока U меняется по гармоническому закону с частотой изменения э.д.с. генератора переменного тока.

Устройства, в которых электрическая энергия полностью и необратимо преобразуется в другие виды энергии, называют активными нагрузками, а электрические сопротивления этих устройств - активными сопротивлениями. В цепи постоянного тока существуют только активные нагрузки.

Устройства, в которых не происходит необратимого превращения электрической энергии в другие виды энергии, называют реактивными нагрузками, а их сопротивления - реактивными сопротивлениями. Реактивные сопротивления в цепи переменного тока имеют конденсатор и катушка индуктивности, которые соответственно называют емкостным xc сопротивлением и индуктивным сопротивлением xL. При этом конденсатор имеет только реактивное сопротивление, а катушка индуктивности, помимо реактивного сопротивления, обладает еще активным сопротивлением. Реактивные сопротивления вычисляются по формулам:

, (8)

, (9)

где: С - емкость конденсатора;

L - индуктивность катушки;

w - частота изменения э.д.с. источника тока.

Если в цепи переменного тока реактивной нагрузки нет или ее сопротивление пренебрежимо мало по сравнению с активным сопротивлением цепи, то колебания силы тока совпадают по фазе с колебаниями напряжения и происходят с частотой и фазой колебаний э.д.с. источника тока:

, (10)

, (11)

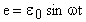. (12)

Цепь переменного тока, которая не содержит конденсатора и активное сопротивление которой ничтожно мало по сравнению с индуктивным сопротивлением, называется цепью переменного тока с индуктивным сопротивлением. В такой цепи колебания напряжения на катушке опережает колебания силы тока на π/2, т.е.:

, (13)

. (14)

Цепь переменного тока, которая не имеет индуктивного сопротивления и активное сопротивление которой пренебрежимо мало по сравнению с емкостным сопротивлением, называется цепью переменного тока с емкостным сопротивлением. В такой цепи колебания силы тока опережают колебания напряжения на π/2:

, (15)

. (16)

Для амплитудного и действующего значений переменного тока справедлив закон Ома:

, (17)

, (18)

, (19)

где величина R называется полным сопротивлением цепи переменного тока.

Количество теплоты Q, выделяющееся на активном сопротивлении, вычисляется по закону Джоуля-Ленца:

. (20)

Величина преобразованной электрической энергии в другие виды энергии определяется мощностью переменного тока. Так как - сила тока и напряжение - переменные величины, то и мощность в цепи переменного тока является переменной величиной. Поэтому имеет смысл говорить только о мгновенном значении мощности P=I2 Ra, или о среднем значении мощности период Т изменения переменного тока, вычисляемой по формуле:

. (21)

Мощность называют активной мощностью. Множитель cosφ называют коэффициентом мощности, где: j - сдвиг по фазе между колебаниями силы тока и напряжения. Коэффициент мощности вычисляется по формуле:

. (22)

Для преобразования переменного тока одного напряжения в переменный ток другого напряжения при той же частоте используют устройство, называемое трансформатором. Трансформатор представляет собой систему, состоящую из двух обмоток (катушек), связанных одним сердечником. Если первоначально катушка содержит N1 витков, а вторичная - N2 витков, то коэффициент трансформации k вычисляется по формуле:

, (23)

где e1 и e2 - э.д.с. индукции в первичной и вторичной обмотках.

Если падение напряжения на активном сопротивлении первичной обмотки трансформатора ничтожно мало, то: ε1 = u1 и ε2 = u2. Тогда:

, (24)

где U1 и U2 - напряжение на первичной и вторичной обмотках трансформатора.

К.п.д. трансформатора называют отношение мощности Р2, отдаваемой вторичной обмоткой, к мощности Р1, подводимой к первичной обмотке:

. (25)

К.п.д. современных трансформаторов очень высок - 97-98 %. Поэтому по закону сохранения энергии мощность тока в первичной обмотке практически равна мощности тока во вторичной обмотке: Р1 Р2. Отсюда следует, что: J1U1 J2U2.

Тогда формулу (24) можно записать в виде:

, (26)

где: J1, J01 - действующее и амплитудное значения тока в первичной обмотке;

J2, J02 -действующее и амплитудное значения тока во вторичной обмотке.

23. электромагнитные волны

1. Существуют электромагнитные волны, то есть распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы и перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис. 2.6.3).

Рисунок 2.6.3. Синусоидальная (гармоническая) электромагнитная волна. Векторы , и взаимно перпендикулярны

2. Электромагнитные волны распространяются в веществе с конечной скоростью

Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные: ε₀ = 8,85419·10^–12 Ф/м, μ₀ = 1,25664·10^–6 Гн/м.

Длина волны λ в синусоидальной волне свявзана со скоростью υ распространения волны соотношением λ = υ T = υ / f, где f – частота колебаний электромагнитного поля, T = 1 / f.

Скорость электромагнитных волн в вакууме (ε = μ = 1):

Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.

Вывод Максвелла о конечной скорости распространения электромагнитных волн находился в противоречии с принятой в то время теорией дальнодействия, в которой скорость распространения электрического и магнитного полей принималась бесконечно большой. Поэтому теорию Максвелла называют теорией близкодействия.

3. В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Поэтому объемные плотности электрической и магнитной энергии равны друг другу: w _э = w _м.

Отсюда следует, что в электромагнитной волне модули индукции магнитного поля и напряженности электрического поля в каждой точке пространства связаны соотношением

4. Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Если выделить площадку S (рис. 2.6.3), ориентированную перпендикулярно направлению распространения волны, то за малое время Δ t через площадку протечет энергия Δ W _эм, равная

Δ W эм = (w э + w м)υ S Δ t.

Плотностью потока или интенсивностью I называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади:

Подставляя сюда выражения для w _э, w _м и υ, можно получить:

Поток энергии в электромагнитной волне можно задавать с помощью вектора направление которого совпадает с направлением распространения волны, а модуль равен EB / μμ₀. Этот вектор называют вектором Пойнтинга.

В синусоидальной (гармонической) волне в вакууме среднее значение I _ср плотности потока электромагнитной энергии равно

где E ₀ – амплитуда колебаний напряженности электрического поля.

Плотность потока энергии в СИ измеряется в ваттах на квадратный метр (Вт/м²).

24.Существование электромагнитных волн было теоретически предсказано великим английским физиком Дж. Максвеллом в 1864 году. Максвелл проанализировал все известные к тому времени законы электродинамики и сделал попытку применить их к изменяющимся во времени электрическому и магнитному полям. Он обратил внимание на ассиметрию взаимосвязи между электрическими и магнитными явлениями.Максвелл ввел в физику понятие вихревого электрического поля и предложил новую трактовку закона электромагнитной индукции, открытой Фарадеем в 1831 г.: Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты. Максвелл высказал гипотезу о существовании и обратного процесса: Изменяющееся во времени электрическое поле порождает в окружающем пространстве магнитное поле. Гипотеза Максвелла была лишь теоретическим предположением, не имеющим экспериментального подтверждения, однако на ее основе Максвеллу удалось записать непротиворечивую систему уравнений, описывающих взаимные превращения электрического и магнитного полей, то есть систему уравнений электромагнитного поля (уравнений Максвелла). Из теории Максвелла вытекает ряд важных выводов: 1. Существуют электромагнитные волны, то есть распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы и перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис. 5.6.3).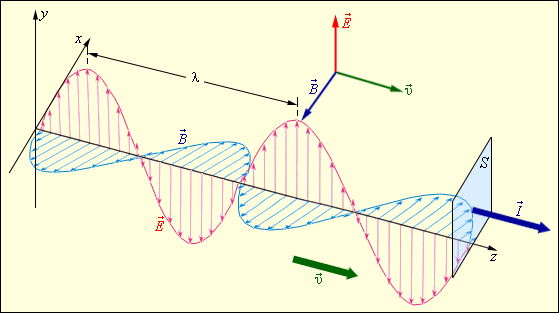

2. Электромагнитные волны распространяются в веществе с конечной скоростью Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м. Скорость электромагнитных волн в вакууме (ε = μ = 1):

Открытие радиоволн дало человечеству массу возможностей. Среди них: радио, телевидение, радары, радиотелескопы и беспроводные средства связи. Всё это облегчало нам жизнь. С помощью радио люди всегда могут попросить помощи у спасателей, корабли и самолёты подать сигнал бедствия, и можно узнать происходящие события в мире.
Создание электромагнитных волн опытным путём принадлежит физику Герцу. Для этого Герц использовал высокочастотный искровой разрядник (Вибратор). Произвёл этот опыт Герц в 1888 г. Состоял вибратор из двух стержней, разделённых искровым промежутком. Экспериментировал Герц с волнами частотой 100000000 Гц. Вычислив собственную частоту электромагнитных колебаний вибратора, Герц смог определить скорость электромагнитной волны по формуле υ=λν.Она оказалась приближенно равна скорости света: с=300000 км/с.