Загальні положення. Національний університет "Львівська політехніка"

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Національний університет "Львівська політехніка"

Навчально-науковий Інститут підприємництва та перспективних технологій

Кафедра фінансів

"Актуарна математика"

Методичні рекомендації до виконання

Індивідуальної роботи

для студентів освітньо-кваліфікаційного рівня «бакалавр» напряму підготовки "Фінанси і кредит"

Львів – 2014

Методичні рекомендації до виконання індивідуальної роботи

розробив доц.,к.фіз.-мат.н. Волошин В.В.

Затверджено на засіданні

кафедри фінансів

Протокол №__ від _________ 2014 р.

Зав. каф. к.е.н., доц. П.А. Гориславець

Завдання для виконання індивідуальної роботи

з дисципліни «актуарна математика»

Загальні положення

1.1. Мета та завдання індивідуальної роботи

Метою індивідуальної роботи з дисципліни «Актуарна математика», є закріплення та систематизування знань студентами по даній дисципліні, та набуття практичних навиків у актуарних розрахунках.

Завдання індивідуальної роботи з дисципліни «Актуарна математика» полягає в наступному:

1. засвоєння теоретичних знань з дисципліни «Актуарна математика», а саме: змісту та основних понять актуарних розрахунків, способів і методів розподілу тривалості життя, особливості моделей страхування життя, страхуання аннуїтетами, зміст чистих премій, декрементів.

2. на основі засвоєних теоретичних знань набути практичних навиків виконання актуарних розрахунків, а саме:

-.розрахування чистої теперішньої вартості грошей;

- розрахування розподілу тривалості життя;

- розрахування сили смертності;

Індивідуальна робота є складовою самостійної роботи студента.

Індивідуальна робота складається з 20 задач, кожна з яких оцінюється по 3 бали.

1.2 Вимоги до написання індивідуальної роботи

Індивідуальна робота повинна бути написана студентом згідно з затвердженим варіантом. Номер варіанта вибирається відповідно до порядкового номера студента у списку навчальної роботи. При написанні індивідуальної роботи студентові слід використовувати і відображати в цій роботі методику актуарних розрахунків, а саме: слід навести формули, які є базовими для визначення тих чи інших показників; вказати зміст компонентів цих формул; детально описати порядок розрахунків, вказавши, одиниці виміру, що визначаються. В кінці роботи наводиться список використаної літератури, складений відповідно до загальноприйнятих бібліографічних вимог.

Обсяг індивідуальної роботи індивідуальної роботи визначається потребами повного відображення проведених розрахунків із врахуванням висновків щодо написаної індивідуальної.

Завдання для виконання контрольної роботи студента.

(Вибір варіанта n проводиться відповідно до порядкового номера студента у журналі академічної групи)

Задача 1.

Функція розподілу ймовірності для часу майбутнього життя людини описується законом де Муавра з віком максимального життя 110 років. Визначити:

1. ймовірність того, що людина віком (40+2n) років помре протягом наступних 7 років

2. ймовірність того, що людина віком (45+n) років не помре протягом наступних 13 років

3. силу смертності людини віком (60-n) років при досягненні віку 95 років.

Задача 2.

Використовуючи таблиці смертності, визначити:

1. ймовірність того, що людина віком (20+2n) років помре протягом наступних 7 років

2. ймовірність того, що людина віком (45+n) років не помре протягом наступних 13 років

Задача 3.

На рахунок покладено суму 2700 грн на термін 6років. Визначити суму виплати інвестору після закриття рахунку при відсотковій ставці (n+3)%:

1. за правилом простих відсотків

2. за правилом складних відсотків

Задача 4.

Обчислити дисконтний множник при відсотковій ставці (n+3)%.

Задача 5.

Обчислити чисту премію та варіацію при терміновому страхуванні, страхуванні на чисте дожиття і страхуванні на дожиття людини віком (15+n) років на 5 років при відсотковій ставці (3+n)% з виплатою 1500 грн.

Задача 6.

Відомо, що , . Обчислити .

Задача 7.

Відомо, що , 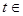[0,85). Обчислити .

Задача 8.

При відсотковій ставці (3+n)% знайдіть ,

Задача 9.

Інвестор вкладає х +1000 грн. на 5 років. Знайдіть акумульовану суму, якщо х співпадає з номером варіанта:

а) при річній ставці 10%;

б) конвертації піврічній 10%;

в) конвертації щомісячній 10%.

Задача 10.

Який внесок зробив вкладник, якщо після закінчення 5 років він при і % (і співпадає з номером варіанта) прибутковості перетворився в 638 грн. 13 коп.?

Задача 11.

Відомо, що s(x) – функція виживання, що показує, яка частина новонароджених жива на момент часу x,

а) відсоткова ставка і співпадає з номером варіанта;

б) - стала, [0,100].

Обчислити .

Задача 12

Визначити розмір внеску в пенсійний фонд, якщо через рік щорічно протягом 10 років виплачується пенсія 1500 грн. Ефективна річна відсоткова ставка і співпадає з номером варіанта.

Задача 13

Банком видана позичка 20000 грн. на 5 років під річну відсоткову ставку і (співпадає з номером варіанта). Погашення позички здійснюється наприкінці кожного оку однаковими виплатами. Визначити розмір виплат.

Задача 14

Клієнт купує 10-річну ренту з виплатою 1500 грн. наприкінці кожного року. При цьому передбачається, що річна відсоткова ставка протягом найближчих 5 років дорівнює і % (і співпадає з номером варіанта), в інші роки - 6 %. Визначити розмір ренти.

Задача 15

Яким повинен бути внесок у пенсійний фонд, якщо пенсія буде виплачуватися протягом 10 років по 1500 грн. щорічно. Перша виплата через рік. Ефективна ставка і % річних (і співпадає з номером варіанта).

Задача 16

Надається позика 20000 грн. на 5 років під і % річних (і співпадає з номером варіанта), погашення наприкінці року. Знайдіть суму щорічної виплати.

Задача 17

При ставці і=7% річних, використовуючи таблицю смертності, обчислити (х співпадає з номером варіанта): 1) 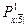; 2) ; 3) .

Задача 18

Нехай кількість осіб, які дожили до віку х (з розрахунку на 100 осіб) обчислюється , . Відсоткова ставка і співпадає з номером варіанта. Обчислити:

а) б)

Задача 19

Розглядається терміновий контракт страхування життя людини х (х співпадає з номером варіанта). Застрахована сума 5000 грн., яка виплачується наприкінці року смерті; термін страхування 6 років; відсоткова ставка і співпадає з номером варіанта; смертність відповідає закону Де Муавра з кінцевим віком . Знайти чисту річну премію, яка виплачується щорічно на початку року, поки людина жива, але не більше 6 років.

Задача 20

Нехай і =10%, а смертність відповідає закону Де Муавра з кінцевим віком . Заповнити таблицю (х співпадає з номером варіанта).